前回までで、微分、偏微分、最小二乗法、ベクトル、行列までを書いてきました。
今回は、今までの知識を総動員し、ベクトルと行列による微分について書いていきます。ここまでの内容は、かの有名なディープラーニングにも使われています!
今回の目的は以下になります。
- 回帰モデルをベクトルと行列を使って表現できる。
- ベクトルや行列の式変形に慣れる。
- ベクトルを使った微分を理解する。
誰が読んでも理解できることを目指していますので、分かりにくい、理解できない等ありましたら、お気軽にコメント頂けると幸いです。なお、RやPythonを使わなくても、学ぶことができる内容ですので、数学の知識だけ学びたいという方も是非ご覧ください(^^)
行列を使って回帰モデルを表す。
さて前回までの記事で、ベクトル・行列は"たくさんある式をコンパクトにまとめられる"ことがメリットであると書きました。前回の記事で偏微分を使って作成した回帰モデルですが、ベクトルと行列を使うことで、コンパクトに、スマートに、回帰モデルを作成できます。
前回同様に、メール数と売上データを使います。こんなデータでした。
| sales | |
|---|---|
| 1 | 12500 |
| 2 | 19700 |
| 3 | 29600 |
| 4 | 53700 |
| 5 | 47700 |
| 6 | 75200 |
| 7 | 54500 |
| 8 | 85800 |
| 9 | 91200 |
| 10 | 102200 |
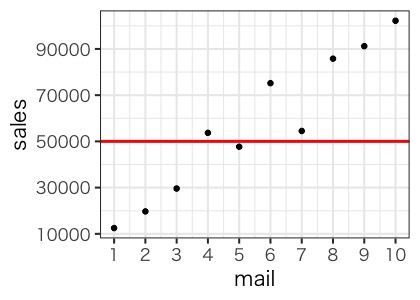
このmailを、salesを
、線形モデルの切片は
、傾きを
として、それぞれベクトルと行列で表現してみます。以前の記事で補足として書いた誤差を使った表し方です。

ここでも横×縦の考え方です。メールの数であるxは、すべて1のベクトルをくわえることで、2行10列の行列となり、係数ベクトルとのかけ算を可能にし、切片係数の
を式の中に加えることができます。一種のお作法のようなものですね(^^;)
上記の式を展開してみると、
となって、全部で10この式が、1行にまとめられていることがわかります。
行列を使って誤差の平方和を表す。
さて、ここから誤差を最小にするためには、誤差の平方和を最小にする必要がありますが(最小二乗法)、誤差はベクトルとなっていて二乗することができません。そこで、転置をした同じ誤差ベクトルとの内積を求めます。(前回まででやったように、ベクトルや行列のかけ算は内積でしたね。)
ここから行列における以下の二つのルールを用いて式変形を行います。
1.スカラーは転置しても値は同じ
2.行列の内積の転置はそれぞれを転置して順番を逆にする。
と確かに同じになっていることが分かります。このルールを式に適応してみると、はスカラーになるので、
と変形できます。すると
となります。これで誤差の平方和を行列で表すことができました。
ベクトルとベクトルの微分
さて、前回の記事で、最小二乗法を解くために偏微分を使いました。今回も微分を使って、誤差が最小となる値を求めるのですが、ここでベクトルや行列で微分をすると、一気に値を求めることができます。先ほどの式をを要素としてもつベクトル
で微分してみます。微分は、足してから微分しても、微分してから足しても同じという性質を使うと以下のようになります。
は
と関係ないので、微分によって消えます。次の項についてですが、これがベクトルをベクトルで微分する項になります。まずは
の項からみていきましょう。ここでも微分の性質である、かけてから微分しても、微分してからかけても同じという性質を使って、
の微分を考えていきます。は10行1列のベクトルです。
これをベクトルであるで微分すると、以下のようなイメージになります。

ポイントは、ベクトルをベクトルで微分すると行列になるところです。これが分かれば、あとは偏微分するだけなので、
となっていきます。ここで注目して欲しいのが、
となる点です。例えば、ベクトルではなく、スカラーの微分では、
となりますよね。これはベクトルの微分でも同じように適応できるところがポイントです。
二次形式の微分
さて、次に
を計算してみましょう。実は上記の微分は二次形式の微分という公式を用いることができます。その公式前に二次形式について紹介していきましょう。
二次形式とは、
- 変数の二次の項のみからなる式
の形に変換できる。
という特徴を持っています。例えば、こんな式です。
上記の式の中にある項は全て、、
の二次の項からなっていますね。これを以下のように変形してみます。
これはまさしく、の形になっていますね!実は、式が2次形式の形であればどんな式でも上記の形に変形することができます。ここで、最初の式をベクトルで微分したらどうなるでしょうか?ポイントは、スカラーをベクトルで微分するとベクトルになるということです。やってみましょう。
となります。つまり、
です。これが二次形式の微分の公式です。これは、
となるような二乗微分のベクトル版とも言えますね。

この公式を使うと
と変形することができます。これは、を計算してみると対称行列になることを利用しています。
正規方程式から回帰モデルのパラメーターを求める。
さて、これで準備が整いました。式を整理してみましょう。
最小二乗法で学んだように、微分した結果が0になるところが最小となる値となるので、
を解けば回帰モデルのパラメーターを求めることができます。この一番したの式を正規方程式とよび、多くの参考書等でいきなり出てくることがありますが、導出方法は上記の通りです!
あとは前回行列の回で扱った逆行列の知識を使えば、正規方程式を解くことができます。
これで回帰モデルは、
と求めることができます。
RとPythonによる実践
最後に実際にRとPythonを使って正規方程式をとき、を計算してみましょう。
#データの作成 mail <- seq(1,10) sales <- c(12500,19700,29600,53700,47700,75200,54500,85800,91200,102200) y <- sales X <- matrix(c(rep(1, 10), mail),ncol = 2) #正規方程式をとく beta <- solve(t(X) %*% X) %*% t(X) %*% y print(beta) > [,1] [1,] 3253.333 [2,] 9810.303
#データの生成 mail = np.arange(1,11) sales = np.array([12500,19700,29600,53700,47700,75200,54500,85800,91200,102200]) X = np.zeros((10,2)) X[:,0] = 1 X[:,1] = mail y = sales #正規方程式を解く inv_XTX = np.linalg.inv(np.dot(X.T, X)) beta = np.dot(np.dot(inv_XTX, X.T),y) print(beta) >[3253.33333333 9810.3030303 ]
まとめ
ベクトルを使った微分は、データサイエンスの中でも肝となる部分で、逆にここをしっかりと理解することで、基礎的な統計学からディープラーニング を始めとする機械学習手法まで、幅広く理解することができます。最後に本記事のポイントをまとめてみます。
- 回帰式は
と表すことができる。
スカラーは転置しても値は同じ
行列の内積の転置はそれぞれを転置して順番を逆にする。
スカラーをベクトルで微分するとベクトルに、ベクトルをベクトルで微分すると行列になる。
変数の二次の項のみからなる式を二次形式と呼ぶ。
正規方程式を解くことで、回帰モデルのパラメーターを求めることができる。
※本記事は筆者が個人的に学んだことをまとめた記事になります。所属する組織の意見・見解とは無関係です。また、数学の記法や詳細な理論、用語等で誤りがあった際はご指摘頂けると幸いです。
参考
データサイエンスで必要となる数学がほとんど網羅されています。初めての方には、少し難易度が高いですが、数式の導出など丁寧にまとめてあり、脱初心者を目指す方にはとてもおすすめです。
データサイエンスを学び始めて右も左も分からなかったときこの本に出会い、”統計、機械学習を学ぶための数学を学ぶ本”というコンセプトがぴったりで感動した。今、読み直してみるとさらに理解が深まり、データサイエンス数学入門書としては間違いなくおすすめです。
![統計学が最強の学問である[数学編]――データ分析と機械学習のための新しい教科書 統計学が最強の学問である[数学編]――データ分析と機械学習のための新しい教科書](https://m.media-amazon.com/images/I/51p4aPUyeOL._SL160_.jpg)
統計学が最強の学問である[数学編]――データ分析と機械学習のための新しい教科書
- 作者:西内 啓
- 発売日: 2017/12/21
- メディア: 単行本(ソフトカバー)
最適化となっていますが、第一章の数学基礎は、具体例とともにすごく分かりやすくまとまっています。本記事を書くにあたり、二次形式の部分は本書を参考にしました。

- 作者:健一, 金谷
- 発売日: 2005/09/01
- メディア: 単行本
正規方程式の導出で、参考にさせて頂きました。
