第7回：RとPythonで1から学ぶデータサイエンス数学~確率分布・確率変数と積分~

確率分布と積分は、統計学を知る上では欠かせない数学知識です。今回は確率分布と確率変数の基本と、積分の関係性についてご説明していきます。

今回の目的は以下になります。

確率分布、確率変数とは何かを理解する。
確率質量関数、確率密度関数の違いを理解する。
積分を使って、確率密度関数から確率と平均値を求めることができる。

誰が読んでも理解できることを目指していますので、分かりにくい、理解できない等ありましたら、お気軽にコメント頂けると幸いです。なお、RやPythonを使わなくても、学ぶことができる内容ですので、数学の知識だけ学びたいという方も是非ご覧ください（^^）

確率変数と確率分布
- 偏ったサイコロの確率
- ルーレットの確率：積分を使って
積分と平均値
まとめ
参考

確率変数と確率分布

確率については、おそらく馴染み深い数学だと思います。日常的にも、無意識のうちに確率の概念を利用しているのではないでしょうか？データサイエンスで、よく用いられる確率には、データが得られると想定される確率の分布である確率分布の概念です。確率分布の基本的な概念は、他の記事でもご紹介したので、こちらを先に読まれるとより理解しやすいかもしれません。

www.medi-08-data-06.work

偏ったサイコロの確率

一般的なサイコロは、どの目も同じ確率がでることが想定されています。つまり、1~6の目が出る確率は、一様に1/6です。これを、横軸を出る目の数、縦軸をその目が出る確率としてみると、こんなグラフになります。

データサイエンス数学

どの目も1/6の確率で得られることを表しています。これがすでに確率分布です。確率分布とはズバリ物事の起こりやすさを表したものと理解しましょう。特に統計学では、手元にあるデータが、何らかの確率分布から得られていると想定します。つまり、サイコロの目は、この確率分布に従って、生成されているイメージです。そして、得られる可能性のある全てのデータの集合を確率変数と呼びます。サイコロでは1から6の目が確率変数です。

データサイエンス数学

ここから普通のサイコロを例にしては味気ないので、出る目の数が大きくなるほど、その目が出る確率が高いくなる特殊なサイコロを考えてみます。このサイコロの確率分布はこんな感じになります。

データサイエンス数学

ここでのポイントは、確率変数が得られる確率を全て足すと1になることです。サイコロを振って1から6までのどれかが出る確率は1ですからね。このサイコロの確率分布を、入力値が確率変数、出力値が確率となる関数にしてみます。例えば、この関数に4を入力すると、4がでる確率4/21が出力されます。関数の考え方に馴染みのない方には、第二回の記事を

www.medi-08-data-06.work

このように確率変数を入力すると、確率が出力される関数のことを確率質量関数いいます。名前は"いかつい"ですが、確率が出力されるただの関数ですので、安心してください。この確率質量関数をsaikoro関数と呼ぶことにしましょう。そして第一回同様に、それぞれの目が出る確率を $p$ で表します。例えば、1が出る確率は

$p(1) = saikoro(1) = \dfrac{1}{21}$

です。

データサイエンス数学

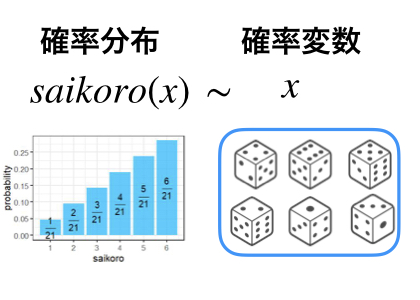
上記のように確率変数がある確率分布に従っているということを”にょろにょろ”を使って表現することがよくあるので、覚えておきましょう。上のスライドでは、saikoro関数という確率分布に従って、サイコロの目xが出現することを表しています。

統計学では、様々な事象を様々な確率分布に当てはめて事象の推論を行います。例えば、地震はポワソン分布という分布という確率分布に従って発生していると仮定すると、これから～～年の間に地震が起こる確率は～～％であると推定することができます。しかし、分布はあくまで仮定であって、真の事象が起こる分布は誰にも分からないというのが統計学の”きも”になるので、補足程度に覚えておいてください。

www.medi-08-data-06.work

さて少し話がそれましたが、ここでサイコロの目が4以下になる確率を求めてみます。4以下ということは、1，2，3，4の目のうちのどれかがでる確率ですので、

$p(1)+p(2)+p(3)+p(4) \\ = saikoro(1)+saikoro(2)+saikoro(3)+saikoro(4)\\ =\dfrac{1}{21}+\dfrac{2}{21}+\dfrac{3}{21}+\dfrac{4}{21}\\ = \dfrac{10}{21} \fallingdotseq 0.48$

となって、48％ぐらいの確率ですね。この上記の式はシグマの記号を使って、

$\sum_{i=1}^{4} p(x_{i})\\ =\sum_{i=1}^{4} saikoro(x_{i})\$

と表すこともできます。

#サイコロの目がでる確率が出力される関数
saikoro <- function(x){
  return(x/21)
}
# 1が出る確率
print(saikoro(1))
>[1] 0.04761905

# 4以下の目がでる確率
num <- c(1,2,3,4)
print(sum(saikoro(num)))
>[1] 0.4761905

#サイコロの目がでる確率が出力される関数
def saikoro(x):
    return(x/21)

# 1が出る確率
print(saikoro(1))
>0.047619047619047616
# 4以下の目がでる確率
num = np.array([1,2,3,4])
print(np.sum(saikoro(num)))
>0.47619047619047616

ルーレットの確率：積分を使って

次に、1から20で一周するルーレットを考えてみます。

データサイエンス数学

このルーレットを回して5以下の数が出る確率を求めてみます。先ほど同様に

$1が出る確率+2が出る確率\cdots +5が出る確率\\ =p(1)+p(2)\cdots+p(5)$

とすれば求まりそうですが、ルーレットは数字と数字の間を滑らかにうごくため、1と2の間に止まる可能性もあります。また、5が出たと思っても、厳密には5.1かもしれないし、4.99999かもしれません。このようにルーレットの場合は、一つの数字がでる確率を求めることが出来ません。が、すべての確率変数が出る確率を足すと1になることは分かっています。この条件から、ある確率変数が出る確率を直接求めるのをあきらめて、他の確率変数と比べた時の相対的な出やすさを高さにした確率分布にしてしまいます。まずは、ルーレットの確率分布を図にしてみましょう。

データサイエンス数学

0未満、もしくは20より大きい数はルーレットには存在しないので、確率は0になっています。そして、0から20の間ですが、高さが0.05になっていますよね。これは、面積が1になるという条件から、導き出した値です。ここで、間違えやすいポイントですが、この0.05という数字は確率ではなく、相対的な出やすさであることです。つまり、0から20の間のどの数字も同じ出やすさであることを表しています。この相対的出やすさのことを確率密度と呼び、四角の面積が確率となります。例えば、すべての数字がでる確率は、

$20\times 0.05=1$

ですし、5以下の数字が出る確率は、

$5\times 0.05=0.25$

と求めることができます。入力xの値を変化させて、それぞれの確率をアニメーションにしてみました。

データサイエンス数学

このように、確率変数を入力すると、その値の確率密度（相対的な出やすさ）が出力され、関数の面積が確率となる関数を確率密度関数と呼びます。

今回はこの確率密度関数をroulette関数と呼ぶことにします。このルーレットでは、確率密度関数が四角形になったので、底辺×高さで確率を求めることができました。しかし、多くの確率密度関数はぐにゃぐにゃと曲がった形をしています。ここで登場するのが積分です。実際にroullet関数を使って5以下の数字が出る確率を積分を使って求めてみます。積分の基本的な考え方は、とても小さい幅の底辺、確率密度を高さとした長方形を足し合わせてるイメージです。

データサイエンス数学

こうすることで、確率密度関数が曲線になっても面積を求めることができます。この小さい幅をdxで表し、5以下の数字が出る確率を積分を使って数式で表すと

$\int_{0}^{5} roulette(x) dx$

です。積分の計算の流れは、

微分したら、積分したい関数となるような関数を見つける。
その関数に上の数字を入れた値から、下の数字を入れた値を引く。

です。今回のroulette関数は0から20の間では、出力は0.05なので、y=0.05という関数になります。よく分からないと思いますの、実際に積分をしてみると

データサイエンス数学

0.25と同じ結果になりましたね。重要なのでここでもう一度、確率分布の種類はたくさんありますが、確率変数を入力すると、その確認もしくは確率密度が出力される関数であることを意識しておけば、怖くありません。

積分を行うには、Rではintegrate、pythonではscipy.integrate.quadを使います。それぞれ関数の定義の仕方にクセがあるので注意してください。

#ルーレット関数を定義
#結果はベクトルで返す必要あるので、中で繰り返し処理をする
roulette <- function(num){
  ans <- c()
  for(n in num){
    if(n>=0&n<=20){
      ans <- c(ans,0.05)
    }else{
      ans <- c(ans,00)
    }
  }
  return(ans)
}

#積分（0から5の範囲で）
#結果は、積分値の近似値と誤差
print(integrate(roulette,0,5))
>0.25 with absolute error < 2.8e-15

from scipy import integrate
#ルーレット関数を定義
#結果はベクトルで返す必要あるので、np.whereで条件を指定する
def roulette(num):
    ans = np.where((num>=0)&(num<=20),0.05,0)
    return(ans)

#積分（0から5の範囲で）
#結果は、積分値の近似値と誤差
print(integrate.quad(roulette, 0, 5))
>(0.25000000000000006, 2.775557561562892e-15)

積分と平均値

積分の最後に、積分を使って平均値を算出する方法をご紹介します。平均値は

$E(x)=\sum_{i=1}^{n} x_{i}p(x_{i})$

の期待値の形で表すことができました。

www.medi-08-data-06.work

今回学んだ用語で言い換えると

$確率変数\times 確率$

を足し合わせたものです。これを使って偏ったサイコロの平均値を求めてみてみると、

$\sum_{i=0}^{6} x_{i}p(x_{i})\\ =1\times saikoro(1)+2\times saikoro(2)\cdots +6\times saikoro(6)\\ = 4.33....$

となります。この考え方を使うと積分でも平均値を算出することができます。

$\int_{0}^{20} xp(x) dx\\ = \int_{0}^{20} x\,roulette(x) dx$

これを計算するためには、部分積分法を使いますが、よく分からないという方は、確率分布の平均値が上記の式で表されるということだけでも覚えておいてください。実際に計算してみます。

【部分積分法】公式や証明のコツを解説!例題を使った覚え方 | Studyplus（スタディプラス）

$\int_{0}^{20} x\,roulette(x) dx \\ = \int_{0}^{20} x\,(0.05x)' dx\\ = \left[0.05x^{2}\right]_0^{20}-\int_{0}^{20}1\times\,0.05x dx\\ =0.05\times 400 - \left[0.025x^{2}\right]_0^{20}\\ = 10$

もちろん平均値は真ん中の10ですね。このように確率密度関数の平均値を積分を使って求める方法は頻出なので覚えておきましょう。確率密度関数についてさらに知りたい方は、以下の記事をご覧ください。

www.medi-08-data-06.work

#サイコロの平均値
num <-c(1,2,3,4,5,6)
print(sum(num*saikoro(num)))
[1] 4.333333

#ルーレットの平均値
#x*roulette(x)の関数を作る
f <- function(x) {
  return(x*roulette(x))
}
#0~20の範囲で積分
print(integrate(f,0,20))
>10 with absolute error < 1.1e-13

#サイコロの平均値
num = np.array([1,2,3,4,5,6])
print(np.sum(num*saikoro(num)))
>4.333333

#ルーレットの平均値
#x*roulette(x)の関数を作る
def f(x):
    return x*roulette(x)
    #0~20の範囲で積分
print(integrate.quad(f,0,20))
>(10.0, 1.1102230246251565e-13)