ディープラーニングは言わずもがな、機械学習の世界では名実ともにエースと呼んでいいほど有名なアルゴリズムです。人間の脳を模倣していると聞くと、なんだかSFの世界を想像しますが、実は案外簡単なアルゴリズムで成り立っています。
今回は、そんなディープラーニングを出来るだけシンプルに、そして具体的にPythonとRで実装しながら理解を深めていきます。なお、今回の内容はこちらの書籍を参考にしています。

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
- 作者:斎藤 康毅
- 発売日: 2016/09/24
- メディア: 単行本(ソフトカバー)
なお、式のベクトルや行列表記に馴染みのない方は、そちらを解説した記事もありますので、ご参照ください。
ディープラーニング風ロジスティック回帰モデル
ディープラーニングが最も活躍するのは、画像認識、言語処理など、ある情報を入れるとそれが何であるかを判別するクラス分類です。クラス分類を扱える機械学習アルゴリズムはいくつかありますが、ディープラーニングは何がすごいのでしょうか?以前書いたロジスティック回帰モデルと比較をしてみましょう。
ここで今後のディープラーニングの理解のため、ロジスティック回帰モデルを以下のように表してみます。
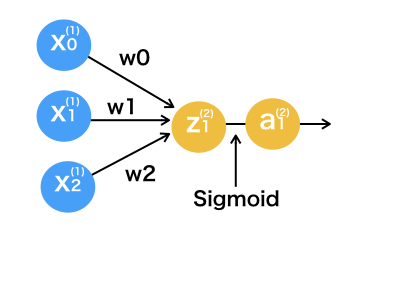
見なれるまでは少し混乱するかもしれませんが、表していることは単純です。変数の肩に乗っているかっこの中の数字は、ディープラーニング で言うところの層の番号を表しています。まず、1層目の変数x0=1とx1、x2の情報をw0、w1、w2を使って線形結合し、とします。
w1とw2はロジスティック回帰モデルで言うところの係数、w0は切片です。そして2層目のをシグモイド関数(ロジスティック関数)で確率へ変換し、
を作ります。
ロジスティック回帰モデルでは、このが0.5以上の時にクラス1、そうでなかったらクラス2に分類するモデルでした。ちなみにこのシグモイド関数のような線型結合したものを変換する関数を、活性化関数(アクティベーション)、wのような係数を重み、切片に対応する重みをバイアス、一つ一つの丸(x1やz2など)をニューロンと呼びます。文字の右肩に乗っているかっこの数字は、ディープラーニングの層を表しています。
つまりロジスティック回帰モデルとは、一層目のニューロンを線型結合して、二層目でシグモイド関数によって値を変換し、出力するという二層のディープラーニングモデルで表すことができます。
ロジスティック回帰モデルをディープラーニング 風にして、見るからに非線形なこんな分類問題を解いてみましょう。まずはデータを作成します。
import numpy as np import matplotlib.pyplot as plt % matplotlib inline x1_0 = np.array([np.random.normal(size=50,loc=2,scale=1), np.random.normal(size=50,loc=-2,scale=1), np.random.normal(size=50,loc=2,scale=1)]).reshape(150,1) x2_0 = np.array([np.random.normal(size=50,loc=-2,scale=1), np.random.normal(size=50,loc=2,scale=1), np.random.normal(size=50,loc=2,scale=1)]).reshape(150,1) x1_1 = np.array([ np.random.normal(size=150,loc=-1,scale=1)]).reshape(150,1) x2_1 = np.array([ np.random.normal(size=150,loc=-1,scale=1)]).reshape(150,1) X = np.c_[np.r_[x1_0,x1_1],np.r_[x2_0,x2_1]] y = np.repeat([0,1],[150,150]) #データをシャッフル p=np.random.permutation(300) X = X[p,:] y = y[p] #可視化 plt.scatter(x1_0,x2_0,color="y",label="0") plt.scatter(x1_1,x2_1,color="green",label="1") plt.xlabel("x1",size=15) plt.ylabel("x2",size=15) plt.tick_params(labelsize=18) plt.legend(loc='upper left',fontsize=15)
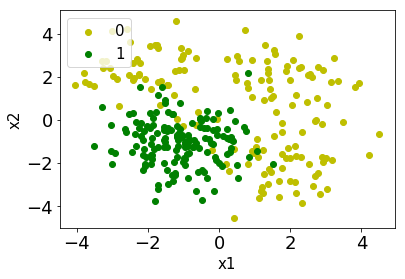
次にシグモイド関数と上記のディープラーニング を実装していきます。ディープラーニング では、入力から出力までの一連の流れをフォワードプロパゲーション(Forward-propagation)と呼びます。
#ロジスティック回帰 def sigmoid(x): return 1/(1+(np.exp(-x))) #フォワードプラバゲーション関数 def forward(W_1,W0_1,X): #1層目 z_1 = np.dot(X,W_1)+W0_1 #活性化 a_1 = sigmoid(z_1) return a_1
最後は重みですが、前回はこの重みを最急降下法を使って求めましたが、ディープラーニング ではバックプロパゲーション(Back-propagation)というかっこいい名前のアルゴリズムで求めるのですが、それはまた次回にして、今回は既に分かっているものとします。
W_1 = np.array([-0.95,-0.88]) W0_1 = -0.56
準備ができました。試しに1サンプル目を選んで、流してみましょう。
print(X[1:2,:]) >>[-2.9969286 4.14473662]]#(1行2列) print("1サンプル目の出力 {}".format(forward(W_1,W0_1,X[1:2,:]))) >>1サンプル目の出力 [0.20419381]
出ました。クラス1になる確率は20%程度なので、1サンプル目はクラス0に分類されそうです。(データ生成過程とシャッフルによって、この値は異なることがあります。)この調子で全てのサンプルを予測して、決定境界を描いてみます。 確率を受け取ってクラスを返すpredict関数も定義しておきましょう。
#予測関数の定義 def predict(x): if x>=0.5: return 1 else: return 0 #決定境界のプロット x1_min, x1_max = X[:, 0].min()-1, X[:, 0].max()+1 x2_min, x2_max = X[:, 1].min()-1, X[:, 1].max()+1 x1_mesh, x2_mesh = np.meshgrid(np.arange(x1_min, x1_max, 0.05), np.arange(x2_min, x2_max, 0.05)) X_mesh = np.array([x1_mesh.ravel(), x2_mesh.ravel()]).T y_mesh = np.array(list(map(predict,forward(W_1,W0_1,X_mesh)))) y_mesh = y_mesh.reshape(x1_mesh.shape) plt.contourf(x1_mesh, x2_mesh, y_mesh, alpha=0.4,cmap="Greens") plt.xlim(x1_mesh.min(), x1_mesh.max()) plt.ylim(x2_mesh.min(), x2_mesh.max()) plt.scatter(x1_0,x2_0,color="y",label="0") plt.scatter(x1_1,x2_1,color="green",label="1") plt.xlabel("x1",size=15) plt.ylabel("x2",size=15) plt.tick_params(labelsize=18) plt.legend(loc='upper left',fontsize=15) plt.show()
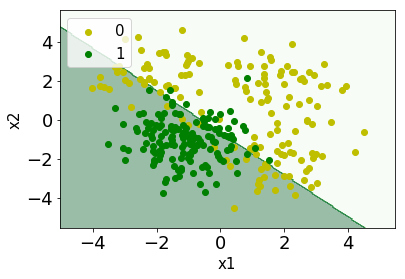
やはりロジスティック回帰モデルは線形分類になりますね。この時の正解率は
pred = list(map(predict,forward(W_1,W0_1,X))) print("accuracy {:.2f}".format(sum(pred==y)/len(y))) >>accuracy 0.80
80%程度の正解率ですね。しかし、見るからに線形的に分離しようとすると、無理がありそうです。
いよいよディープラーニング
さて、それでは図のようにもう一層追加してみましょう。
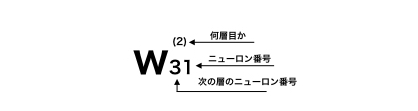
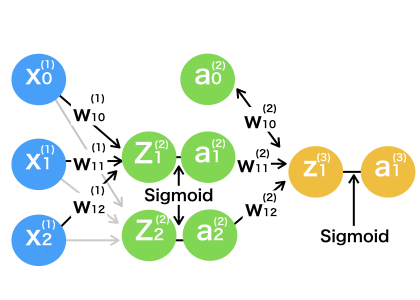
文字につく係数が少しややこしいですが、慣れれば単純です。先ほど同様に肩につくかっこは層の番号、右下の文字の左側は次の層で結合するニューロンの番号、右側は現在の層で結合するニューロンの番号です。見やすいように2層目2番目のニューロン結合の重みは省略しています。
まず、初めの入力は1サンプルで1行2列の行列です。(図ではx1とx2は縦にならんでいますが、実際に計算させる場合は横並びになります。)その入力に2行2列の1層目重み行列をかけ、バイアスを足します。すると1行2列の新たなニューロンが出来上がるので、シグモイド関数で活性化させます。

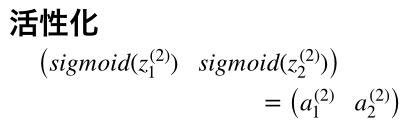
この2層目のにそれに2行1列の2層目重み行列をかけると1行1列、つまり1つの値になり、最後にもう一度活性化して、出力とします。。
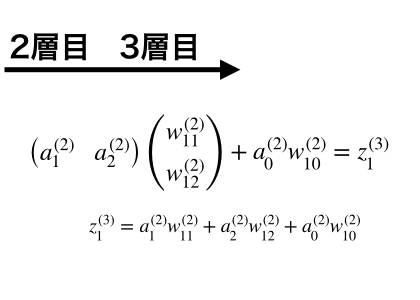
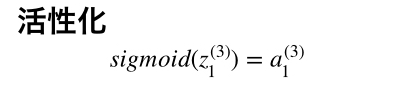
このがクラスに属する確率となります。このように層を増やすと何が良いかというと、ロジスティック回帰モデルでは表すことのできなかった非線形のクラス分類を行うことができます。
Pythonによる実装
さて、これで準備が整いました。上述のロジスティック回帰モデルが作れれば、なんてことはありません。実際にpythonでディープラーニング を実装していきましょう。
#フォワードプロパゲーションの実装 def forward(W_1,W0_1,W_2,W0_2,X): #1層目 z_2 = np.dot(X,W_1)+W0_1 #(1×2)(2×2) = (1×2) a_2 = sigmoid(z_2) #2層目 z_3 = np.dot(a_2,W_2)+W0_2#(1×2)(2×1) = (1×1) #活性化 a_3 = sigmoid(z_3) return a_3 #重みの設定 W0_1 = np.array([-0.97, 1.35]) W_1 = np.array([[0.32,-3.5],[2.34,0.41]]) W0_2 = -1.1495501 W_2 = np.array([-5.17,4.1])
先ほど同様に決定境界と正解率を出してみましょう。
#決定境界の可視化 x1_min, x1_max = X[:, 0].min()-1, X[:, 0].max()+1 x2_min, x2_max = X[:, 1].min()-1, X[:, 1].max()+1 x1_mesh, x2_mesh = np.meshgrid(np.arange(x1_min, x1_max, 0.05), np.arange(x2_min, x2_max, 0.05)) X_mesh = np.array([x1_mesh.ravel(), x2_mesh.ravel()]).T y_mesh = np.array(list(map(predict, forward(W_1,W0_1,W_2,W0_2,X_mesh)))) y_mesh = y_mesh.reshape(x1_mesh.shape) plt.contourf(x1_mesh, x2_mesh, y_mesh, alpha=0.4,cmap="Greens") plt.xlim(x1_mesh.min(), x1_mesh.max()) plt.ylim(x2_mesh.min(), x2_mesh.max()) plt.scatter(x1_0,x2_0,color="y",label="0") plt.scatter(x1_1,x2_1,color="green",label="1") plt.xlabel("x1",size=15) plt.ylabel("x2",size=15) plt.tick_params(labelsize=18) plt.legend(loc='upper left',fontsize=15) plt.show() #正解率 pred =list(map(predict, forward(W_1,W0_1,W_2,W0_2,X))) print("accuracy {:.2f}".format(sum(pred==y)/len(y))) >>accuracy 0.91
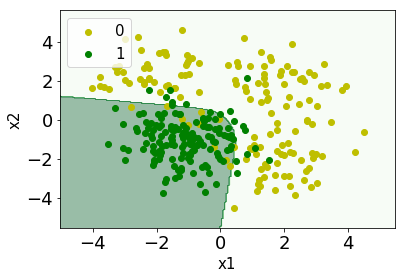
なんと、決定境界がグニャッと曲がって上手く識別できるようにっています!正解率も大幅に改善し、91%となりました。このようにディープラーニング では層を増やしていくことで、より複雑なクラス分類ができるようになります。
補足:文字の記述について
ここで、文字の記述について、参考にする本やサイトで多少異なるため、少し補足しておきます。まず、層の数え方ですが、本記事では入力を1層目とし、出力を3層目としましたが、入力、出力を除き、中間の層から数える場合もあります。また、活性化する前の線型結合をzと活性化後をaと表しましたが、上記の参考書では、逆になっています。私はアクティベーション後がaである方が分かりやすいので、そうしてありますが、理解しやすい覚え方で進めていきましょう。
まとめ
今回は親しみやすいロジスティック回帰モデルから、ディープラーニング の一連の流れを書いてみました。ディープラーニング は非線形な関係を表すことができるとても強力な機械学習モデルです。次回は、ディープラーニング の醍醐味である勝手に重みを学習するバックプロバゲーションについても書いてみます。
※本記事は筆者が個人的に学んだことをまとめた記事なります。所属する組織の意見・見解とは無関係です。また、数学の記法や詳細な理論、用語等で誤りがあった際はご指摘頂けると幸いです。
参考
誰もが知っているこちらの書籍。ディープラーニング を学ぶなら、一度は目にしておきたい一冊です。

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
- 作者:斎藤 康毅
- 発売日: 2016/09/24
- メディア: 単行本(ソフトカバー)
Rコード
データ生成アルゴリムの違いからか、正解率が本文と異なりますが、流れは一緒なのでご容赦を
library(tidyverse) #データの作成 x1_0 <- c(rnorm(n=50,2,1),rnorm(n=50,-2,1),rnorm(n=50,2,1)) x2_0 <- c(rnorm(n=50,-2,1),rnorm(n=50,2,1),rnorm(n=50,2,1)) x1_1 <- rnorm(n=150,-1,1) x2_1 <- rnorm(n=150,-1,1) X <- matrix(c(x1_0,x1_1,x2_0,x2_1),ncol=2) y <- rep(c(0,1),c(150,150)) #データシャッフル p=sample(seq(1:300),300,replace = F) X = X[p,] y = y[p] #可視化 plot(x1_0,x2_0,col="orange",xlab="x1",ylab="x2") points(x1_1,x2_1,col="green") legend(x="topleft",legend = c(0,1),pch = 1,col=c("orange","green")) #ディープラーニング風ロジスティック回帰 #シグモイド関数 sigmoid <- function(x){ return(1/(1+exp(-x))) } #フォワードプロバゲーション関数 forward <- function(W_1,W0_1,X){ #1層目 z_1 = X %*% W_1+W0_1 #活性化 a_1 = sigmoid(z_1) return(a_1) } #重み W_1 = c(-0.95,-0.88) W0_1 = -0.56 #予測関数 predict <- function(x){ if(x>=0.5){ return(1) }else{ return(0) } } #決定境界の可視化 px <- seq(min(X[,1])-1,max(X[,1])+1,by=0.05) py <- seq(min(X[,2])-1,max(X[,2])+1,by=0.05) X_mesh <- as.matrix(expand.grid(px,py)) y_mesh <- map_dbl(forward(W_1,W0_1,X_mesh),predict) plot(x1_0,x2_0,col="orange",xlab="x1",ylab="x2") points(x1_1,x2_1,col="green") contour(px,py,array(y_mesh,dim=c(length(px),length(py))) ,xlim=c(min(X[,1])-1,max(X[,1])+1), ylim=c(min(X[,2])-1,max(X[,2])+1),col="green",lwd=1, drawlabels=F, add=T) legend(x="topleft",legend = c(0,1),pch = 1,col=c("orange","green")) #正解率 pred =map_dbl(forward(W_1,W0_1,X),predict) print(str_c("accuracy ",sum(pred==y)/length(y))) #ディープラーニングフォワードプロバゲーション関数 forward<- function(W_1,W0_1,W_2,W0_2,X){ #1層目 z_2 <- (X %*% W_1)+W0_1 #(1×2)(2×2) = (1×2) a_2 <- sigmoid(z_2) #2層目 z_3 <- (a_2 %*% W_2)+W0_2#(1×2)(2×1) = (1×1) #活性化 a_3 <- sigmoid(z_3) return(a_3) } #重みの定義 W0_1 <- c(-0.97, 1.35) W_1 <- matrix(c(0.32,-3.5,2.34,0.41),ncol=2,byrow = T) W0_2 <- -1.1495501 W_2 <- c(-5.17,4.1) #決定境界の可視化 x <- seq(min(X[,1])-1,max(X[,1])+1,by=0.1) py <- seq(min(X[,2])-1,max(X[,2])+1,by=0.1) X_mesh <- as.matrix(expand.grid(px,py)) y_mesh <- map_dbl(forward(W_1,W0_1,W_2,W0_2,X_mesh),predict) plot(x1_0,x2_0,col="orange",xlab="x1",ylab="x2") points(x1_1,x2_1,col="green") contour(levels = 0.5,px,py,array(y_mesh,dim=c(length(px),length(py))) ,xlim=c(min(X[,1])-1,max(X[,1])+1), ylim=c(min(X[,2])-1,max(X[,2])+1),col="green", drawlabels=F, add=T) legend(x="topleft",legend = c(0,1),pch = 1,col=c("orange","green")) #正解率 pred =map_dbl(forward(W_1,W0_1,W_2,W0_2,X),predict) print(str_c("accuracy ",sum(pred==y)/length(y)))