初歩からの機械学習:ロジスティック回帰~PythonとRでスクラッチから~

前回は機械学習において最も基本的なアルゴリズムである最急降下法を使って、重回帰モデルを作成しました。

www.medi-08-data-06.work

今回は、最急降下法とロジスティック回帰モデルを使って機械学習の醍醐味である分類問題を扱っていきたいを思います。

前回同様PythonとRでスクラッチ からコードを書いてありますので、参考にしてみてください。

ロジスティック回帰モデルの損失関数

最急降下法では、損失関数を最小にする値を微分によって少しずづ求めていくアルゴリズムでした。重回帰モデルでは、以下の損失関数を最小にしましたね。

今回のロジスティック回帰では、予測したいアウトカム(y)は二値、つまり0or1となります。アウトカムが二値なので、上記のような損失関数は使えません。 そこで、ロジスティック回帰では二項分布の対数尤度を最大化するようにパラメーターを求めていきます。

www.medi-08-data-06.work

式で表すと、

となります。関数hは、シグモイド関数（ロジスティック関数）つまり、クラスが1となる確率が帰ってきます。対数尤度の最大化なので、マイナスをつけると最小化におきかわるので、これをコスト関数と定義します。そしてこのコスト関数をそれぞれのパラメーターで偏微分すると、

で偏微分

で偏微分

となります。偏微分の導出はこちらがわかりやすいです。

第19回 ロジスティック回帰の学習：機械学習 はじめよう｜gihyo.jp … 技術評論社

あとはこれをベクトルに書き直し、最急降下法の式に入れて

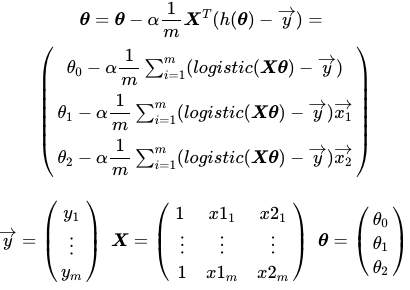
として、パラメーターを求めていきます。これは前回もやりましたね。

今回のお題

今回も前回扱ったボストンデータセットを使いますが、ボストンデータセットは 家賃が連続量であるため、家賃の中央値より高いか低いかの二値に変換して、どちらのクラスに分類されるかを予測してみます。予測に使う変数は前回同様、部屋の広さと低所得者の割合です。まずは、Xとｙを定義してグラフにしてみましょう。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from sklearn.datasets import load_boston
from sklearn import linear_model
% matplotlib inline

boston = load_boston()
data = pd.DataFrame(boston.data,columns=boston.feature_names)

X = data[["RM",'LSTAT']]
X = sm.add_constant(X) #最初の列に1を加える
#家賃の中央値より高かったらクラス1、そうでなかったらクラス0
y = np.array(list(map(lambda x :1 if x > np.median(boston.target) else 0,boston.target)))

#可視化
plt.scatter(data.RM[y==1],data.LSTAT[y==1],color="r")
plt.scatter(data.RM[y==0],data.LSTAT[y==0],color="b")
plt.xlabel("Room")
plt.ylabel("LSTAT")
plt.show()

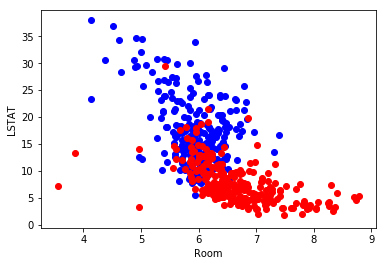
どうやら部屋の広さが大きくなるほど、低所得者の割合が小さくなるほどクラス1に分類される物件が多そうですね。これをロジスティック回帰モデルでクラス分類してみます。シグモイド関数と、コストの格納・パラメーター更新を行う関数を定義しておきます。

def h(X,theta) :
    return 1/(1+np.exp(-(np.dot(X,theta))))

def grad_desc(theta,alpha,itera,X,y):
    m = len(y)
    cost = np.zeros(itera)
    
    for i in range(itera):
        cost[i] = -1*(1/m)*np.sum(y*np.log(h(X,theta))+(1-y)*np.log(1-h(X,theta)))
        theta = theta - alpha*(1/m)*np.dot(X.T,(h(X,theta)-y))
    return [cost,theta]

前回とほとんど同じですが、ロジスティック回帰モデルの式に合わせてコスト関数とパラメーター変換の式を変えてあります。grad_descでは、更新されたパラメーターのベクトルが返ることに注意しましょう。

これで準備が整いました。実際にパラメーターをもとめてみます。

alpha = 0.01
itera = 1000
#thetaの初期値は正規分布から乱数を発生
np.random.seed(seed=123)
init_theta = np.random.randn(X.shape[1])
cost , theta = grad_desc(init_theta,alpha,itera,X,y)

#thetaの確認
print(theta)
>>[-1.12295986  0.86537999 -0.36485182]

#コストの可視化
plt.plot(cost)
plt.xlabel("Cost")
plt.ylabel("Iteration")
plt.show()

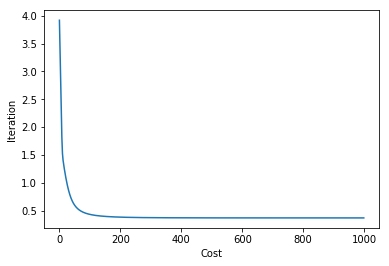
イテレーションが増えるほどコストが減っているようなので、うまくいっているようです。試しにsklearnを使ってロジスティック回帰を行った結果と比較してみましょう。

logistic = linear_model.LogisticRegression()
logistic.fit(X.iloc[:,[1,2]],y)

print(logistic.intercept_)
print(logistic.coef_)
>>[-0.66823182]
>>[[ 0.79734104 -0.3676968 ]]

若干違いますが、大体あっているようです。大きく異なっているようだと最急降下法がうまく収束していない可能性があります。

さて、ここからいよいよクラス分類をしていきます。先ほど求めたパラメーターとシグモイド関数を使って、クラスが1となる確率が0.5を超えた場合にクラス1と予測をします。

pred = np.array(list(map(lambda x : 1 if x >= 0.5 else 0, h(X,theta)))) 

この予測値から正解率（accuracy）をと求めてみると

print("accuracy {:.2f}".format(sum(pred==y)/len(y)))
>>accuracy 0.83

約84%の正解率みたいですね！ただし、今回はトレーニングデータのみの正解率で、新たなデータに対するモデル性能評価はしていないことに注意しましょう。

ついでに先ほどのグラフに決定境界を書いてみます。決定境界の書き方はこちらを参考にしました。

[第2版]Python 機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)

x1_min, x1_max = X.iloc[:, 1].min()-1, X.iloc[:, 1].max()+1
x2_min, x2_max = X.iloc[:, 2].min()-1, X.iloc[:, 2].max()+1
x1_mesh, x2_mesh = np.meshgrid(np.arange(x1_min, x1_max, 0.01),
                                   np.arange(x2_min, x2_max, 0.01))
X_mesh = sm.add_constant(np.array([x1_mesh.ravel(), x2_mesh.ravel()]).T)
y_mesh = np.array(list(map(lambda x : 1 if x >= 0.5 else 0, h(X_mesh,theta)))) 
y_mesh = y_mesh.reshape(x1_mesh.shape)

plt.contourf(x1_mesh, x2_mesh, y_mesh, alpha=0.4,cmap="Greens")
plt.xlim(x1_mesh.min(), x1_mesh.max())
plt.ylim(x2_mesh.min(), x2_mesh.max())
plt.scatter(data.RM[y==1],data.LSTAT[y==1],color="r")
plt.scatter(data.RM[y==0],data.LSTAT[y==0],color="b")
plt.xlabel("Room")
plt.ylabel("LSTAT")
plt.show()

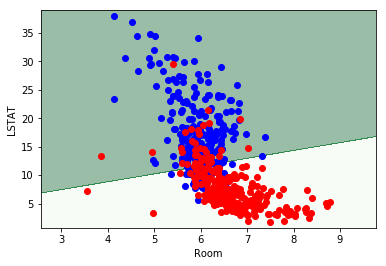
うまく分類できているようです！ちなみに、ロジスティック回帰モデルは見ての通り線形にしか分離ができません。

まとめ

ロジスティック回帰モデル単体で使う機会は少ないですが、ニューラルネットなどのモデルを作る際の基礎的な部分が共通しています。応用的な機械学習モデルを作る際には、是非ともマスターしておきたいところです。

※本記事は筆者が個人的に学んだことをまとめた記事なります。所属する組織の意見・見解とは無関係です。また、数学の記法や詳細な理論、用語等で誤りがあった際はご指摘頂けると幸いです。

参考

pythonで機械学習を始めるにはまずはこの書籍から始めるのが良いかもしれません。多くの機械学習モデルを網羅していて、これ一冊をマスターするだけでも、最低限実務で使えるレベルまでになるかと思います。

[第2版]Python 機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)

Machine Learning | Coursera

www.medi-08-data-06.work

Rコード

library(tidyverse)

X <- matrix(c(rep(1,nrow(Boston)),Boston$rm,Boston$lstat),ncol=3)
y <- if_else(Boston$medv > median(Boston$medv),1,0)

#可視化
plot(X[y==1,2],X[y==1,3],col="red",xlab="Room",ylab="LSTAT",
     xlim = c(min(Boston$rm),max(Boston$rm)),
     ylim = c(min(Boston$lstat),max(Boston$lstat)))
points(X[y==0,2],X[y==0,3],col="blue")

#ロジスティック関数
h <- function(X,theta){
  return(1/(1+exp(-(X %*% theta))))
}

#コストの格納とパラメーター更新の関数
grad_desc <- function(theta,alpha,itera,X,y){
  m <- length(y)
  cost <- numeric(itera)
  
  for(i in 1:itera){
    cost[i] <-  -1*(1/m)*sum(y*log(h(X,theta))+(1-y)*log(1-h(X,theta)))
    theta <-  theta - alpha*(1/m)*(t(X) %*% (h(X,theta)-y))
  }
  return(list(cost,theta))
}


#最急降下法の実行
alpha <-  0.01
itera <-  1000
set.seed(123)
init_theta <-  rnorm(dim(X)[2])
res <-  grad_desc(init_theta,alpha,itera,X,y)
cost <- res[[1]]
theta <- res[[2]]

print(theta)
plot(cost,xlab="Cost",ylab="Iteration")

#通常のロジスティック回帰
glm(y~X[,2]+X[,3],family = binomial())


#予測
pred <- if_else(h(X,theta)>=0.5,1,0)
print(str_c("accuray ",sum(y==pred)/length(y)))


#決定境界の可視化
px <- seq(min(X[,2])-1,max(X[,2])+1,by=0.01)
py <- seq(min(X[,3])-1,max(X[,3])+1,by=0.01)
X_mesh <- expand.grid(px,py)
X_mesh$Var0 <- 1
X_mesh <- as.matrix(X_mesh[,c(3,1,2)])
y_mesh <- if_else(h(X_mesh,theta)>=0.5,1,0)

plot(X[y==1,2],X[y==1,3],col="red",xlab="Room",ylab="LSTAT",
     xlim = c(min(Boston$rm),max(Boston$rm)),
     ylim = c(min(Boston$lstat),max(Boston$lstat)))
points(X[y==0,2],X[y==0,3],col="blue")
contour(px,py,array(y_mesh,dim=c(length(px),length(py)))
        ,xlim=c(min(X[,2])-1,max(X[,2])+1),
        ylim=c(min(X[,3])-1,max(X[,3])+1),col="green",lwd=3, drawlabels=F, add=T)