第2回：RとPythonで学ぶデータサイエンス数学~関数と微分・偏微分~

RとPythonで学ぶデータサイエンス数学の第2回となる今回は、関数と微分を扱っていきます。

この2つは統計学、機械学習の学習には欠かせない知識となりますが、概念自体は難しく無いので、しっかりと理解したいところです。目的は以下の通りです。

関数 $f(x)$ の意味が分かる。
微分を $\dfrac{d}{dx}f(x)=\lim_{h\to0} \dfrac{f(x+h)-f(x)}{h}$ で表すことができる。
偏微分を $\dfrac{\partial}{\partial x}f(x,y)$ , $\dfrac{\partial}{\partial y}f(x,y)$ で表すことができる。

今回も吐き気がするような数式ですが、丁寧に解説していくのでご安心ください。誰が読んでも理解できることを目指していますので、分かりにくい、理解できない等ありましたら、お気軽にコメント頂けると幸いです。なお、RやPythonを使わなくても、学ぶことができる内容ですので、数学の知識だけ学びたいという方も是非ご覧ください（^^）

関数とは？
微分とは?
微分の公式
- Rで微分
- pythonで微分
微分の使いみち
- R
- python
偏微分とは？
偏微分の実践
- Rで偏微分
- pythonで偏微分
合成関数の微分
まとめ
参考

なお、本記事は主に以下を参考にしています。

データサイエンスのための数学 (データサイエンス入門シリーズ)

作者:椎名洋,姫野哲人,保科架風
出版社/メーカー: 講談社
発売日: 2019/08/31
メディア: 単行本

統計学が最強の学問である[数学編]――データ分析と機械学習のための新しい教科書

作者:西内啓
出版社/メーカー: ダイヤモンド社
発売日: 2017/12/21
メディア: 単行本（ソフトカバー）

関数とは？

関数を理解することは、統計、機械学習の理論を学ぶためだけでなく、実際の解析を行うためのコードを書く際にも必要です。関数とは、簡単に言ってしまうと電卓です。例えば、入力した値を2で割るだけ電卓があったとしましょう。入力する値をxとして、電卓を" $電卓(x)$ "と表すことにします。この電卓の中身は、入力された値xを2で割るだけなので、

$電卓(x) = \dfrac{x}{2}$

と表すことができます。この時、10を入力すると5が出力されるので、

$電卓(10)= \dfrac{10}{2} = 5$

となります。

データサイエンス数学

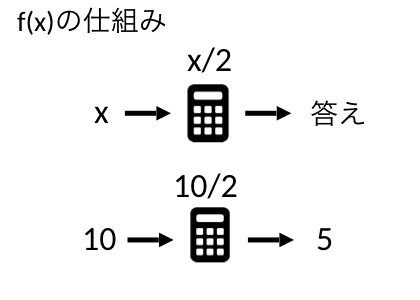
Rではfuncition、pythonではdefを使って関数を作成します。

#関数を作る
dentaku <- function(x){
  return(x/2)
}

#値を入力
print(dentaku(10))
>5

#関数を作る
def dentaku(x):
    return x/2 

#値を入力
print(dentaku(10))
>5

このように関数とはある値を入力すると、何らかの計算を行って、答えを出力してくれるものです。電卓の中身が変わることで、様々な関数を作ることができます。このまま" $電卓(x)$ "ではかっこ悪いので、functionのfをとって $f(x)$ と表すことにします。

また、関数への入力は2つ以上でもよくて、例えば、入力された値を足し合わせるという関数を作ることもできます。入力する2つの値を $x_{1}=5, x_{2}=10$ とすると

$f(x_{1}, x_{2} ) = x_{1}+x_{2}\\ f(5,10) = 5+10 = 15$

となります。

データサイエンス数学

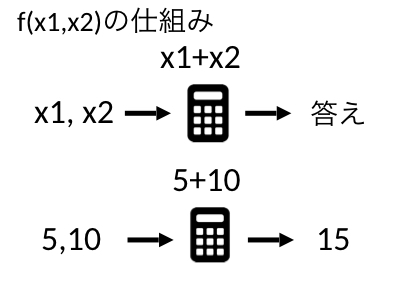
#2つの値を入力できる関数
fx1x2 <- function(x1,x2){
  return(x1+x2)
}

print(fx1x2(5,10))
>15

#2つの値を入力できる関数
def fx1x2(x1,x2):
    return x1+x2

print(fx1x2(5,10))
>15

中学、高校でf(x)とyは同じものだと教わった方もいるかもしれませんが、出力の結果をyと表した場合にy=f(x)となり、厳密には、f(x)は電卓（関数）、yは答えであることには注意しましょう。

微分とは?

関数を理解したところで、お次は微分に入ります。微分とは傾きを求めるための手法です。微分によって傾きを求めることは、統計や機械学習の様々なところで役に立ちます。まずは、こんな関数を考えてみましょう。

$f(x) = (x-10)^{2}$

fx <- function(x){
  return((x-10)^2)
}

def fx (x):
    return (x-10)**2

これをみて驚いた方は、入力した値から10を引いて2乗した結果を出力する電卓、と置き換えてください。この関数に入力する値xを変化させて、グラフにしたものがこちらです。

データサイエンス数学

ここで、まずは(10,0)と(20,100)を通る赤色の直線の傾きを求めてみます。傾きは小学校、中学校で習った

$傾き = \dfrac{yの増加量}{xの増加量}$

で求めることができます。そして、この増加量のことを数学では、Δ（デルタ）または、d（diference）で表すことが多く、以下のように書き換えられます。

$傾き = \dfrac{dy}{dx}$

今後はdを使った書き方をしていくので、ここで、しっかりと意味を理解しておきましょう。さて、傾きですが、xの増加量は10から20に増えているので、 $dx=10$ です。続いてyの増加量ですが、これは関数を使って表してみます。

$dy =f(20) - f(10) \\ = (20-10)^{2}-(10-10)^{2}\\ =100$

となります。ですので赤線の傾きは

$傾き = \dfrac{dy}{dx}\\ = \dfrac{f(20) - f(10)}{10} \\=100/10 \\=10$

です。

dx <- 10
dy <- fx(20)-fx(10)
print(dy)
>100
print(dy/dx)
>10

dx = 10
dy = fx(20)-fx(10)
print(dy)
>100
print(dy/dx)
>10

ここで、xの増加量である10をhと置き換えてみると、上の式はこのように書き換えることができます。

$傾き = \dfrac{f(20) - f(10)}{10} \\=\dfrac{f(10+h) - f(10)}{h}$

それでは次にこのhの幅を少しずつ短くした時の傾きをみてみましょう。

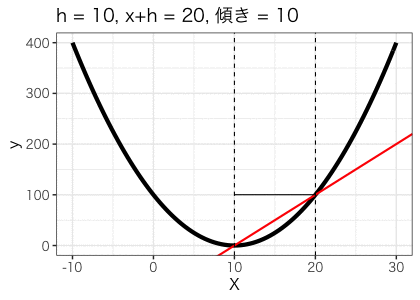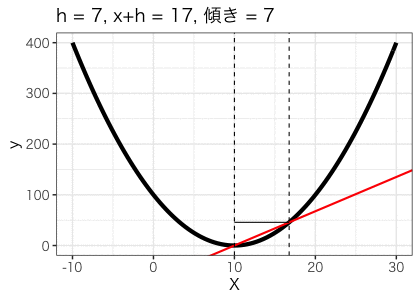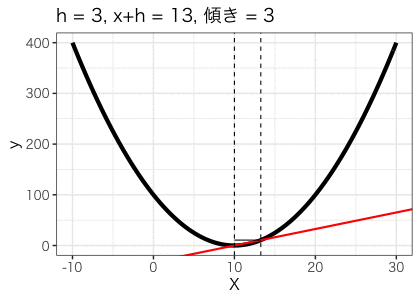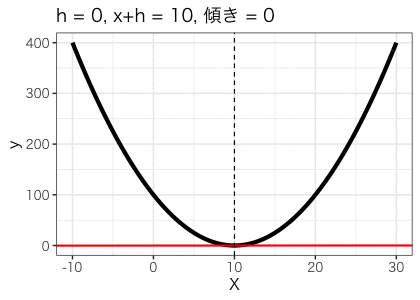
hが短くなるにつれて傾きが小さくなり、最終的に0になりました。これはx=10のときの傾きが0であることを表しています。

今度は、

$傾き=\dfrac{f(20+h) - f(20)}{h}$

とした際に、hを徐々に短くしてみましょう。

最終的に傾きは、20となり、x=20の点での傾きを表しています。傾きを求めるためには2つの点が必要ですが、その2点間の距離を0に近づけていくことで、関数上の任意の点での傾きを近似的に求めることできます。つまり、接線みたいなものです。これが微分です！

このhを限りなくゼロに近づけていくことを数学では、極限といい英単語Limitを使って

$\lim_{h\to0}$

と表現します。さらに先ほどの式と組み合わせると、関数f(x)上のある点xでの傾きは、

$傾き=f(x)'= \lim_{h\to0} \dfrac{f(x+h) - f(x)}{h}$

となります。この $f(x)'$ は、関数f(x)上の点xでの傾きという意味で、導関数とも呼ばれます。例えば、x=10の傾きは0でした。上記に値を入れて確認してみます。

$f(10)'= \lim_{h\to0} \dfrac{f(10+h) - f(10)}{h} \\= \lim_{h\to0} \dfrac{(10+h-10)^{2} - (10-10)^{2}}{h} \\= \lim_{h\to0} \dfrac{h^{2} - 0}{h} \\= \lim_{h\to0} h$

ここがポイントですが、極限では、hが最終的に0になるのでh=0とします。すると答えは0になり、これがx=10の点での傾きとなります。また、x=20としてみると

$f(20)= \lim_{h\to0} \dfrac{f(20+h) - f(20)}{h} \\= \lim_{h\to0} \dfrac{(20+h-10)^{2} - (20-10)^{2}}{h} \\= \lim_{h\to0} \dfrac{h^{2}+20h +100-100}{h} \\= \lim_{h\to0} h+20$

となるので、hを0にすると20となることが分かります。

RやPythonでは、h=0にすると計算ができないため、hには1のマイナス10乗などとても小さい値にします。

#eは指数表記を表し、e-1 = 0.1
#hは1のマイナス10乗に設定する
h <-  1e-10

#x=10のとき
x <-  10
print((fx(x+h)-fx(x))/h)
>1e-10 #1のマイナス10乗なので、ほとんど0

#x=20のとき
x <- 20
(fx(x+h)-fx(x))/h
>19.99965 #ほとんど20

#eは指数表記を表し、e-1 = 0.1
#hは1のマイナス10乗に設定する
h =  1e-10

#x=10のとき
x =  10
print((fx(x+h)-fx(x))/h)
>1.0000001654807488e-100 #1のマイナス10乗なので、ほとんど0

#x=20のとき
x = 20
print((fx(x+h)-fx(x))/h)
>19.99964638343954 #ほとんど20

微分の公式

ここまでで、微分を

$\dfrac{dy}{dx}=f(x)'= \lim_{h\to0} \dfrac{f(x+h) - f(x)}{h}$

で表わすことができるようになりました。しかし、いちいち傾きを求めるために、上記の式に代入して、h=0とするのは大変です。そこで、微分には便利な公式がたくさんあります。後々に様々な公式を紹介するとして、今の段階では、1つだけ紹介します。

$f(x) = x^{n}$

$\dfrac{d}{dx}f(x)=f(x)'=nx^{n-1}$

上の左辺は、出力結果をyで表すとは限らないので、dyのyをf(x)に置き換えたこちらの書き方が一般的です。右辺は入力の値xをn乗する関数を微分すると $nx^{n-1}$ となることを表しています。実際に先ほどの関数を使ってやってみましょう。

$f(x) = (x-10)^{2} = x^{2}-20x+100$

$\dfrac{d}{dx}f(x) = 2x^{1}-20x^{0} \\= 2x-20$

$f(10)' = 0\\ f(20)' = 20$

と同じになりましたね！ポイントは、xに関係のない項は無視できるところです。この微分を理解するだけで、統計、機械学習の学びが大きく前進します！RやPythonで微分を行う方法は、少し複雑になるので、下記に分けて書いていきます。

Rで微分

Rで微分を行うには、最初にexpressionで関数(fx)を定義し、driveを使うと、expressionで定義された関数の導関数(fd)が算出されます。導関数に値を入れると、元の関数に入れた時の値（fxの出力値）と、導関数に入れた時の値（傾き）が算出されます。

#expressionで関数を定義
fx <- expression((x-10)^2)

#derivで関数を微分
fdx <- deriv(fx, "x", func=T)

#微分後の導関数 
print(D(fx,"x"))
>2 * (x - 10)
 
# x=10で微分
print(fdx(10))
>[1] 0
>attr(,"gradient")
>     x
>[1,] 0

# x=20で微分
print(fdx(20))
>[1] 100
>attr(,"gradient")
>      x
>[1,] 20

pythonで微分

pythonで微分を行うには、代数計算ライブラリsympyを使います。sympyは、計算結果をTex形式で出力してくれるとても便利なライブラリです。初めての方はインストールしておきましょう。

Python, SymPyの使い方（因数分解、方程式、微分積分など） | note.nkmk.me

conda install sympy
#or
pip install sympy

最初にsym.symbolsで使いたい文字を定義し、関数(fx)を作ります。sym.diffを使うと、定義された関数の導関数(fdx)が算出されます。導関数を代入すた変数で、subsを使うと微分後の傾きが算出されます。引数は導関数の中で値を代入したい文字(ここではx)と、その値を渡します。

#インポートと出力用の設定
import sympy as sym
sym.init_printing(use_unicode=True)

# 使用したい文字を定義
x= sym.symbols("x")

#関数を定義
fx = (x-10)**2

#導関数
fdx = sym.diff(fx)

#微分後の導関数 
print(fdx)
>2*x - 20

# x=10で微分
print(fdx.subs(x,10))
>0

# x=20で微分
print(fdx.subs(x,20))
>20

微分の使いみち

それでは、実際にどのように微分が使われるのか見ていきましょう。先程の関数は、x=10のところで傾きが0となりました。実はこのx=10というのは、関数の値を最小にするxの値となります。統計学、機械学習では、このよう微分した値が0になるところが、ある関数の値を最大または最小にする入力の値となる性質を頻繁に利用します。

例えば、今度はこんな関数を考えてみましょう。

$f(x) = 4x^{2} - 80x+500$

この関数を最小とするxの値を求めてみます。微分の公式を使うと

$\dfrac{d}{dx} f(x) = 8x - 80$

となります。そして、傾きが0になれば良いので、イコール0として方程式を解いてみると

$8x - 80 = 0\\ x=10$

となり、x=10が関数f(x)を最小にする値となることが分かります。そして、このときの最小値は、

$f10) = 4*100 - 800 + 500 = 100$

ですね。その他の値をxに入れて傾きと関数の値を可視化したものが以下になります。

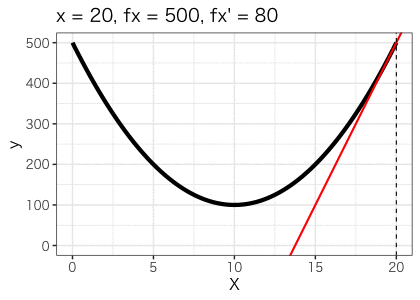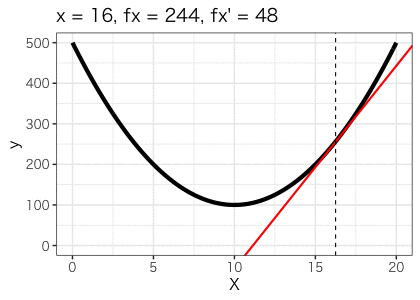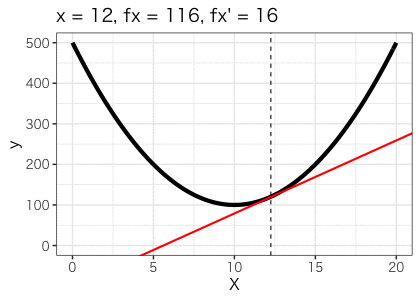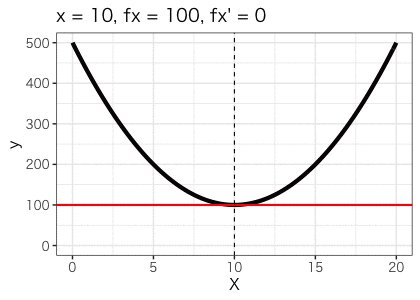
確かにx=10で、傾きが0となり、関数の値は最小値をとることが分かります！

R

Rのunirootはf(x) =0 の解を求めるための関数です。expressionで定義した関数をDを使うことで、導関数を出力し、その結果を新たに関数として定義します。それをunirootで0となる解を求めます。出力は$rootが入力の値、$f.rootは、出力値で、内部ではニュートン法を使っているため、f(x) =0となるxが存在する範囲を指定する必要があることに注意してください。

ニュートン法とは何か？？ニュートン法で解く方程式の近似解 - Qiita

#関数を定義
fx <- expression(4*x^2-80*x+500) 

#微分後の導関数を確認
print(D(fx,"x"))
>4 * (2 * x) - 80

# 導関数を関数として定義
fdx <- function(x){4 * (2 * x) - 80}

# unirootで方程式を解く
#範囲を指定する必要がある。
res <- uniroot(fdx, c(-10, 20))
print(res$root)
>[1] 10

python

pythonでは、先ほど同様にdiffで微分した後、solveを使って方程式を解きます。solveは関数=0となる値を求める関数で、答えはリスト形式で返ってきます。

fx = 4*x**2-80*x+500
fdx = sym.diff(fx)
print(sym.solve(fdx)[0])
>10

偏微分とは？

さて、最後は微分の進化系である偏微分です。偏微分は、名前の通り偏った微分で、微分する文字が2つ以上になるときに使います。例えばこんな関数を考えてみましょう。

$f(x,y)= (x-y)^{2}+(x-10)^{2}+(y-5)^{2}$

今度は、入力の値がxとyの2つです。ここでも頭の中で電卓をイメージしてみます。例えば、x=5、y=10とすると

$f(5,10) = 75$

となります。

データサイエンス数学

この関数にx,yをいろいろ変えて出力した値、3次元グラフにしてました。

このように、同じxやyの値でも、相方の値によって傾きの値が変わり、関数を最小にするx,yの値が異なるときに偏微分を使います！

偏微分といっても、何か新しいことをするわけではないです。ただ、偏微分の記号には慣れておきましょう。このように書きます。

$関数をxで偏微分 : \dfrac{\partial}{\partial x} f(x, y)$

$関数をyで偏微分: \dfrac{\partial}{\partial y} f(x, y)$

偏微分の実践

それでは、実際に偏微分を実践していきましょう。やり方は簡単で、微分したい変数以外の変数は、ただの定数として扱うだけです。まずは、式を展開してみましょう。

$(x - 10)^{2} + (x - y)^{2} + (y - 5)^{2} \\ = 2 x^{2} - 2 x y - 20 x + 2 y^{2} - 10 y + 125$

そして、xで偏微分してみます。

$\dfrac{\partial}{\partial x} (2 x^{2} - 2 x y - 20 x + 2 y^{2} - 10 y + 125) \\= 4x-2y-20$

続いて、yでも偏微分します。

$\dfrac{\partial}{\partial y} (2 x^{2} - 2 x y - 20 x + 2 y^{2} - 10 y + 125) \\= -2x+4y-10$

データサイエンス数学

このように、偏微分をしたい変数に関係のない部分は、あたかも定数のように扱うことができます。最後にどちらの式でも傾きが0になればよいので、イコール0とすると

$\left\{ \begin{array}{l} 4x - 2y -20 = 0 \\ -2x + 4y - 10 = 0 \end{array} \right.$

中学校でならう連立方程式の問題となります。これを解いてみると

$x=\dfrac{25}{3}, y=\dfrac{20}{3}$

が答えとなって、これがこの関数を最小にするxyの値となります。

Rで偏微分

Rで偏微分を行うには、少し工夫が必要で、連立方程式を行列の形で書く必要があります。そのため、

$\left\{ \begin{array}{l} 4x - 2y = 20 \\ -2x + 4y = 10 \end{array} \right.$

と、左辺を文字だけ、右辺を数字だけの連立方程式に直します。それをsolveに、右辺の行列と左辺のベクトルを渡して、逆行列なるものを求めることで解くことができます。この行列やベクトルの考え方は、後の記事でご紹介します。

fxy <- expression((x-y)^2+(x-10)^2+(y-5)^2) 

#xで偏微分した導関数を確認
print(D(fxy,"x"))
>2 * (x - y) + 2 * (x - 10)

#yで偏微分した導関数を確認
print(D(fxy,"y"))
>2 * (y - 5) - 2 * (x - y)

#連立方程式
#左辺を行列型に直す。
sahen <- matrix(c(4,-2,-2,4),2,2)

#右辺をベクトル型に直す。
uhen <- matrix(c(20,10),2,1)
print(sahen)

   [,1] [,2]
[1,]    4   -2
[2,]   -2    4

print(uhen)
   [,1]
[1,]   20
[2,]   10

#関数を最小にする答え
solve(sahen,uhen)
>        [,1]
[1,] 8.333333
[2,] 6.666667

また、関数を最小にする値を求めるだけであれば、optimやoptimiseという関数を使うこともできるので、気になる方はこちらをご覧ください。

www.medi-08-data-06.work

pythonで偏微分

pythonでは、比較的簡単に偏微分を行うことができます。diffを使ってxとyでそれぞれ偏微分した値を、solve ni 渡して連立方程式を解きます。

x ,y  = sym.symbols("x y")
fxy = (x-y)**2+(x-10)**2+(y-5)**2

#xで偏微分した導関数
fdx = sym.diff(fxy,x)
print(fdx)
>4*x - 2*y - 20

#yで偏微分した導関数
fdy = sym.diff(fxy,y)
print(fdy)
>-2*x + 4*y - 10

#連立方程式を解く
print(sym.solve([fdx,fdy]))
>{x: 25/3, y: 20/3}

合成関数の微分

上記の関数fxyを偏微分する際に愚直に式を展開して微分を行いましたが、微分の公式には合成関数の微分という便利な公式があります。こんなやつです。

$\dfrac{df}{dx}=\dfrac{df}{du}\dfrac{du}{dx} \\= f(g(x))' g(x)'$

何のこっちゃですね。まず、１行目ですが、関数fをxで微分した値と、関数fをuで微分したものに、uをxで微分したものをかけた値は同じになることを表しています。例えば、 $f(x) = (x-10)^{2}$ を微分する際に、先ほどは展開して微分しましたが、 $u=(x-10)$ としてみると、 $f(u) = u^{2}$ となります。これをuで微分すると、