じっくり学ぶ時系列解析~多変量時系列解析VAR編~ - 医療職からデータサイエンティストへ

一変量時系列の代表格であるARIMAモデルは、過去の自分が現在へ影響していることを前提としていました。しかし、時系列データではその他の変数から影響を受けることは往々にしてあります。

例えば、あるお店の売り上げは、そのお店の過去の売り上げだけでなく、周辺のライバル店の売り上げ、景気の影響、気温、店長さんの気分など様々な要因が影響すると考えらます。

そんな多数の変数同士の関連も含めて考えることができるのが、多変量時系列モデルの良いところです。

さらには、ライバル店の売り上げは、自分のお店の売り上げにはどれぐらい影響があるのか、など変数間の動的な変動を見ることで因果関係も推定できてしまいます。

今回は、そんな多変量時系列解析の中でも、VARモデル、グレンジャー因果性、インパルス応答関数についてまとめていきます。

前回までの内容はこちらです。

時系列って何？ www.medi-08-data-06.work

時系列モデルってどうやって作るの？ www.medi-08-data-06.work

時系列モデルの予測ってどうやるの？ www.medi-08-data-06.work

VARモデルの概略
- 補足：VARモデルをちょっと詳しく
グレンジャー因果性
- 補足：グレンジャーの因果性をどう検定するか
インパルス応答関数
- 補足：インパルス応答関数はどうやって求めるのか？
Rでの実践
まとめ
参考書籍
その他

VARモデルの概略

多変量時系列モデルの代表的なものにARモデルを拡張したベクトル自己回帰モデル：VARモデルがあります。なぜベクトルかというと、ARモデルの係数や系列をベクトルや行列で表すことができ、多変量に拡張できるからです。詳しくはこちらを

経済・ファイナンスデータの計量時系列分析 (統計ライブラリー)

作者: 沖本竜義
出版社/メーカー: 朝倉書店
発売日: 2010/02/01
メディア: 単行本
購入: 4人クリック: 101回
この商品を含むブログ (6件) を見る

まずは簡単な一次、二変量のVARモデルを考えてみましょう。 VARモデルでは、お互いに影響し合うことを前提としているので、こんな感じになります。

$y_{t} = \phi_{y1}y_{t-1} + \phi_{x1}x_{t-1}+\epsilon_{yt}$

$x_{t} = \theta_{x1}x_{t-1} + \theta_{y1}y_{t-1}+\epsilon_{xt}$

例えば、これをライバル店同士であるY店、X店の売り上げモデルだと仮定しましょう。これが意味するところは、Y店の売り上げは、過去一期前のY店の売り上げだけでなく、X店の売り上げも関係していることを表しています。

この二店舗データを仮想的に2021年から2030年まで1ヶ月ごとに売り上げが記録されているものとして

$y_{t} = 60+0.3y_{t-1} -0.6x_{t-1}+\epsilon_{yt}$

$x_{t} = 40+0.5x_{t-1} -0.3y_{t-1}+\epsilon_{xt}$

というVARモデルで表されるデータを作成し、グラフにしたものがこちらです。

時系列

VARモデルは一見すると無相関に見えます。このようなモデルを見かけ上無相関な回帰モデル：SURモデル(seemingly unrelated regression model)と呼び、VARモデルはSURモデルの一種であると言えます。

補足：VARモデルをちょっと詳しく

VARモデルには変数同士の同時点の係数が含まれいてません。そのため、VARモデルの係数推定は、各個別の方程式に対してOLS（最小二乗法）や最尤法で係数を推定できることが知られています。この簡便さのためにVARモデルは一般的に広まったそうです。同時点の係数を含む構造VARモデル（Structural VAR model）は、係数の推定が複雑であり、様々な前提条件が必要になるためあまり用いられていません。

また、VARモデルの他にもVMAやVARMAも存在していますが、モデルの推定が困難であり、VARモデルでもかなり複雑な関係を表すことができるため、VARモデルが主に利用されているのです。

グレンジャー因果性

VARモデルを使う大きな理由の一つに、変数間に因果関係があるかどうかを調べることできるということあります。

先ほどの二店舗の売り上げデータが全く情報なく与えられたとして、この二店舗間の売り上げに因果関係があるかどうかを調べたい時に、グレンジャー因果性を使って、調べることができます。

グレンジャー因果性とは、簡単に言ってしまうと、Y店舗の売り上げに対して、Y店舗の値のみを使ったモデルと、X店舗の値を加えたモデルとで後者の方がデータに対して当てはまりがよければ、XからYに対してグレンジャー因果性があるとなります。

具体的な計算方法は省きますが、視覚的にY店舗の売り上げグラフに、 Y店舗のみのAR(1)モデルとX店舗を加えたVAR(1)モデルを重ねてみましょう。

時系列

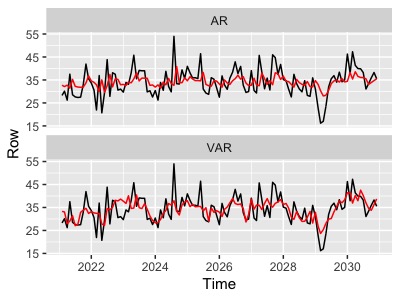
みた感じでもVARモデルの方が変動を上手く捉えて、当てはまりが良さそうですね！

実際に、グレンジャー因果性の検定なるものを行うとグレンジャー因果性ありとなります。

注意すべきはグレンジャー因果性と本物の因果性とは区別する必要があります。グレンジャー因果性はデータの関係性のみから推定されるため、本当に因果関係があるかどうかはわからないのです。

そのために因果性ではなく、グレンジャー因果性とわざわざ名前がついているのですね。

補足：グレンジャーの因果性をどう検定するか

具体的には、それぞれのモデルを作成して、残差平方和から求めた統計量を使って、f分布で検定します。まずは、Y店舗とX店舗の値を使ってVARモデルを作ります。こんなモデルでしたね。

$y_{t} = \phi_{y1}y_{t-1} + \phi_{x1}x_{t-1}+\epsilon_{yt}$

このモデルをOLSで推定し、その残差平方和をSSR1とします。

続いて、VARモデルと同じ次数のARモデル（今回はAR(1)モデル）を作成し、その残差をSSR0とします。

$y_{t} = \phi_{y1}y_{t-1} +\epsilon_{yt}$

これらの残差を使って、

$\dfrac{(SSR0-SSR1)/r}{SSR1/(T-np-1)} =\dfrac{(SSR0-SSR1)/1}{SSR1/(T-3)}$

という統計量を使って、帰無仮説をグレンジャー因果性なしとしてf検定を行います。(rはVARモデルにおけるxの項数、nは変数の数、pは次数を表す)

つまり、SSR1がSSR0に比べて十分に小さくなるときに統計量は大きくなるので、棄却されやすくなります。

インパルス応答関数

因果関係がわかれば、それがどれぐらいの大きさの影響を与え合っているのか知りたくなりますよね。そんなときに使うのがインパルス応答関数です。

インパルス応答関数は、ある変数の変動が他の変数に与える影響がどれぐらい続くかということを調べることができます。

以下をみてみましょう。

時系列

これは、店舗Xの売り上げがある一時点でプラスになったときにY店舗、X店舗の売り上げにどれぐらい影響するかを表しています。

ここからX店舗の売り上げがある一時点でプラスになるとY店舗の売り上げには、６ヶ月ぐらい続くマイナスの影響を与えていることが分かります。さらには、X店舗自身へのプラスの影響も6ヶ月ほど続いています。

次にY店舗からX店舗に与える影響をみてみましょう。

時系列

先ほどとは違い、X店舗へ少しだけマイナス影響はありますが、すぐに影響力が無くなっています。また、自店舗へのプラスの影響もすぐに無くなってしまっています。

ここからX店舗は強豪店舗で、Y店舗はX店舗から大きな影響を与えられていることが分かります。

補足：インパルス応答関数はどうやって求めるのか？

インパルス応答関数は、直感的には分かりやすいのですがその求め方は複雑です。数学的な意味としては、ある変数の誤差項（撹乱項）を１単位または１標準偏差だけ増加させた場合に、その他の変数がどれぐらい変動するかという意味になります。

インパルス応答関数には、誤差項同士の無相関を仮定した非直交化インパルス応答関数と、誤差項同士もお互いに相関することを仮定した直交化インパルス応答関数があります。

通常は直交化インパルス応答関数を使いますが、その際にはコレスキー分解を用いて、誤差項を相関する部分と無相関な部分に分割し、偏微分を使ってその変動を求めるという方法を使います。

詳しい計算方法は下記の参考書（沖本本）をご参照ください。

Rでの実践

ここからは本日の内容をRで実践していきます。まずはデータの作成です。今回はこんなVARモデルになるようにデータを作成しました。

$y_{t} = 60+0.3y_{t-1} -0.6x_{t-1}+\epsilon_{yt}$

$x_{t} = 40+0.5x_{t-1} -0.3y_{t-1}+\epsilon_{xt}$

$y_{0} = 30,x_{0} = 60,\epsilon \sim Normal(0,5)$

library(tidyverse)
library(lubridate)

set.seed(123)
year <- as.character(rep(seq(2021,2030),rep(12,10)))
month <- as.character(rep(seq(1,12),10))
day <- as.character(rep(1,120))

x <- rep(0,12*10)
y <- rep(0,12*10)
epsx <- rnorm(120,0,5)
epsy <- rnorm(120,0,5)

x[1] <- 60
y[1] <- 30

for(i in 2:120){
  y[i] <- 0.3*y[i-1]-0.6*x[i-1]+epsy[i]+60
  x[i] <- 0.5*x[i-1]-0.3*y[i-1]+epsx[i]+40
}

#データセット
sales <- data_frame(year=year,month = month,day=day,y=y,x=x) %>% 
  mutate(Times = ymd(str_c(year,month,day,sep="/"))) %>% 
  dplyr::select(Times,y,x) 

# 可視化
sales %>% 
  gather(key="shop",value="sales",-Times) %>%  
  ggplot(aes(x=Times))+
  geom_line(aes(y=sales,col=shop))

時系列

VARモデルのシミュレーションデータは{tsDyn}パッケージの、VAR.sim{tsDyn} を使っても作成できます。

#係数
B<-matrix(c(60,40,0.3,-0.3,-0.6,0.5), 2)
#初期値
S <- matrix(c(30,60),1)

#include="const"で切片(定数項)ありのモデル
sales <- VAR.sim(B=B,n=120,lag=1,include="const",starting = S)

VARモデルの推定

VARモデルを扱うためには{vars}パッケージを入れましょう。流れとしては、

VARselect{vars}を使い、AICを含む様々な情報量基準に従って次数を選択する。
推定された次数からVAR{vars}を使ってVARモデルを作成する。

です。やってみましょう。

#定数項ありのモデルで、次数を推定する
#どの情報量基準も、次数1を選んだ

> VARselect(sales[,-1],type = "const")
$selection
AIC(n)  HQ(n)  SC(n) FPE(n) 
     1      1      1      1 

$criteria
                1          2          3          4          5
AIC(n)   6.232215   6.289174   6.328314   6.321033   6.362151
HQ(n)    6.291960   6.388750   6.467719   6.500269   6.581217
SC(n)    6.379514   6.534673   6.672011   6.762930   6.902247
FPE(n) 508.895104 538.775893 560.404034 556.555104 580.269428
                6          7          8          9         10
AIC(n)   6.393768   6.417073   6.460606   6.528312   6.573285
HQ(n)    6.652664   6.715799   6.799162   6.906699   6.991502
SC(n)    7.032064   7.153568   7.295300   7.461206   7.604378
FPE(n) 599.435067 614.305546 642.649443 689.046672 722.538720


#p=1で1次のVARモデルになる。
var_mod <- VAR(sales[,-1],p=1,type = "const")
> var_mod

#Y店舗のモデル
VAR Estimation Results:
======================= 

Estimated coefficients for equation y: 
====================================== 
Call:
y = y.l1 + x.l1 + const 

      y.l1       x.l1      const 
 0.1957883 -0.5808243 62.2682011 

#X店舗のモデル
Estimated coefficients for equation x: 
====================================== 
Call:
x = y.l1 + x.l1 + const 

      y.l1       x.l1      const 
-0.1813295  0.5361587 33.8881525

どちらも生成したモデルに近い係数になってますね。

グレンジャー因果性

グレンジャー因果性はcausality{vars}で検定できます。引数のcauseでどちらからの因果性なのかを指定します。

#XからYへの因果性
> causality(var_mod,cause = "x")
$Granger

    Granger causality H0: x do not Granger-cause y

data:  VAR object var_mod
F-Test = 46.404, df1 = 1, df2 = 232, p-value = 8.19e-11


$Instant

    H0: No instantaneous causality between: x and y

data:  VAR object var_mod
Chi-squared = 2.7619, df = 1, p-value = 0.09653

#YからXへの因果性
> causality(var_mod,cause = "y")
$Granger

    Granger causality H0: y do not Granger-cause x

data:  VAR object var_mod
F-Test = 6.8309, df1 = 1, df2 = 232, p-value = 0.009545


$Instant

    H0: No instantaneous causality between: y and x

data:  VAR object var_mod
Chi-squared = 2.7619, df = 1, p-value = 0.09653

帰無仮説は因果性なしですので、どちらも有意水準1%で、因果性ありとなってますね。また$instantとあるのは、瞬時的因果性を表し、遅れてではなく、同時点での因果性があるかどうかの検定になります。こちらは、帰無仮説が棄却されず因果性があるとは言えなさそうです。

ARモデルをArima{forecast}で作成して、ARモデル、VARモデルの推定値をグラフに書いてみます。

#Y店舗のAR(1)モデルの作成
ar_mod <-Arima(sales[,2],order=c(1,0,0),include.constant = T)

#グラフ化
data_frame(Time=sales$Times[-1],
           Row = sales$y[-1],
           AR=ar_mod$fitted[,1][-1],
           VAR=var_mod$varresult$y$fitted.values) %>% 
  gather(key="model",value = values,AR,VAR) %>% 
  ggplot(aes(x=Time,col=model))+
  facet_wrap(.~ model,ncol=1)+
  geom_line(aes(y=Row),col="black")+
  geom_line(aes(y=values),col="red")

時系列

VARモデルで予測

せっかくARモデル、VARモデルを作ったので、予測を比べてみましょう。forecast{forecast}はあまり{vars}との相性がよくないので今回はpredict{stats}を使います。

#n.ageadで予測する期間を指定、今回は24ヶ月（2年）先まで予測をする
var_pred <- predict(var_mod,n.ahead = 24,ci = 0.95)
ar_pred <- predict(ar_mod,n.ahead = 24,ci = 0.95)

#予測値の可視化ARモデル
ggplot()+
  geom_line(data=sales,aes(x=Times,y=y))+
  geom_line(data=data_frame(Time = sales$Times[97:120]+years(2),
                            y=ar_pred$pred),
            aes(x=Time,y=y),
            col="blue")+
  geom_ribbon(data=data_frame(Time = sales$Times[97:120]+years(2),
                            upper=ar_pred$pred+2*ar_pred$se,
                            lower=ar_pred$pred-2*ar_pred$se),
              aes(x=Time,ymin=lower,ymax=upper),
            alpha=0.3)+
  labs(title="AR")

#予測値の可視化VARモデル
ggplot()+
  geom_line(data=sales,aes(x=Times,y=y))+
  geom_line(data=data_frame(Time = sales$Times[97:120]+years(2),
                            y=var_pred$fcst$y[,1]),aes(x=Time,y=y),
            col="red")+
  geom_ribbon(data=data_frame(Time = sales$Times[97:120]+years(2),
                            upper=var_pred$fcst$y[,2],
                            lower = var_pred$fcst$y[,3]),
              aes(x=Time,ymin=lower,ymax=upper),
            alpha=0.3)+
  labs(title="VAR")

時系列

ARモデルの場合はすぐに平均値へ回帰していますが、VARモデルは一度上方に上がり、緩やかに収束しています。

多変量時系列では、若干予測精度が上がりますが、やはり過去の変数の値しか情報を持たないために長期の予測には使いにくいです。

インパルス応答関数

最後はインパルス応答関数です。こちらはirf{tsDyn}を使います。

#n.aheadで何期先の影響まで見るのかを指定します。

imp <- irf(var_mod,n.ahead = 10)

#plot関数を使うと簡単に描画できます。
plot(imp)

#しかしいつものごとくggplotを使いました。

#Xからの影響
data_frame(impluse = as.vector(imp$irf$x),
           upper = as.vector(imp$Upper$x),
           lower = as.vector(imp$Lower$x),
           to = rep(c("y","x"),c(11,11))) %>% 
  ggplot(aes(x=rep(1:11,2),y=impluse))+
  facet_wrap(.~ to,nrow = 2)+
  geom_line(aes(color=to))+
  geom_ribbon(aes(ymax=upper,ymin=lower),alpha=0.2,linetype=2)+
  labs(title="From X",x="lag")

#Yからの影響
data_frame(impluse = as.vector(imp$irf$y),
           upper = as.vector(imp$Upper$y),
           lower = as.vector(imp$Lower$y),
           to = rep(c("y","x"),c(11,11))) %>% 
  ggplot(aes(x=rep(1:11,2),y=impluse))+
  facet_wrap(.~ to,nrow = 2)+
  geom_line(aes(color=to))+
  geom_ribbon(aes(ymax=upper,ymin=lower),alpha=0.2,linetype=2)+
  labs(title="From Y",x="lag")