第3回：RとPythonで学ぶデータサイエンス数学~線形回帰と最小二乗法~

前回までで、平均や分散、微分、偏微分の基本的なところを扱ってきました。

第3回となる今回は、今までの知識を使って統計、機械学習で最も基本的で、最も頻出の線形回帰と最小二乗法についてご紹介します。今回の目的は、以下になります。

偏微分を使って、関数の値を最小にするパラメーターを見つけることができる。
最小二乗法で、線形回帰モデルを作ることができる。

誰が読んでも理解できることを目指していますので、分かりにくい、理解できない等ありましたら、お気軽にコメント頂けると幸いです。なお、RやPythonを使わなくても、学ぶことができる内容ですので、数学の知識だけ学びたいという方も是非ご覧ください（^^）

メールの数と売上の関係
線形回帰と最小二乗法
偏微分で最小二乗法を解く
- Rで実践
- pyhonでの実践
補足：最小二乗法のもう一つの考え方
まとめ
参考

メールの数と売上の関係

ある企業は、顧客にメールで広告を送っています。そして、この企業が一人当たりに送ったメールの数と商品の売上について調べたデータがあるとしましょう。こんなデータになります。

mail	sales
1	12500
2	19700
3	29600
4	53700
5	47700
6	75200
7	54500
8	85800
9	91200
10	102200

#データの作成
mail <- seq(1,10)
sales <- c(12500,19700,29600,53700,47700,75200,54500,85800,91200,102200)
dt <- tibble(mail=mail,
                 sales = sales)

#データの作成
import numpy as np
import pandas as pd

mail = np.arange(1,11)
sales = np.array([12500,19700,29600,53700,47700,75200,54500,85800,91200,102200])

dt = pd.DataFrame({"mail":mail,
                 "sales":sales})

このデータを、横軸をメールの数、縦軸を売上として、グラフにしてます。

データサイエンス数学

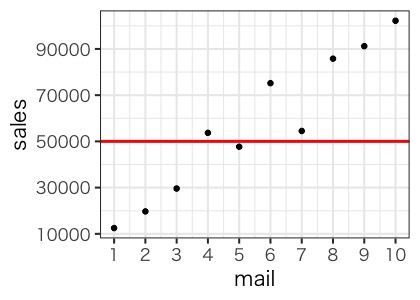
メールの数が増えると売上が増えるという関係性にありそうですね。さてそれでは、赤のラインである売上5万円を超えるためには、メールを何通送ればよいでしょうか？こんな線を引いてみます。

データサイエンス数学

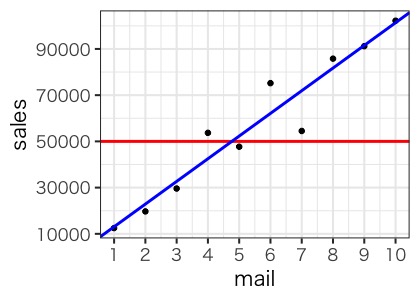
この線は、小中で習う、

$y=\beta_{1}+\beta_{2}x$

で表される切片 $\beta_{1}$ と傾き $\beta_{2}$ も持つ直線です。切片と傾きをa、bで表すこともありますが、データサイエンス領域では $\beta$ （ベータ）と表わすことが多いので、今後はこちらで書いていきます。この直線は見方を変えると、メールの数を入力値とし、売上が出力される関数とみなすこともできますね。この関数のことを線形回帰モデルと呼びます。

データサイエンス数学

ここで、

$実際の売上（実測値）：y \\関数の出力値（予測値）：\widehat{y}$

と表すことにします。 $\widehat{y}$ はyハットと呼び、多くの参考書でもでてくるので慣れておきましょう。

データサイエンス数学

線形回帰と最小二乗法

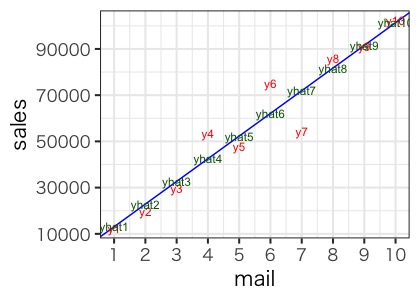
さて、線形回帰モデルを作るためには、すべてのデータから、なるべく近いところに線を引きたいですよね。これを実現するために、実測値 $y$ と予測値 $\widehat{y}{y}$ の距離をすべて足し合わせ、その値が1番小さくなるところに線を引くことにします。例えば、下の二つのグラフでは、1番目のグラフの方が $y$ （実測値）と $\widehat{y}$ （予測値）の距離が近く、当てはまりが良い線になっています。

データサイエンス数学

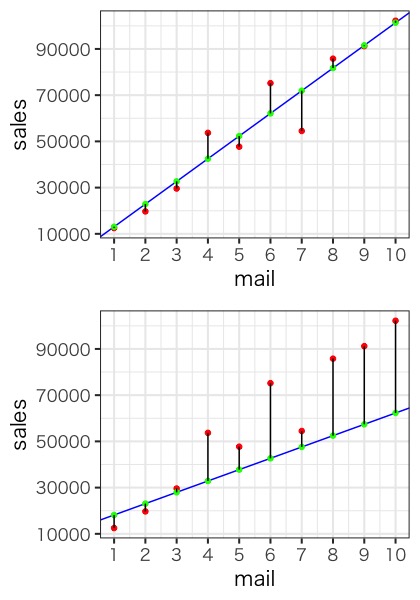
この実測値-予測値の値のことを残差とも呼びます。ここで、第一回目の記事で紹介した分散の考え方を使いましょう。実測値から予測値を引いた値である残差を二乗した値を足し合わせた平方和を最小にする $\beta_{1}, \beta_{2}$ を求めることで、線形回帰モデルを作ることができます。この平方和を最小にする方法が、最小二乗法です。

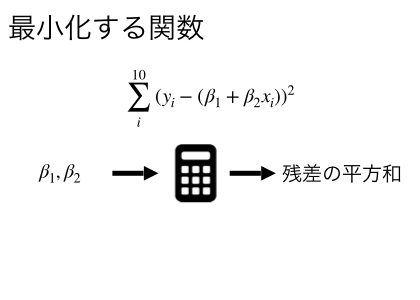
まずは、今までの知識を使って文字で表してみます。売上をy、メールの数をxとして、メールが1通の時の売上をy1と表わすことにします。すると平方和は、

$(y_{1}-\widehat{y}_{1})^{2}+(y_{2}-\widehat{y}_{2})^{2}+(y_{3}-\widehat{y}_{3})^{2}+\dots(y_{10}-\widehat{y}_{10}^{2})\\ =\sum_{i}^{10} (y_{i}-\widehat{y}_{i})^{2}$

と表されます。ここで

$\widehat{y}_{i} = \beta_{1} + \beta_{2}x_{i}$

なので、

$\sum_{i}^{10} (y_{i}-( \beta_{1} + \beta_{2}x_{i}))^{2}$

です。

これを最小にする $\beta_{1}$ と $\beta_{2}$ の値を求めれば、線形回帰モデルの完成です。このワード聞き覚えありませんか？そう！微分して傾きを0にするです！ちなみに上記のような、最小化を目指す関数を機械学習の世界では損失関数またはコスト関数とよぶこともあります。コスト関数を最小にすることは、予測値と実測値の差を最小にすることであると言い換えることもできます。

偏微分で最小二乗法を解く

ここで、微分の便利な性質を紹介します。微分は、それぞれの項を微分してから足しても、足してから微分しても、答えは同じになります。この性質を利用すると、シグマの入った式でも微分を行うことができます。それでは、実際に微分をしていきまょう。はじめに今回の損失関数を

$f(\beta_{1}, \beta_{2})) = \sum_{i}^{10} (y_{i}-( \beta_{1} + \beta_{2}x_{i}))^{2}$

と定義します。ここでの注意点は、メールの数であるxと、売上のyはすでに決まっており、変化するのは $\beta_{1},\beta_{2}$ です。この関数は $\beta_{1},\beta_{2}$ の値を入力すると、残差の平方和出力する関数であることに注意しましょう。

データサイエンス数学

とりあえずシグマの記号は無視して、前回ご紹介した合成関数の微分を使って中身だけを $\beta_{1}$ で偏微分します。

www.medi-08-data-06.work

$\beta_{1}で偏微分$

$\dfrac{\partial}{\partial \beta_{1}} f(\beta_{1}, \beta_{2})) = \sum_{i}^{10} (y_{i}-( \beta_{1} + \beta_{2}x_{i}))^{2}\\ = \sum_{i}^{10} 2(y_{i}- \beta_{1} - \beta_{2}x_{i})(-1)\\ = \sum_{i}^{10} -2y_{i}+2 \beta_{1}+2\beta_{2}x_{i}$

次にシグマをそれぞれの項に移動させ、yとxの実際の値を入れます。

$\sum_{i}^{10} -2y_{i}+2 \beta_{1}+2\beta_{2}x_{i}\\ = -2\sum_{i}^{10} y_{i}+ 2\sum_{i}^{10} \beta_{1}+ 2\sum_{i}^{10}\beta_{2}x_{i}\\ = -2(y_{1}+ y_{2}\dots+y_{10}) + 2\times 10\beta_{1} + 2\beta_{2}(x_{1}+ x_{2}\dots+x_{10})\\ =-1144200+20\beta_{1}+ 110\beta_{2}$

となります。同様に $\beta_{2}$ でも偏微分します。

$\beta_{2}で偏微分$

$\dfrac{\partial}{\partial \beta_{2}} f(\beta_{1}, \beta_{2})) = \sum_{i}^{10} (y_{i}-( \beta_{1} + \beta_{2}x_{i}))^{2}\\ = \sum_{i}^{10} 2(y_{i}- \beta_{1} - \beta_{2}x_{i})(-x_{i})\\ = \sum_{i}^{10} -2y_{i}x_{i}+2 \beta_{1}x_{i}+2\beta_{2}x_{i}^{2}\\ = -2\sum_{i}^{10} y_{i}x_{i}+ 2\sum_{i}^{10} \beta_{1}x_{i}+ 2\sum_{i}^{10}\beta_{2}x_{i}^2\\ = -2(y_{1}x_{1}+ y_{2}x_{2}\dots+y_{10}x_{10}) + 2\beta_{1}(x_{1}+ x_{2}\dots+x_{10}) + 2\beta_{2}(x_{1}^{2}+ x_{2}^{2}\dots+x_{10}^{2})\\ =-7911800+110\beta_{1}+ 770\beta_{2}$

ここまでこれば、あとは二つの式をイコール０とした連立方程式を解けば良いので、

$\left\{ \begin{array}{l} -1144200 + 20\beta_{1}+110\beta_{2} = 0 \\ -7911800 + 110\beta_{1}+770\beta_{2} = 0 \\ \end{array} \right.$

$\beta_{1} \fallingdotseq 3253\\ \beta_{2} \fallingdotseq 9810$

となって、回帰モデルは

$\widehat{y} = 3253+9810x$

となります。ここから売上が5万を超えるためには、

$3253+9810x =50000\\ x \fallingdotseq 4.7$

となるので、メールを5通以上配信すれば、売上が５万を超えることが期待されることが分かりますね。これが最小二乗法使った線形回帰モデルの作り方です。実は機械学習では、最急降下法という別のアルゴリズムを使うことが多いのですが、詳細については、以前記事にしたので、気になる方はそちらをご覧ください。

www.medi-08-data-06.work

Rとpythonでの実践は、前回同様に連立方程式を使っても良いのですが、損失関数を最小化していることを意識しやすいようにしてみましょう。

Rで実践

Rで任意の関数を最小化するパラメーターを求めるにはoptimを使います。

www.medi-08-data-06.work

#損失関数を定義する
fbeta <- function(beta){
  return(sum((sales-beta[1]-beta[2] * mail)^2)) 
}

# 最小化を目指す
res <- optim(c(0,10000),fbeta)
print(res$par)

>[1] 3253.721 9810.183

pyhonでの実践

pythonでは、scipyのoptimizeを使います。

#損失関数を定義する
import scipy as sp

def fbeta(beta):
    return np.sum((sales-beta[0]-beta[1] * mail)**2)

#最小化を目指す。
res = sp.optimize.fmin(fbeta, [0,0])
print(res)]

>array([3253.33337036, 9810.30301821])

補足：最小二乗法のもう一つの考え方

今回は $y - \widehat{y}$ で表される残差の平方和を最小にする方法を用いました。線形回帰モデルの説明のされ方にはこのような表現も出てきます。

$y_{i} =\beta_{1} + \beta_{2}x_{i} + \epsilon_{i}$

$\epsilon_{i}$ はイプシロンと呼ばれるもので、誤差を表すときに用いられる数学記号です。この式は、実測値は、 $\beta_{1} + \beta_{2}x_{i}$ で表される線形回帰モデルの推定値（つまり $\widehat{y}$ ）に、誤差を足したものである、ということをあらわています。そして、式を少しだけ変形すると、

$\epsilon_{i} =y_{i} - (\beta_{1} + \beta_{2}x_{i})$

とすることが出来ます。そして、誤差の平方和が最小になるパラメータを求めるというのが、最小二乗法のもう一つの考え方です。どっちにしろ同じ結果になりますが、こちらの書き方で記載されることもありますので、覚えておきましょう。また、誤差と残差の違いについては、統計学で言うところの母集団の推定の概念が必要ですので、ここでは割愛させて頂きます。