ベイズで考える状態空間モデル - 医療職からデータサイエンティストへ

古典的な時系列解析のモデルでは、時系列データが定常過程に従うことを前提としていました。しかし、世の中の多くの事象は定常過程に従うことはあまりなく、よりうまく現実を反映させることができるモデルが必要になります。

それが状態空間モデルです。状態空間モデルは今まで紹介してきたARIMAモデルなどの進化版とも言えて、古典的なモデルを含む多くのモデルを一つの概念で捉えることができます。

さらに、他の変数からの影響や周期性なども柔軟に組み込むことができるとても素晴らしいモデルになります。

状態空間モデルの直感的な説明などは多くのサイト様で紹介されているので、今回はベイズ流で状態空間モデルを考えていきたいと思います。

www.medi-08-data-06.work

うっかり店長さんの売り上げデータ

あるお店の売り上げ100日間のデータを解析することにしましょう。まずは単純なモデルから考えるため、以下のような前提をおきます。

お店の売り上げにトレンドはない。
お店の売り上げは前日の売り上げと似ている（急激に増減しない）。
売り上げデータは店長さんが毎日手入力するため誤差が生じる。
店長さんのうっかり誤差は5万円ぐらい。
店長さんは、経験的に売り上げは平均20万、日による変動は3万ぐらいだと言っている。

グラフにしてみるとこんな感じです。

状態空間

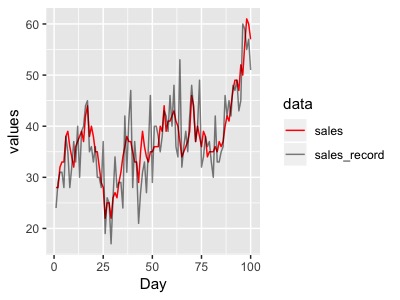
また、真の売り上げを $x_{t}$ 、記録された売り上げを $y_{t}$ とすると

$x_{t} = x_{t-1}+w_{t}\,\, w\sim N(0,\sigma_{w}^{2}=3^{2})\\ y_{t} = x_{t} + v_{t}\,\, v\sim N(0,\sigma_{v}^{2}=5^{2})$

と表すことができると仮定します。売り上げの変動と店長さんの記録誤差は正規分布を仮定しました。日本語で書くと

$真の売り上げ = 前日の売り上げ+変動 \,\, 変動は平均0、分散9の正規分布に従う。\\ 記録された売り上げ = 真の売り上げ + 記録誤差\,\, 記録誤差は平均0、分散25の正規分布に従う。$

です。

ここでやりたいのは、店長さんが記録したデータ（y:黒）から、真の売り上げ（x:赤）の分布を推定することです。

推定方法

真の売り上げを推定するための考え方としては、売り上げ $y_{t}$ が観測された場合に、真の値が $x_{t}$ となる確率として求めます。ベイズの基本的なところはこちらをご覧ください。

www.medi-08-data-06.work

1日目の売り上げから順を追って解析していきましょう。少し数式が多くなるので、下の方に直感的なイメージ図を書きました。そちらから見てみると良いかもしれません。

1日目のデータ $y_{1}$ から、ベイズ更新を使って $x_{1}$ の分布を以下のように求めます。

$p(x_{1}\,|\,y_{1}) \propto 尤度\times 事前分布\\ = p(y_{1}|x_{1})\times p(x_{1})$

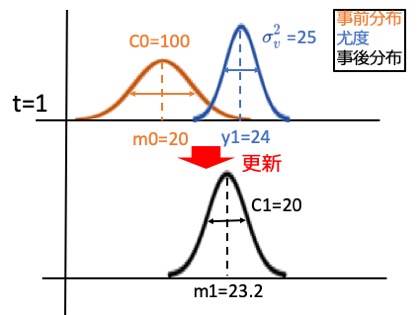
事前分布 $p(x_{1})$ は、正規分布を仮定します。店長の経験から売り上げは平均m0=20ですが、うっかり店長のことなので間違っていることを考慮して、その不確かさをC0=100としておきます。これを平均20、標準偏差10の正規分布であると考えると $x_{1}$ となる確率は

$p(x_{1}) = \dfrac{1}{\sqrt{2\pi C0}}exp\left\{-\dfrac{(m0-x_{1})^{2}}{2C0}\right\}$

となります。（具体的な計算は後ほど行います。）

また、尤度 $p(y_{1}|x_{1})$ は、真の売り上げが $x_{1}$ であった場合に、売り上げ記録が $y_{1}$ となる"もっともらしさ"を表し、店長さんの記録誤差 $\sigma_{v}^{2}=5^{2}$ を分散、平均を $x_{1}$ とする正規分布に従うとすると、

$p(y_{1}|x_{1}) = \dfrac{1}{\sqrt{2\pi \sigma_{v}}}exp\left\{-\dfrac{(x_{1}-y_{1})^{2}}{2\sigma_{v}^{2}}\right\}$

です。

以上から事後分布である $p(x_{1}\,|\,y1)$ を求めると

$p(x_{1}\,|\,y_{1}) \propto \dfrac{1}{\sqrt{2\pi \sigma_{v}}}exp\left\{-\dfrac{(x_{1}-y_{1})^{2}}{2\sigma_{v}^{2}}\right\}\times \dfrac{1}{\sqrt{2\pi C0}}exp\left\{-\dfrac{(m0-x_{1})^{2}}{2C0}\right\}$

となります。ここで、興味があるのは $x_{1}$ なので、関係のない部分は無視して、

$\propto exp\left\{-\dfrac{(x_{1}-y_{1})^{2}}{2\sigma_{v}^{2}}-\dfrac{(m0-x_{1})^{2}}{2C0}\right\}\\ =exp\left\{-\dfrac{x1^{2}-2x_{1}y_{1}+y_{1}^{2}}{2\sigma_{v}^{2}}-\dfrac{m0^{2}-2x_{1}m0+x_{1}^{2}}{2C0}\right\}\\ \propto exp\left\{-\dfrac{x_{1}^{2}-2x_{1}y_{1}}{2\sigma_{v}^{2}}-\dfrac{-2x_{1}m0+x_{1}}{2C0}\right\}\\ = exp\left\{-\dfrac{1}{2C0\sigma^{2}}((C0+\sigma_{v}^{2})x_{1}^{2}-2(y_{1}C0+m0\sigma_{v}^{2})x_{1})\right\}\\ = exp\left\{-\dfrac{C0+\sigma_{v}^{2}}{2C0\sigma^{2}}(x_{1}^{2}-2\dfrac{y_{1}C0+m0\sigma_{v}^{2}}{C0+\sigma_{v}^{2}}x_{1})\right\}$

また事後分布から考えると $x_{1}$ は平均m1、標準偏差C1の正規分布に従うので、

$p(x_{1}\,|\,y_{1}) \propto exp\left\{\dfrac{1}{2C1}(x_{1}^{2}-2m1x_{1})\right\}$

となります。以上から

$m1 = \dfrac{y_{1}C0+m0\sigma_{v}^{2}}{C0+\sigma_{v}^{2}}\\ = \dfrac{C0}{C0+\sigma_{v}^{2}}y_{1}+\dfrac{\sigma_{v}^{2}}{C0+\sigma_{v}^{2}}m0$ $C1 = \dfrac{C0\sigma_{v}^{2}}{C0+\sigma_{v}^{2}}$

ここに1日目の記録売り上げが24万であるとして、具体的に計算してみると

$m1 = \dfrac{C0}{C0+\sigma_{v}^{2}}y_{1}+\dfrac{\sigma_{v}^{2}}{C0+\sigma_{v}^{2}}m0\\ = \dfrac{100}{100+25}\times 24+\dfrac{25}{100+25}\times 20\\ = 0.8\times 24 + 0.2\times 20\\ =23.2$

$C1 = \dfrac{C0\sigma_{v}^{2}}{C0+\sigma_{v}^{2}}\\ = \dfrac{100 \times 25}{100+25}\\ = 20$

となります。つまりt=1時点の真の売り上げは平均23.2万、標準偏差4.5万(20の平方根)の分布であることが分かります。この事後分布の平均値が状態の点推定値になります。

ついでにt=2時点の分布も求めてみましょう。まずはt =2時点の平均と分散を予測します。今回は売り上げにトレンドなどがないため、t=2時点の予測値は

$\hat{m2} = E(m1+w_{t}) = m1 = 23.2$

です。分散は売り上げ変動の影響を考慮して、

$\hat{C2} = Var(m1+w_{t}) = C1+\sigma_{w}^{2}=20+9=29$

となります。これを事前分布として、2日目の記録売り上げが29万だとすると、

$m2 = \dfrac{\hat{C2}}{\hat{C2}+\sigma_{v}^{2}}y_{2}+\dfrac{\sigma_{v}^{2}}{\hat{C2}+\sigma_{v}^{2}}\hat{m2}\\ = \dfrac{29}{29+25}\times 29+\dfrac{25}{29+25}\times 23.2\\ = 26.4$ $C2 = \dfrac{\hat{C2}\sigma_{v}^{2}}{\hat{C2}+\sigma_{v}^{2}}\\ = \dfrac{29 \times 25}{29+25}\\ = 13.4$

となって、t=2時点では平均26.4万、標準偏差3.6万円の分布に更新されました。式だと分かりにくいので、図にしてみましょう。

状態空間

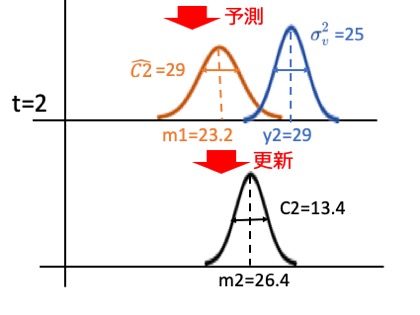
式からもわかるように、事前分布の平均、つまり一期前で推定された値と観測された値とを、事前分布の分散と尤度の分散の加重平均をして、事後分布の平均値を求めているイメージです。

これを繰り返して真の売り上げを推定したものが以下になります。

状態空間

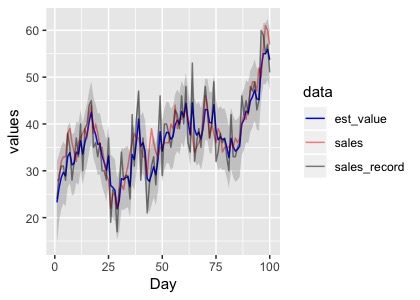
青色が記録データから推定した真の状態、網掛けが状態の95％信頼区間を表しています。真の売り上げをうまく推定できているみたいですね。

ちなみに今回のように状態がランダムウォークに従い、観測誤差があるモデルのことをランダムウォークプラスノイズモデル、またはローカルレベルモデルと呼びます。

ちなみに先ほどの式を少し変換して、

$m1= \dfrac{C0}{C0+\sigma_{v}^{2}}y_{1}+\dfrac{\sigma_{v}^{2}}{C0+\sigma_{v}^{2}}m0\\ = \dfrac{C0}{C0+\sigma_{v}^{2}}y_{1}+(1-\dfrac{C0}{C0+\sigma_{v}^{2}})m0\\ = mo+\dfrac{C0}{C0+\sigma_{v}^{2}}(y1-m0)$

$C1 = \dfrac{C0\sigma_{v}^{2}}{C0+\sigma_{v}^{2}}\\ = (1-\dfrac{C0}{C0+\sigma_{v}^{2}})C0$

としてみると、カルマンフィルターの式になりました。このようにして、状態空間モデルをベイズ的に捉えることができます。

Rでの実践

Rで状態空間モデルを扱うにはいくつか方法がありますが、今回は一番ポピュラーな{dlm}を使った方法で行なっていきます。まずは今回のデータを作成します。

set.seed(123)
sales <- 30+round(cumsum(rnorm(100,0,3)),0)#真の売り上げ
sales_record <-round(sales+rnorm(100,0,5),0)#記録売り上げ

data <- tibble(sales_record=sales_record,
                     sales=sales,
                     Day=seq(1,100))

#可視化
data %>%
  gather(key=data,value = values,-Day) %>% 
  ggplot()+
  geom_line(aes(x=Day,y=values,col=data,alpha=data))+
  scale_color_manual(values = c("red","black"))+
  scale_alpha_manual(values = c(1,0.5))

続いて{dlm}をインストールして読み込みます。

install.packages("dlm")
library(dlm)

今回は詳しく扱いませんが、{dlm}は

モデルを作る
パラメーターを推定する
フィルタリングする
平滑化する

という流れで状態の推定を行います。3.のフィルタリングが今回のメインである逐次更新の部分です。また、2のパラメーターの推定は、今回は既知として扱った状態の変動（売り上げの変動： $\sigma_{w}^{2}$ )と観測誤差（記録の誤差： $\sigma_{v}^{2}$ ）を最尤法で推定することができます。また、平滑化とはフィルタリング後のデータを使って過去の状態を推定し直すのですが、今回はそこまでやりません。

それではやっていきましょう。

fit <-  dlmModPoly(order=1,
           dV=25,
           dW=9,
           m0=20,
           C0=100)

fit_filter <- dlmFilter(sales_record,fit)

まずは、dlmModPolyで、ローカルレベルモデルを作成します。ここには他にも色々なモデルを指定することができます。dVが観測誤差、dWが状態の変動、m0、C0が事前分布の平均と分散です。そして、dlmFilterで状態を推定できます。

fil_filterの中身を見てみましょう。

str(fit_filter,max.level = 1)

List of 9
 $ y  : num [1:100] 24 29 31 31 28 38 35 28 32 37 ...
 $ mod:List of 10
  ..- attr(*, "class")= chr "dlm"
 $ m  : num [1:101] 20 23.3 26.4 28.6 29.7 ...
 $ U.C:List of 101
 $ D.C: num [1:101, 1] 10 4.51 3.67 3.44 3.37 ...
 $ a  : num [1:100] 20 23.3 26.4 28.6 29.7 ...
 $ U.R:List of 100
 $ D.R: num [1:100, 1] 10.44 5.42 4.74 4.57 4.51 ...
 $ f  : num [1:100] 20 23.3 26.4 28.6 29.7 ...
 - attr(*, "class")= chr "dlmFiltered"

yには元のデータが格納されています。フィルタリング後のデータはmに格納され、これが事後分布の平均値です。データが101あるのは、0時点目の初期値が含まれているからです。20 23.3 26.4....と続き、先ほど計算した値とも合っていますね。

続いてU.CとD.Cは事後分布の分散になります。二つに分かれている理由については少し複雑な話になるのですが、分散の特異値分解後の値になっているからです。この二つを使って元の分散に戻し、95%信頼区間などを算出できます。dlmSvd2varを使って特異値分解された分散を元に戻します。

conf <- sqrt(as.numeric(dlmSvd2var(fit_filter$U.C,fit_filter$D.C)[-1]))
> conf[1:5]
[1] 4.509526 3.673889 3.441134 3.371355 3.350101

こちらも先ほどの同じ値になっています。

その下のa,U.R,D.Rは、事後分布から次の時点を予測した事前分布の平均と分散を表します。

推定したデータをグラフにしてみましょう。

data <- tibble(sales_record=sales_record,
                     sales=sales,
                     Day=seq(1,100),
               est_value = fit_filter$m[-1],
               upp = est_value+qnorm(0.025,0,sd=conf),
               low = est_value+qnorm(0.975,0,sd=conf))

data %>%
  gather(key=data,value = values,-Day,-upp,-low) %>% 
  ggplot()+
  geom_line(aes(x=Day,y=values,col=data,alpha=data))+
  geom_ribbon(aes(x=Day,ymax=upp,ymin=low),alpha=0.2,linetype=3)+
  scale_color_manual(values = c("blue","red","black"))+
  scale_alpha_manual(values = c(1,0.5,0.5))