医療職からデータサイエンティストへ

統計学、機械学習に関する記事をまとめています。

トップ > 機械学習 > 初歩からの機械学習〜ベイズ識別規則と混同行列〜

初歩からの機械学習〜ベイズ識別規則と混同行列〜

機械学習 ベイズ

ベイズとは条件付き確率を表すのにとても有用な概念で、統計学だけでなく機械学習にも応用されています。特にクラス分類では、ある変数の情報が入ってきたときに、それがあるクラスに属する確率としてベイズの考えが利用され、迷惑メールフィルターの基礎的な部分などにも用いられます。

今回はそんなベイズを使った機械学習におけるクラス分類の基礎事項と、クラス分類の性能評価に用いられる混同行列も合わせて紹介していきます。基礎的なところから書いていくので、すでにご存知の方は適宜読み飛ばしてください。

ベイズの基礎事項

ベイズの基礎部分は、様々なところでわかりやすい解説がなされているので、この記事では基礎的な用語の紹介に留めておきます。まず、よく見るベイズの式は以下のようなものです。

連続型： p( C | x) = \dfrac{p( x | C)p(C)}{\int p(x|C)p(C)} = \dfrac{p( x | C)p(C)}{p(x)}

離散型： p( C | x) = \dfrac{p( x | C)p(C)}{\sum p(x|C)p(C)} = \dfrac{p( x | C)p(C)}{p(x)}

これを少し書き換えて

p( C | x) = \dfrac{p( x | C)p(C)}{p(x)}=\dfrac{p( x | C)}{p(x)}\times p(C)

とすると、もともと確率がp(C)だったものに、\dfrac{p( x | C)}{p(x)}をかけることで確率が p( C | x)に更新されることを表しています。日本語で書くと、

\small 値がxの時、クラスCに属する確率 = \\ \small\dfrac{クラスCに属するときに、値がxになる確率}{値がxになる確率}\timesクラスCに属する確率

となります。このとき、クラスCに属する確率p(C)を事前確率、 値がxの時、クラスCに属する確率p(C|x)を事後確率、真ん中の項を修正項と呼びます（事前確率を事後確率に修正するイメージです）。

ベイズの基礎知識に関しては、こちらの書籍がとてもわかりやすくておすすめです。

基礎からのベイズ統計学: ハミルトニアンモンテカルロ法による実践的入門

基礎からのベイズ統計学: ハミルトニアンモンテカルロ法による実践的入門

ベイズ識別規則

ベイズの定理をなんとなく理解したところで、これをどのようにクラス分類の応用するのかというのはとても簡単で、ズバリ事後確率がもっとも大きくなるクラスに分類します。例えば、ある商品を購入するかどうかは年齢のみが要因として作用するとしましょう。ここでは話を簡単にするため、年齢を離散値として扱い、高齢者or若者の2値とします。

購買データを調べ、商品の購入の有無を調べると以下のようになっていました。

ベイス識別

ここからベイズ識別規則を使って、高齢者（x=1）であった場合に商品を買うかどうかを求めてみます。まず、年齢の情報が与えられていないときに商品を買う確率、つまり事前確率p(C)は

p(C =0) = \dfrac{700}{1400} =\dfrac{1}{2}

p(C =1) = \dfrac{700}{1400} =\dfrac{1}{2}

となります。次に商品を買った場合or買わなかった場合に高齢者である確率（修正項の分子）を求める と

p(x=1 | C=1) = \dfrac{300}{700} =\dfrac{3}{7}

p(x=1 | C=0) = \dfrac{200}{700} =\dfrac{2}{7}

となります。さらに、高齢者である確率（修正項の分母）は

p(x) = p(x=1 | C=1)p(C=1)+p(x=1 | C=0)p(C=0) = \dfrac{300}{700}\times\dfrac{1}{2}+\dfrac{200}{700}\times\dfrac{1}{2} = \dfrac{5}{14}

となります。ちなみに修正項の分子を尤度、修正項の分母を周辺確率とも呼びます。 以上からそれぞれの事後確率を求めると

p(C=1 | x=1) = \dfrac{3}{7}\times\dfrac{14}{5} \times\dfrac{1}{2} = 0.6

p(C=0 | x=1) = \dfrac{2}{7}\times\dfrac{14}{5} \times\dfrac{1}{2} = 0.4

となるので、高齢者という情報が与えられた場合は商品を購入するクラス（C=1）に分類されることになります。これがベイズ識別規則というものです。このように事後確率が大きくなるクラスに分類するのですが、よくみてみると周辺尤度はどちらにも共通しているので、これは考慮しなくても良さそうです。以上から式でまとめるとベイズ識別規則は

識別クラス = arg\, max_{i} p(x |C_{i})p(C_{i})

と表すことができます。arg maxは難しそうに見えますが、単に尤度×事前確率の値が大きくなる方のiに分類するという意味です。今回の場合はi=0の時より、i=1の時の方が値が大きくなったため、i=1に分類されることになります。

連続量の予測モデル

先ほどは簡単にするために年齢を2値としましたが、もう少し実用的にするために年齢を連続量に置き換えて、ベイズ識別規則によるモデル作ってみましょう。 まず、仮想的に以下のような1000人の購買データがあったとします。

class age
0 26
0 29
0 25
0 30
0 29
0 24

classは買ったかどうか（それぞれ500人ずつ）、ageは年齢です。これをclassで色分けしてヒストグラムにしてみます。

ベイス識別

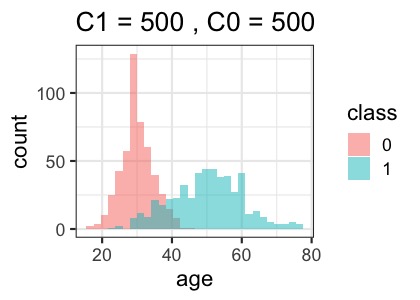
ここでやりたいことはベイズ識別規則を使って、その人がどちらのクラスに分類されるか、つまり購入するかどうかを予測するモデルを作成します。まず30歳の人がどちらに分類されるか計算してみましょう。

まず、年齢の情報が与えられていないときに商品を買う確率、つまり事前確率p(C)は

p(C =0) = \dfrac{500}{1000} =\dfrac{1}{2}

p(C =1) = \dfrac{500}{1000} =\dfrac{1}{2}

となります。次に商品を買った場合or買わなかった場合に30歳である確率を求める と

p(x=30 | C=1) = \dfrac{43}{500}

p(x=30 | C=0) = \dfrac{3}{500}

となります。それぞれのクラスで尤度×事前確率の値を求めてみると

p(x=30 | C=1)p(C=1) = \dfrac{43}{500}\times\dfrac{1}{2} = 0.003

p(x=30 | C=0)p(C=0) = \dfrac{3}{500}\times\dfrac{1}{2} = 0.043

となりました。ベイズ識別規則のルールに従うとC=0の方が値が大きいため、年齢30歳の人は購買なしに分類されます。このようにして30歳から40歳まで人がどちらに分類されるかを表したのが以下になります。

age p(x|c1)*p(c1) p(x|c0)*p(c0) pred_class
30 0.003 0.043 0
31 0.009 0.039 0
32 0.003 0.040 0
33 0.005 0.028 0
34 0.004 0.032 0
35 0.011 0.020 0
36 0.010 0.020 0
37 0.004 0.012 0
38 0.014 0.014 0
39 0.011 0.007 1
40 0.011 0.008 1

38歳までは購買なしに分類され、それ以上になると購買ありに分類されるモデルとなっているようです。（38歳は値が同じであるため、リジェクトといって分類不可とすることもできます。）

ちなみに機械学習クラス分類モデルには、予測の方法の違いからいくつかの種類に分けられ、ベイズ識別規則によるものは識別モデルに分類されます。その他の分類に関しては、下記記事をご覧ください。

www.medi-08-data-06.work

混同行列による性能評価

さて、クラス分類で問題となるのは、誤って分類してしまう可能性もあるというところです。例えば、今回の場合は39歳以上という情報が与えられた場合は購買あり(C=1)に分類されてしまうため、39歳以上で購買なしの方たちは誤って分類されてしまいます。このように作成したモデルを評価するために用いられるのが、混同行列(confusion matrix)です。混同行列はクラス分類の機械学習モデルの性能評価によく用いられます。

混同行列とは以下のようなものです。

ベイス識別

Trueとは正しく分類したという意味で、Positiveとは購買ありのクラスという意味です。つまり、真陽性(True Positive)とは、購買ありの人を正しく分類したという意味となります。ややこしいですが、True or False、Positive or Negativeを一つずつ見ていけば理解できるかと思います。

この混同行列からよくクラス分類の機械学習評価指標で用いられる正確度（accuracy）という指標を求めることができます。正確度は以下のように計算されます。

正確度＝(TP＋TN)/(P+N)

Pは購買あり（Positive）の数、Nは購買なし(Negative)の数です。P+Nとはつまり、サンプル数のことです。正確度は、全サンプルの中で正しく分類されたサンプルの割合という意味です。今回のモデルの場合の混同行列は以下のようになります。

ベイス識別

ここから正確度を計算すると

(418+482)/1000 = 0.9

となりました。つまり、データの90％をこのモデルで正しく予測できることになります。これが現実世界のデータセットを使ったモデルならかなり良い結果ですね。ただし、テストデータではなくトレーニングデータの結果であることには注意が必要です。

混同行列を使ったその他の指標

混同行列からは、正確度の他にも、様々な評価指標を計算することができます。 まずは、医療でもよく用いられるこの二つです。

  • 感度（真陽性率）： 陽性の人を正しく陽性だと判断する確率 TP/(TP+FN)
  • 特異度（真陰性率）：陰性の人を正しく陰性だと判断する確率 TN/(TN+FP)

一見同じに見えますが、この二つはトレードオフの関係となります。例えば、購買ありに分類される年齢を20歳以上とするとどうでしょうか？この場合の混同行列をみてみます。

ベイス識別

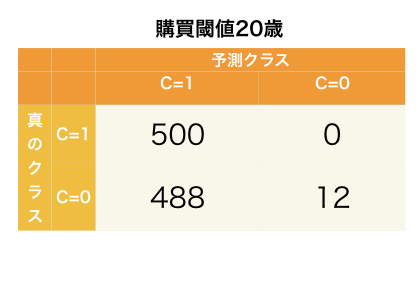
ここから感度・特異度を計算してみると

感度：500/500 = 1

特異度：12/500 = 0.024

1000人中、ほとんどの人が購買ありと分類されるため、購買ありの人を正しく購買ありと判断する確率はほぼ100％となります。しかし、購買なしの人もほとんどが購買ありに分類されているため、購買なしの人を正しく分類できていません。

逆に年齢の閾値を60歳にしてみると結果は以下のようになります。

ベイス識別

感度：67/500 = 0.134

特異度：500/500 = 1

この場合、特異度は高くなりますが、感度は低くなります。このように感度・特異度はトレードオフの関係にありますが、モデルによってはどちらも100％に近づけることも可能です。今回の例では変数が年齢しかないため、どちらも100％とまではいきませんが、ベイズ識別規則ではこの二つが最大になるところに閾値が設定されます。試しに、ベイズ識別規則で示された39才を閾値として感度、特異度を求めてみると

感度：418/500 = 0.836

特異度：482/500 = 0.964

どちらも高いことが分かりますね。ただし、購買する可能性のある人を出来るだけ逃したくないと思えば、多少特異度を犠牲にしても感度が高くなる閾値に設定したモデルにすることもできますし、逆もまた然りです。ベイズ識別規則においては、損失行列というものを用いてそれぞれのクラスに損失の重み付けをすることで、感度・特異度の非対称性を実現できます。詳しくは扱いませんが、気になる方はこちらをご参照ください。

はじめてのパターン認識

はじめてのパターン認識

その他機械学習の分類問題で使われる指標としては、以下の二つがあります。

  • 適合率：陽性だと判断した人の中で、本当に陽性である確率 TP/(TP+FP)
  • 再現率：全体の中で、陽性の人を見つけられる確率 TP/(TP+FN)

再現率は感度と式は同じですが、意味合いが異なります。そして、適合率と再現率もトレードオフの関係であると言えます。ただし、感度、特異度、適合率、再現率の関係性については理解が進んでおらず、曖昧なことしか書けないので、ここでは紹介に程度に留めておきます。m(__)m

まとめ

今回はクラス分類の基礎であるベイズ識別規則と混同行列を紹介しました。クラス分類の機械学習手法はまだまだたくさんあるので、そのうちにご紹介していきます。混同行列は目的に合わせて指標を使い分ける必要があるので、よく理解しておきたいところです。

※本記事は筆者が個人的に学んだことをまとめた記事なります。所属する組織の意見・見解とは無関係です。また、数学の記法や詳細な理論、用語等で誤りがあった際はご指摘頂けると幸いです。

参考書籍

基礎からのベイズ統計学: ハミルトニアンモンテカルロ法による実践的入門

基礎からのベイズ統計学: ハミルトニアンモンテカルロ法による実践的入門

はじめてのパターン認識

はじめてのパターン認識

今回のRコード

library(tidyverse)
theme_set(theme_bw(base_size = 16))

#データセットの作成
set.seed(123)
C0 <- round(rnorm(30,5,n=500),0)
C1 <- round(rnorm(50,10,n=500),0)

d <- tibble(class=as.character(rep(c(0,1),c(500,500))),
       age = c(C0,C1)) 

#ベイズ識別規則に基づく関数
bayes_f <- function(age){
  #購買する確率（事前確率）
  p_c1 <- sum(d$class==1)/1000
  p_c0 <- sum(d$class==0)/1000
  
  #購買クラスの中でその年齢になる確率(尤度)
  p_x_c1 <- sum(d$class==1&d$age==age)/sum(d$class==1)
  p_x_c0 <- sum(d$class==0&d$age==age)/sum(d$class==0)
  
  #尤度*事前確率
  c("p(x|c1)*p(c1)"=(p_x_c1*p_c1),
  "p(x|c0)*p(c0)"=(p_x_c0*p_c0))
}

#30から40歳までの尤度*事前確率とその予測クラスを求める
map(seq(30,40),bayes_f) %>% 
  unlist() %>% 
  matrix(ncol=2,byrow = T) %>% 
  as_tibble() %>%
  mutate(age=seq(30,40),
         pred_class = ifelse(V1>V2,1,0)) %>%
  select(age,V1,V2,pred_class) %>% 
  rename("p(x|c1)*p(c1)"=V1,
         "p(x|c0)*p(c0)"=V2)

#混合行列を求めるための処理

thres <- 39 #閾値
confusion <- d %>% 
  mutate(pred_class = ifelse(age>thres,1,0)) %>% 
  mutate(TP = ifelse(class==1&pred_class==1,1,0),
         FN = ifelse(class==1&pred_class==0,1,0),
         FP = ifelse(class==0&pred_class==1,1,0),
         TN = ifelse(class==0&pred_class==0,1,0)
        ) %>% 
  summarise_at(.vars = vars(TP,FP,TN,FN),.funs = funs(sum))

matrix(c(confusion$TP,confusion$FP,confusion$FN,confusion$TN),ncol=2)