AICとは？その正体に迫る - 医療職からデータサイエンティストへ

複数のモデル候補があった場合、AIC（赤池情報量基準）を使ってモデル選択をすることがあります。しかし、このAICをなんとなく使ってしまっている人、そのモデル本当に目的としたモデルですか？

今回は、AICについてその直感的な理解とAICの意味を追っていきます。Rでの実行法については、記事下にまとめてあります。

AICの直感的理解
AICの意味とは？
- 少し脱線します
- 改めて見つめるAIC
まとめ
参考
今回のRソースコード

AICの直感的理解

そもそもAICとは、値が小さいモデルが良いモデルとされて、stepwiseなどでもモデルを選択する際に利用される指標です。例えば、

ある目的変数yに対する重回帰モデルを、説明変数候補を変えて複数作ったとします。さて、どのモデルが一番目的変数yに対するモデルとして適切なのでしょうか？

といった場合に用いられます。AICは式で書くと

$AIC= -2log(L(x | \theta ))+2p$

となります。この式の $log(L(x | \theta ))$ はモデルの対数尤度、つまりパラメーターが $\theta$ だった場合にxとなるもっともらしさ、pはパラメーターの数を表しています。尤度や対数尤度についてはこちらをご覧ください。

www.medi-08-data-06.work

直感的なイメージとしては、モデルのパラメーターが多ければ多いほど対数尤度は大きくなる（モデルを作ったデータyに対する説明力が上がる）ので $-2log(L(x | \theta )$ の部分は小さくなります。そこにパラメーターの数を足すことで、パラメーターを増やしすぎてもAICが小さくならないように調整しているというイメージです。

一般的には、機械学習でいう所の罰則項のように感じますが、実はこのAIC、全く違う理論から導出されています。

AICの意味とは？

さて、具体的な導出方法は後回しにして、とりあえずAICとはどんな意味を持つのかを探っていきましょう。先ほどAICが小さいモデルは適切であると書きました。ここで一つの疑問が生まれます。そもそも何をもって適切と判断しているのでしょうか？そこを探ることでAICの正体に迫ることができそうです。今回の内容はこちらを参考にしています。

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)

作者:久保拓弥
岩波書店

Amazon

少し脱線します

ひとつ例をあげてみます。

表と裏の出る確率がちょうど0.5であるコインがあります。しかし、あなたはこのコインの表と裏の出る確率を知りません。そこで、コインを50回投げて表の出た数からその確率を推定することにしたので、実際にやってみると表が40回でました。

ここから確率を40/50=0.8として、表が40回出るもっともらしさ、つまり対数尤度を求めてみましょう。コインの表がでる回数は二項分布に従うので、二項分布の式から対数尤度は以下のように導出します。

www.medi-08-data-06.work

$Bin(m|N,\theta)= {}_N C _m \theta^{m}(1-\theta)^{N-m}\\ log(Bin(m|N,\theta)) = log({}_N C _m \theta^{m}(1-\theta)^{N-m})\\ =log({}_N C _m)+log(\theta^{m}) + log(1-\theta)^{N-m})\\ =log({}_N C _m)+mlog(\theta) + (N-m)log(1-\theta)$

Nは試行回数、 $\theta$ は表の出る確率、 $m$ は表のでた回数を表します。

$\theta = 0.8,N=50,m=40$ として対数尤度を求めると

$log({}_{50} C _{40})+40log(0.8) + (50-40)log(1-0.2)=-1.96$

となります。つまり、表の出る確率が0.8のコインを50回投げて表が40回出るもっともらしさは-1.96ということです。対数尤度は絶対的な大きさに意味はなく、相対的に比べるものなので、試しに $\theta$ を0.1~0.9まで変化させて対数尤度をプロットしてみると

AIC

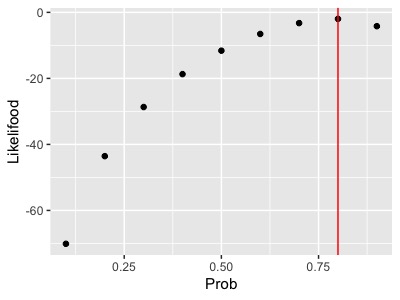
となって、 $\theta=0.8$ とするのがもっともらしいということになります。最尤法で求めた $\theta$ は得られたサンプルの期待値となるので、当然と言えば当然ですね。しかし、たまたま表が40回でるという驚異的なことが起こったため $\theta=0.8$ とするモデルがもっともらしくなりましたが、実際は25回前後ぐらい表が出るのが普通です。

そこで、このモデルの性能を測るために、先ほどのコイン(真の確率は $\theta=0.5$ )を50回投げて、表の回数と $\theta=0.8$ から、対数尤度を計算するということを100回ぐらい繰り返してみます。その対数尤度の平均値をみてみれば、この $\theta=0.8$ モデルがどれぐらいもっともらしいか分かりそうです。

この試行を繰り返してみると図のヒストグラムのような結果になり、対数尤度の平均値は-14となりました。

AIC

つまり、 $\theta=0.8$ モデルはサンプルされたデータに対する対数尤度は大きいですが、新たな試行に対してはそんなにもっともらしくないため、対数尤度を過剰に見積もっていることが分かります。

さて、それではサンプルされたデータから求まる対数尤度と、新たなデータに対する平均的な対数尤度の関係はどうなっているのでしょうか？

それを求めるために、

コインを50回投げる
その結果から $\theta$ と、結果に対する対数尤度を求める
新たにコインを50回投げて、求めた $\theta$ を使って対数尤度を求める作業を100回繰り返す。
100回の平均対数尤度を求める。
1~4を20回ほど繰り返す。

ということをしてみましょう。

青色がサンプルから求めた対数尤度(sample_lik)、赤色が新たな100回の試行から算出した平均対数尤度(mean_lik)です。

AIC

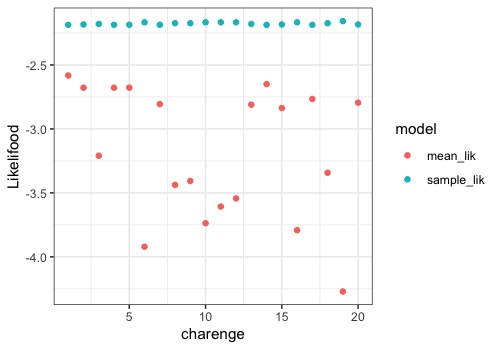
バラツキはありますが、どの試行においても青色の対数尤度が赤色よりも大きくなっているようです。（軸ラベルのスペルを間違えているのはご愛嬌、、）

このサンプルの対数尤度から平均対数尤度を引いてみると、その平均は約1になるため、サンプルの対数尤度は平均的に対数尤度1だけ大きく見積もっていることが分かります。

これは、得られたサンプルから $\theta$ を推定し、その $\theta$ を使ってサンプルの対数尤度を求めているので、 $\theta$ を二回使うことになり、バイアスがかかるために起こります。サンプルから求めた分散（標本分散）が母分散の推定値よりも小さくなることに似ています。このことから、サンプルから求められた対数尤度から1を引いた値が、新たなサンプルに対しての対数尤度の推定値としては良さげですね。

改めて見つめるAIC

さて、ここであらためてAICの式をみてみましょう。

$AIC= -2log(L(x | \theta ))+2p$

この式をよくみてみると、対数尤度 $log(L(x | \theta ))$ からパラメーター数pを引いたものに、-2をかけています。あれ....どこかで聞いたような...

$log(L(x | \theta ))$ は $\theta$ である時の変数xのもっともらしさ、二項分布の例ではサンプルから求めた対数尤度になります。また、二項分布のパラメーターは確率 $\theta$ のみですからパラメーター数は1です。

つまり、AICの式では、サンプルに対する対数尤度からパラメーター数を引くことで、新たなサンプルに対しての対数尤度の推定値を求めていたのです。このことからAICとは、

得られたデータに対してもっとも当てはまりの良いモデルを選択する基準ではなく、そのモデルを使って次のデータを当てはめた時に、平均的に当てはまりが良さそうなモデル、予測能力を最大化するためのモデルを選ぶ基準

であると言えそうです。

これがAICの正体です！サンプルにもっともよく当てはまるモデルを選ぶ基準がAICだと思っていると、それは違うよということですね。このAICがなぜこんな形になるのか、数学的導出について興味のある方は、こちらが分かりやすくまとまっているかと思います。(pdf注意)

https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/56989/1/yamaguchi.pdf

https://www.jstage.jst.go.jp/article/bjsiam/10/3/10_KJ00005768707/_pdf

まとめ

AICでのモデル選択が適切であるかどうかは議論がありますが、データの当てはまりの良さではなく、次にデーターを得た時に平均的に当てはまりが良いモデルを選択する基準であることは念頭に置いておきましょう。

特に因果推論などの変数選択に使う場合は、注意が必要ですね。

※本記事は筆者が個人的に学んだことをまとめた記事なります。数学の記法や詳細な理論、筆者の勘違い等で誤りがあった際はご指摘頂けると幸いです。

参考

今回はこちらの内容を参考にしました。統計モデリングを学ぶ方なら一度は目を通して頂きたい書籍です！

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)

作者:久保拓弥
岩波書店

Amazon

今回のRソースコード

library(tidyverse)

#確率を0.1~0.9まで変化させた時の対数尤度プロット
map_dbl(seq(0.1,0.9,0.1),~log(choose(50,40))+40*log(.)+10*log(01-.)) %>% 
  data_frame(Prob=seq(0.1,0.9,0.1),lik=.) %>% 
  ggplot(aes(x=Prob,y=lik))+
  geom_point()+
  geom_vline(xintercept = 0.8,col="red")+
  labs(y="Likelifood") 


# 確率が0.8場合に100回の試行結果に対する対数尤度のシミュレーション
lik_vec <- c()
set.seed(123)
for(i in 1:100){
  coin <- rbinom(50,1,0.5)
  omote <- sum(coin)
  lik <- log(choose(50,omote))+omote*log(0.8)+(50-omote)*log(0.2)
  lik_vec <- c(lik_vec,lik)
}

#ヒストグラム
data_frame(lik=lik_vec) %>% 
  ggplot(aes(x=lik))+
  theme_bw()+
  geom_histogram(bins = 10,fill="blue",alpha=0.5)+
  labs(x="Likelifood")

#サンプル対数尤度と新たなサンプル対数尤度平均を求める

sample_lik <- c()
mean_lik <- c()
set.seed(123)
for(i in 1:20){
  n <- 50
  coin <- rbinom(n,1,0.5)
  omote <- sum(coin)
  theta <- omote/n
  sample_lik <- c(sample_lik,log(choose(n,omote))+omote*log(theta)+(n-omote)*log(1-theta))
  
  l_vec <- c()
  for(j in 1:100){
    coin <- rbinom(n,1,0.5)
    omote <- sum(coin)
    l_vec <- c(l_vec,log(choose(n,omote))+omote*log(theta)+(n-omote)*log(1-theta))
  }
  mean_lik <- c(mean_lik,mean(l_vec))
}

#対数尤度の差の平均値
mean(sample_lik-mean_lik)

#グラフ化
data_frame(sample_lik = sample_lik,mean_lik = mean_lik) %>%
  gather(key="model",value=value) %>% 
  ggplot(aes(x=rep(1:20,2),y=value,col=model))+
  theme_bw()+
  geom_point()+
  labs(x="charenge",y="Likelifood")