リンゴで理解する分類問題~生成モデル、識別モデル、識別関数って何ですか？~

今回は、分類問題を学んでいてどうやら大きく分けて三つのアプローチがあるらしいと言うことで、その特徴を具体例を混じえてまとめてみます。

分類問題とは？

そもそも分類問題とは、例えば身長データから男女を分類するであったり、メールに書いてある単語から迷惑メールを分類するであったり、とにかく何かのデータを使って、それがどこに分類されるかを判断する問題になります！

よくわからないので具体的に

今回は以下のような分類問題を考えてみましょう！

あるリンゴ農家では、腐ったリンゴと正常なノーマルリンゴを分類するため、糖度を測ることにしました（見た目では分からないため）。糖度が高い方が腐っている確率が高いのは分かっていますが、基準がないので試しに200個のリンゴの糖度を測り、切って確かめてみました。このデータから糖度基準を作るにはどうしたら良いでしょうか？

この問題を3つのアプローチに触れながら考えてみましょう。ちなみに今回は全て教師あり学習です。

まずはグラフ化

とりあえず、データをグラフ化してみましょう。データは腐っていたら1 、ノーマルだったら0になっています。

f:id:h-wadsworth02:20181226223109p:plain

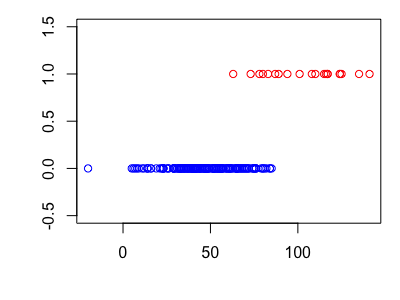
x軸が糖度を表していて、糖度が100を超えると多くのリンゴが腐っているみたいです。ちなみ今回は、1/10の確率でリンゴは腐っていると仮定して、以下のソースコードで作成しました。

>#1/10の確率でリンゴが腐っていると仮定（200個中20個腐っている）
> rot <- round(rnorm(20,100,20))
> normal <- round(rnorm(180,50,20))
> y <- rep(c(1,0) , c(20,180))
> apple_data <- data.frame("x" =c(rot,normal),
+                  "y" = y)
> head(apple_data)
    x y
1 108 1
2 117 1
3  78 1
4  73 1
5 116 1
6 141 1

分類問題の解き方

分類問題は、ある値だった時それがあるカテゴリーである確率求めることで解くことができます。つまり、糖度の値が $x$ だった場合に腐っている確率を求めることができれば、分類問題が解けそうです。

これは条件付き確率に等しいので、腐っている時を $C_{1}$ 、ノーマルな時を $C_{0}$ として、式で表すと

$\large p(C_{k}\,|\,x)$

となります。この確率を求めることが分類問題の肝になります！

その1：識別モデル

まず一つ目は識別モデルです。これはロジスティック回帰やニューラルネットなど、データ $x$ を入れるとそのまま条件付き確率を出してくれるアプローチになり、新たなデータに対しては閾値を設けることで分類することができます。実際にロジスティック回帰で解いてみましょう。

> (model <- glm(data=apple_data,y~x,family = binomial))

Call:  glm(formula = y ~ x, family = binomial, data = apple_data)

Coefficients:
(Intercept)            x  
   -16.1569       0.1899  

Degrees of Freedom: 199 Total (i.e. Null);  198 Residual
Null Deviance:      130 
Residual Deviance: 34.76   AIC: 38.76

このモデルを利用して、新たな $x$ が入力された時、腐っている確率が50%以上だったら1、未満だったら0とする関数を作成します。その時の腐っている確率も出力しておきましょう。

>library(e1071)
>library(dplyr)
>#xは入力データ、thetaは閾値
> rot_or <- function(x,theta){
+   prob <- sigmoid(model$coefficients[[1]]+model$coefficients[[2]]*x)*100 
+   print(paste(round(prob),"%"))
+   return(if_else(prob>=theta,1,0))
+ }
>#試しに実行
> rot_or(80,50)#糖度80の時
[1] "19 %"
[1] 0
> rot_or(100,50)#糖度100の時
[1] "74 %"
[1] 1

グラフ化（赤色は腐っている確率、青色はノーマルな確率を表す）

f:id:h-wadsworth02:20181226223649p:plain

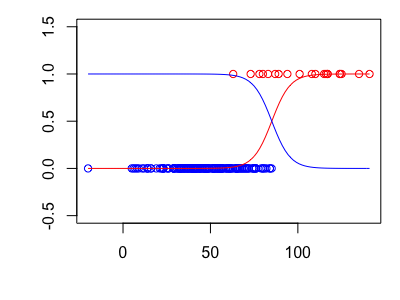
うまく分類できているようです！実行してお分かりの通り、識別モデルの分類には、訓練データからモデルを作成する推論段階とモデルの出力に従った決定段階に分けられます。

つまり、訓練データを使ってロジスティックモデルを作成したのが推論段階、モデルから閾値を設けて分類したのが決定段階になります。

その2：生成モデル

次は生成モデルです。分類問題は $p(C_{k}\,|\,x)$ を求めることが目的でした。これを事後確率と捉えてベイズ的に求めるのが生成モデルになります。ベイズの定理より、

$\large p(C_{k}\,|\,x) = \dfrac{p(x\,|\,C_{k})p(C_{k})}{p(x)}$

これを日本語で書くと、

$\small 糖度がxの時、リンゴが腐っている確率 = \\\ \small\dfrac{リンゴが腐っていた時、糖度がxになる確率\timesリンゴが腐っている確率}{糖度がxになる確率}$

となります。このモデルの場合 $p(C_{k}$ はサンプルの比率から求まります。しかし、 $p(x\,|\,C_{k})$ を求めるには、データが少ないと確率が0になってしまうので、たくさんの訓練データが必要になります。そこで、周辺農家にもお願いして、1万個のリンゴの糖度と腐っている個数を数えました。

>#今回も1/10の確率でリンゴが腐っていると仮定
> rot2 <- round(rnorm(1000,100,20))
> normal2 <- round(rnorm(9000,50,20))
> y2 <- rep(c(1,0) , c(1000,9000))
> apple_data2 <- data.frame("x" =c(rot2,normal2),
+                          "y" = y2)

このデータセットを使って、糖度が100の時に腐っている確率を求めてみます。

> #腐っている確率
> p_c1 <- 1000/10000
> #腐っているリンゴの中で、糖度が100である確率
> p_x_c1 <- nrow(filter(apple_data2, x ==100,y==1))/1000 
> #１万個のリンゴの中で、糖度が100である確率
> px <- nrow(filter(apple_data2,x==100))/10000
>> #糖度が100だった場合に腐っている確率
> (p_x_c1*p_c1)/px*100
[1] 73.68421

生成モデルを使って求めると約74%になり、先ほどのロジスティックの結果ともほぼ同じになっています！識別モデルと同じように50%を閾値として、関数にまとめてみます。

> rot_or2 <- function(x,theta){
+   #腐っている確率
+   p_c1 <- 100/10000
+   #腐っているリンゴの中で、糖度がxである確率
+   p_x_c1 <- function(suger){nrow(filter(apple_data2, x ==suger,y==1))/100} 
+   # #１万個のリンゴの中で、糖度がxである確率
+   px <- function(suger){nrow(filter(apple_data2,x==suger))/10000}
+   
+   prob <- ((p_x_c1(x)*p_c1)/px(x))*100 
+   print(paste(round(prob),"%"))
+   return(if_else(prob>=theta,1,0))
+ }
> rot_or2(80,50)
[1] "18 %"
[1] 0
> rot_or2(100,50)
[1] "74 %"
[1] 1

うまくいっているようです！この生成モデルの良いところは、腐っているリンゴの中で、糖度がxである確率分布が分かるため、新たな人工データの生成や外れ値検出にも応用できます。

その3：識別関数

最後は識別関数です。SVM（サポートベクターマシン）や決定木などが識別関数になります。この識別関数と上の二つの違いは、推論段階と決定段階を一気に行い、糖度がある一定値以上だったら腐っているとずばっ！と分けてしまいます。グラフで表すとこの緑の境界を求めるのが識別関数になります。
f:id:h-wadsworth02:20181226224405p:plain

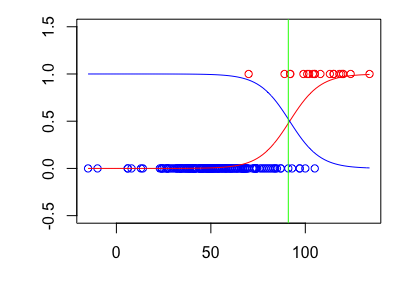
ちなみにこのラインは糖度が91のところなのですが、これは誤識別率（ノーマルなリンゴを腐っているor腐っているリンゴをノーマルであるとする割合）が最小の閾値でもあります。
この識別関数の求め方は色々あるので、今回は省略します。

このモデルの良いところは、訓練データが少なくても求めることができるということです。逆に確率として値が出ないため、閾値を設ける事が出来ない事がデメリットとしてあげられます。

まとめ

今回は、分類問題における三つのアプローチについてまとめてみました。どの手法を使うべきか、その目的に合わせて使い分けができるようになりたいですね。

最後までお読み頂きありがとうございました！

参考

ナイーブベイズ分類器を頑張って丁寧に解説してみる - Qiita

識別関数、識別モデル、生成モデルの違いを解説 - HELLO CYBERNETICS

パターン認識と機械学習上

作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
出版社/メーカー: 丸善出版
発売日: 2012/04/05
メディア: 単行本（ソフトカバー）
購入: 6人クリック: 33回
この商品を含むブログ (20件) を見る

今回のRソースコード

library(e1071)
library(dplyr)
library(magrittr)   
#データセットの作成
rot <- round(rnorm(20,100,20))
normal <- round(rnorm(180,50,20))
y <- rep(c(1,0) , c(20,180)) 
apple_data <- data.frame("x" =c(rot,normal),
                 "y" = y)   
#識別モデル
model <- glm(data=apple_data,y~x,family = binomial)   
rot_or <- function(x,theta){
  prob <- sigmoid(model$coefficients[[1]]+model$coefficients[[2]]*x)*100 
  print(paste(round(prob),"%"))
  return(if_else(prob>=theta,1,0))
}   
#生成モデル
#訓練データを増やす
rot2 <- round(rnorm(1000,100,20))
normal2 <- round(rnorm(9000,50,20))
y2 <- rep(c(1,0) , c(1000,9000))
apple_data2 <- data.frame("x" =c(rot2,normal2),
                         "y" = y2)  
rot_or2 <- function(x,theta){
  #腐っている確率
  p_c1 <- 100/10000
  #腐っているリンゴの中で、糖度がxである確率
  p_x_c1 <- function(suger){nrow(filter(apple_data2, x ==suger,y==1))/100} 
  #(すべてリンゴの中で)糖度がxである確率
  px <- function(suger){nrow(filter(apple_data2,x==suger))/10000}
  prob <- ((p_x_c1(x)*p_c1)/px(x))*100 
  print(paste(round(prob),"%"))
  return(if_else(prob>=theta,1,0))
}  
#識別関数
#識別モデルの結果を使用する
normprob <- function(x){sigmoid(-(model$coefficients[[1]]+model$coefficients[[2]]*x))}
rotptob <- function(x){sigmoid(model$coefficients[[1]]+model$coefficients[[2]]*x)}   
foo <- function(x){
  normprob(x)-rotptob(x)
}
ditin <- uniroot(foo,c(50,100))$root#二つのシグモイド関数の交点を求める   
#グラフ化
apple_data %$% {
  plot(x,y,col=rep(c("red","blue"),c(20,180))
       ,ylim = c(-0.5,1.5),xlab = "",ylab = "")
}
abline(v=distin,col = "green")
curve(rotptob,add = T,col = "red")
curve(normprob,add = T,col = "blue")