生存解析のすヽめ：カプランマイヤー法とコックス比例ハザードモデル

生存解析は医療の現場で用いられている手法で、ある薬を飲む群と飲まない群で死亡率が異なるのかなどといったアウトカムが生きるor死ぬなどの二値で、アウトカム発生までの時間の流れも考慮しなければならない場合に使用されます。

つまり、ビジネスの世界では、会員登録制サービスでの登録・解約に対する施策や、HR（ヒューマンリソース）分野での退職や転職に影響する要因などを検討する際にも用いることもできるでしょう。

今回は、そんな応用範囲が広いであろう生存解析について紹介していきます。生存解析は少し複雑ですので、詳細な理論等は参考サイト等をご参照ください。

生存解析の立ち位置
生存関数、ハザード関数、累積ハザード関数
カプランマイヤー法による解析
コックス比例ハザードモデル
Rで生存解析
まとめ
参考

生存解析の立ち位置

アウトカムが起こる or 起こらないなどの二値であるデータに対する解析法で、有名なものとしてはロジスティック回帰があります。ロジスティック回帰は、ある商品を買うかどうかなどの購買行動に対して, どんな要因が影響しているかなどの検討や、どれぐらいの確率で商品を購入するかなどの予測にも用いることが出来ます。生存解析でもアウトカムは二値ですが、ロジスティック回帰とは何が違うのでしょうか？

生存解析とロジスティック回帰の最も大きな違いは、アウトカムまでの時間の長さを考慮するかどうかにあります。例えば、会員制登録サービスの顧客が、解約するかどうかに影響する要因を検討したい場合、解約する人の中には、登録から解約まで数日の人もいれば、数週間、数ヶ月の人もいるでしょう。その登録している間の長さも考慮して解析出来るのが生存解析です。

生存解析の中でも有名な解析法が2つあり、一つはカプランマイヤー法(Kaplan-Meier)によるもの、もう一つはコックス比例ハザードモデルによるものです。

この2つの違いは、カプランマイヤー法が記述や単変量の比較を目的にするのに対して、コックス比例ハザードモデルは、多変量の要因解析を目的とすることです。

以上をまとめると生存解析の立ち位置とは以下のようになります。

アウトカムが二値で、アウトカム発生までの時間には興味がない：ロジスティック回帰
アウトカムが二値で、アウトカム発生までの時間も考慮したい：生存解析
- 検討したい要因は1つだけ：カプランマイヤー法
- 検討したい要因がたくさんある：コックス比例ハザードモデル

生存関数、ハザード関数、累積ハザード関数

具体的な手法の前に、そもそも生存解析とは何をするものなのかを説明しましょう。少しややこしいのでざっくりと理解できればOKです。生存解析とはズバリ"ハザード"をモデル化することを目的とした解析手法になります。ハザードとは、ある時点で生きていて、その次の時点で死亡する確率のことで、ハザードをモデル化したものをハザード関数：h(t)と呼びます。

例えば、10人の人を生まれてから死ぬまで毎年追跡するとしましょう。追跡開始5年後に1人が死亡しました。5年後に死亡する確率（ハザード）は1/10ですね。さらにその2年後に今度は2人死亡しました。この時9人が生存していて、そのうちの2人が死亡したので、ハザードは2/9となり、その2年後にも2人死亡したとするとハザードは2/7となります。このハザードをある関数でモデル化したとすると

$h(5) = \dfrac{1}{10}\\ h(7) = \dfrac{2}{9}\\ h(9) = \dfrac{2}{7}$

と表すことができます。また累積ハザード関数：H(t)とは、ある時点で死亡している確率を表し、先ほど同様に表すと

$H(5) = \dfrac{1}{10}\\ H(7) = \dfrac{3}{10}\\ H(9) = \dfrac{5}{10}$

となりますね。

今度は逆にある点で生きている確率を表す生存確率について考えてみます。5年後は9人が生きているので生存確率は9/10、その2年後のは7人が生きているので7/10、さらにその2年後は5人が生きているので5/10となります。この生存確率をモデル化したものを生存関数：S(t)と呼び、先ほどと同じように表してみると

$S(5) = \dfrac{9}{10}\\ S(7) = \dfrac{7}{10}\\ S(9) = \dfrac{5}{10}$

となります。1から累積ハザードを引くと生存確率となるため、累積ハザード関数から生存関数を求めることもできます。

ところで生存確率は

ある時点で生きている、かつ、その次の時点でも生きている確率

とも言い換えることができます。つまり、

$S(5) = p(0年目で生きている)\times p(5年目で生きてる)\\ =1\times\dfrac{9}{10}\\ =\dfrac{9}{10}\\ S(7) = p(5年目まで生きている)\times p(7年目で生きている)\\ = \dfrac{9}{10} \times \dfrac{7}{9}\\ = \dfrac{7}{10}\\ S(9) = p(7年目まで生きている)\times p(9年目で生きている)\\ = \dfrac{7}{10} \times \dfrac{5}{7}\\ = \dfrac{5}{10}$

とも表せます。ここで、ある時点で生きている確率は1からハザードを引いた確率に等しいので、ハザード関数から生存関数を求めることができます。

このように生存関数、ハザード関数、累積ハザード関数をどれも等価なものであるため、どれを求めても結局は同じになり数式上でも変換可能です。

長くなりましたが結局、

カプランマイヤー法：生存確率やハザードをモデル化せず、確率のまま解析するノンパラメトリックな解析法
コックス比例ハザードモデル：ハザードをモデル化することを目的としたセミパラメトリックな解析法

になるので、ターゲットが少し違うだけで意味合いは同じであることを覚えておきましょう。（なぜパラメトリックではなくセミパラメトリックなのかはまた後ほど）

補足：その他の生存解析法

生存解析にはその他いろいろな方法がありますが、大きく分類すると機械学習系と統計モデル系（〜系は筆者のオリジナルワードです）があり、さらに統計モデル系の中には、パラメトリックモデル、セミパラメトリックモデル、ノンパラメトリックモデルがあります。生存するかどうかの予測に興味があれば、機械学習系のモデルを使い、要因や因果関係に興味があれば統計モデル系を使います。

特に統計モデル系では、どの解析手法を使うかによって制約が異なるので、注意が必要です。例えば、本記事では紹介しないパラメトリックモデルの例では、生存関数を指数分布やワイブル分布でモデル化して解析を行いますが、分布を決め打ちしてしまっているため現実とはかけ離れる場合があります。

この辺りは深入りするとかなり複雑になるので、その他の手法にご興味がある方は、下記参考サイト様などをご覧ください。

カプランマイヤー法による解析

今回は肺ガンと死亡率に関する226人のデータを使って、男女によって肺がんによる死亡率に違いがあるかどうかを検討します。データは以下のような感じです。

inst	time	status	age	sex	ph.ecog	ph.karno	pat.karno	meal.cal	wt.loss
3	300	2	74	1	1	90	100	1175	NA
3	500	2	68	1	0	90	90	1225	15
3	1000	1	56	1	0	90	90	NA	15
5	200	2	57	1	1	90	60	1150	11
1	900	2	60	1	0	100	90	NA	0
12	1000	1	74	1	1	50	80	513	0

Instは所属機関、timeは死亡までに日数、statusは死亡(2)か打ち切り(1)か（後述します）、ageは年齢、sexは性別(男性1,女性 2)、ph.ecog、ph.karno、 pat.karnoは医学指標、mean.calは平均摂取カロリー、we lossは死亡前6か月間の体重減少量です。今回は簡単にするために、死亡までの日数を100日単位で丸めています。

ここで打ち切り(censor)とは、アウトカムが観測されるまえにデータが途切れてしまった場合のことを指します。例えば、明らかに肺がんに関係なく死亡した場合、転院となった場合、事情によりデータ収集ができなった場合などなど打ち切りの理由は様々ですが、これはアウトカムの発生とは区別する必要があります。

さて、それではカプランマイヤー法で解析を行なっていきます。カプランマイヤー法の目的は生存確率を求めて、その確率に差があるかどうかという観点で解析を行います。

まずは、アウトカム発生までの時間ごとの生存確率を計算していきましょう。とりあえず、0日目の性別ごとの人数と100日目までの死亡数を数えてみます。

0日の男女の人数

sex	n
m	138
w	90

100日目までの死亡数

sex	1	2
m	NA	24
w	1	7

死亡者が男性24人、女性7人、打ち切りが1人ですね。以上から生存確率を求めます。

$男性 : \dfrac{138-24}{138}= \dfrac{114}{138}\\ 女性：\dfrac{90-7}{90}=\dfrac{83}{90}$

となります。この段階では打ち切りは考慮されていません。続いて、101日目から200日目の死亡数は

sex	1	2
m	6	30
w	5	11

となって、100日目までに女性の打ち切りが1人いたことに注意して、200日目時点での生存確率は、100日目まで生きている確率と200日目まで生きている確率から求められるので、

$男性 : \dfrac{114}{138}\times\dfrac{114-30}{114} \\ 女性： \dfrac{83}{90}\times\dfrac{82-11}{82}$

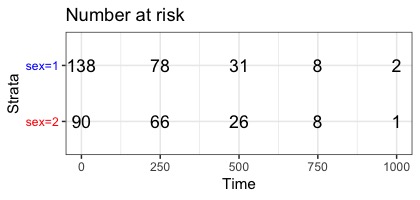
となります。ちなみに女性の82という人数は、前の時点での打ち切りを抜いた数になっています。つまり、101日目から200日目までで死亡する可能性が残っている、リスクにさらされている人数という意味でnumber at riskと言います。

さて、このように順番に生存確率を求めていくと

男性

time	n.risk	n.event	n.censor	surv
100	138	24	0	0.8260870
200	114	30	6	0.6086957
300	78	20	10	0.4526198
400	48	15	2	0.3111761
500	31	7	4	0.2409106
600	20	7	0	0.1565919
700	13	5	0	0.0963642
800	8	2	0	0.0722732
900	6	2	2	0.0481821
1100	2	0	2	0.0481821

女性

time	n.risk	n.event	n.censor	surv
100	90	7	1	0.9222222
200	82	11	5	0.7985095
300	66	9	14	0.6896218
400	43	10	7	0.5292447
500	26	5	0	0.4274668
600	21	3	7	0.3664001
700	11	3	0	0.2664728
800	8	5	1	0.0999273
900	2	0	1	0.0999273
1000	1	0	1	0.0999273

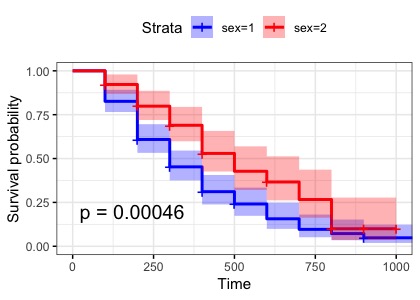
となります。この生存確率を95%信頼区間（グリーンウッド Greenwood の公式なるものを使って分散を求めます）とともにグラフにしてみると

生存解析

これをみると女性の方が生存確率が高そうですね。実はカプランマイヤー法は記述と単変量の比較が目的であるため、これで終わりなのです。これを統計的に検定するのが”生存確率に差はない”を帰無仮説としたログランク検定という方法で、グラフに表示されているp値がその結果です。手法の詳細は書きませんが、イメージとしては、

	死亡	生存
男性	24	114
女性	7	83

のような2×2のカイ二乗検定を各時点で合算した統計量を使って行います。詳細は参考（１）をご覧ください。

コックス比例ハザードモデル

カプランマイヤー法は、データの可視化や単純な比較などに使うことはできますが、検討したい要因がたくさんあった場合は対処できません。そこで、多くの変数を投入して解析できるのが、コックス比例ハザードモデルです。

コッス比例ハザードモデルは名前の通り、ハザードを

$h(t) = h_{0}(t) \exp(\beta_{1}x_{1} + \beta_{2}x_{2}+\beta_{3}x_{3}.....)$

とモデル化します。この式が表すのは、時間に依存する部分と依存しない部分に分けてt時点のハザードを求めています。

ここからが少しややこしいのですが、コックス比例ハザードモデルでは、ハザードの値を直接求めず、その比率で変数の影響力を解析するという妙技を使います。つまり、ハザードを直接モデル化はしませんが、要因がハザードにどれぐらい影響しているのかということは分かるのです。このことからセミパラメトリックモデルと呼ばれています。

例えば、変数は性別(1 or 2)のみだとして、先ほどのハザードの比率を求めてみると

$\dfrac{h_{0}(t) \exp(\beta_{1}\times 2)}{h_{0}(t) \exp(\beta_{1}\times 1)}\\ =exp(\beta_{1})$

となって、うまい具合にh(t)が約分されるので、性別の係数のみが残ります。これはt時点のハザードは性別が男性(1)の場合に比べて、女性の場合は $exp(\beta_{1})$ 倍になるという意味になります。この係数を実際に求めてみると

$\beta_{1} = -0.56$

$\exp(\beta_{1}) = 0.56$

となるので、t時点の女性のハザードは男性に比べて0.56倍、つまり半分ぐらいになるということです。この係数の求め方は部分尤度法というややこしい方法を使うのですが、今回は説明を省かせて頂きます。

ところで、なぜこんなことをするかというと、ハザードを直接モデル化するには、ハザードを何らかの関数で表すことができるという仮定を置かなければなりません。しかし、実際にはどんな関数になるのかは誰にもわからないので、諦めてそのハザードの比率から要因を検討しようというのがコックス比例ハザードモデルの考えです。

それでは変数を色々入れて、係数を求めてみると

	exp(coef)	lower .95	upper .95
sex	0.5554815	0.3741708	0.8246491
age	1.0099655	0.9873982	1.0330487
ph.ecog	2.0118597	1.3005582	3.1121862
ph.karno	1.0202035	0.9978993	1.0430062
pat.karno	0.9890568	0.9738774	1.0044729
meal.cal	1.0000636	0.9995594	1.0005682
wt.loss	0.9854940	0.9706653	1.0005492

となって、性別とph.ecogという変数が、ハザード比で1を跨いでいないので影響を及ぼしていることが分かりますね。

ここで、お気付きの方もいらっしゃるかもしれませんが、このモデルではかなり強い制約を置いています。それは、ハザードの比が時間に関係なく一定であるという過程です。つまり、性別によるハザード比がt=100日目もt=500日目も同じであるということです。何とも強い仮定ですね。

本来であればこのあと、比例ハザード性の確認など色々と検討事項があるのですが、今回はざっくり概要編ということで省かせて頂きます。

Rで生存解析

Rで生存解析を行うにはsurvivalパッケージを使います。また、可視化にはsurvminerパッケージを使うと良いでしょう。

library(tidyverse)
library(survival)
library(survminer)

#データセットの読み込み
data(lung)

#100日単位で丸める
lung <- lung %>% 
  mutate(time = ceiling(time*0.01)*100)

ここからSurv{survival}とsurvfit{survival}を使ってカプランマイヤー法による解析を行います。

surv <- Surv(lung$time, lung$status)
fit <- survfit(surv ~ sex, data = lung)

> fit
Call: survfit(formula = surv ~ sex, data = lung)

        n events median 0.95LCL 0.95UCL
sex=1 138    112    300     300     400
sex=2  90     53    500     400     700


#図示

ggsurvplot(fit,
          pval = TRUE, #ログランク検定の結果
          conf.int = TRUE,#信頼区間の表示
          risk.table = TRUE, # 時点のnumber at riskの数を一緒に図示できる
          ggtheme = theme_bw(), # テーマを変えることもできる。
          palette = c(4, 2)　#色の指定
          )

結果の詳細を見るには通常のsummary{base}を使っても良いですが、surv_summary{survival}を使うとより見やすい形で結果を見ることができます。

また、可視化にはsurvfit{survival}の結果をplot{base}に渡しても図示してくれますが、ggsurvplot{survminer}を使うとより綺麗にグラフ化できます。

生存解析

ログランク検定はsurvdiff{survival}を使って実行できます。

> survdiff(Surv(time, status) ~ sex, data = lung)
Call:
survdiff(formula = Surv(time, status) ~ sex, data = lung)

        N Observed Expected (O-E)^2/E (O-E)^2/V
sex=1 138      112     92.2      4.23      12.3
sex=2  90       53     72.8      5.36      12.3

 Chisq= 12.3  on 1 degrees of freedom, p= 5e-04

さて次はコックス比例ハザードモデルです。coxph{survival}を使って実行します。

fit_cox <- coxph(Surv(time, status) ~ sex+age+ph.ecog+ph.karno+pat.karno+meal.cal+wt.loss , data =  lung)

> fit_cox
Call:
coxph(formula = Surv(time, status) ~ sex + age + ph.ecog + ph.karno + 
    pat.karno + meal.cal + wt.loss, data = lung)

                coef  exp(coef)   se(coef)      z       p
sex       -5.879e-01  5.555e-01  2.016e-01 -2.916 0.00354
age        9.916e-03  1.010e+00  1.153e-02  0.860 0.38976
ph.ecog    6.991e-01  2.012e+00  2.226e-01  3.141 0.00169
ph.karno   2.000e-02  1.020e+00  1.128e-02  1.774 0.07614
pat.karno -1.100e-02  9.891e-01  7.891e-03 -1.394 0.16319
meal.cal   6.364e-05  1.000e+00  2.573e-04  0.247 0.80468
wt.loss   -1.461e-02  9.855e-01  7.736e-03 -1.889 0.05889

Likelihood ratio test=27.63  on 7 df, p=0.0002561
n= 168, number of events= 121 
   (60 observations deleted due to missingness)

記事の中では触れていませんが、cox.zph{survival}を使うと比例ハザード性の検定ができます。帰無仮説は"比例ハザード性がある"ですので、棄却された場合はこのモデルの仮定が正しくない可能性があります。

cox.zph(fit_cox)
             rho   chisq      p
sex       0.1324  2.1025 0.1471
age       0.1247  2.0033 0.1570
ph.ecog   0.0387  0.1918 0.6614
ph.karno  0.2095  4.0585 0.0439
pat.karno 0.0247  0.0876 0.7672
meal.cal  0.2028  5.7240 0.0167
wt.loss   0.0506  0.4292 0.5124
GLOBAL        NA 15.1298 0.0344 #これはよく分かりません..