
引用元https://github.com/interpretml/DiCE
近年では、ブラックボックスと呼ばれる機械学習の解釈性に注目が集まっており、予測の結果について説明するための手法がいくつか考案されてます。代表的なものとしては、LIME(Local Surrogate)やSHAP(SHapley Additive exPlanation Values)があります。
例えば、ある病気になるかどうかの予測モデルを考えてみましょう。病気は、年齢や、性別、BMI、運動、食事習慣などから予測されます。
太郎さんがその病気にかかる確率が高いと予測されたとします。太郎さんがなぜ病気になりやすいと予測されたのかという疑問には、LIMEやSHAPが使えます。
一方で、どうすれば病気になりにくいか(病気となる確率が低いと予測されるのか)を知りたい場面もあるでしょう。
今回は、そんな疑問にお答えすべく、Microsoftが開発した反実仮想の生成手法、DiCEをご紹介します。
理想的な反実仮想の条件
予測値を低くする変数は、変数の値をいろいろ変化させれば見つかるかもしれません。
しかし、闇雲に変数を調整してもうまくいきません。 なぜなら、何この変数をどれぐらい変化させれば良いか、の組み合わせは膨大になりますし、年齢や性別のように変化させることがほぼ不可能な変数もあるからです。
ここで、理想的な反実仮想の条件を考えてみます。
- 条件1. 反実仮想は、現状の状態と似ている
- 条件2. 変化する変数が少ない
- 条件3. 変数の変化が現実的である
- (条件4. 反実仮想が多様である)
条件1、条件2は、変化する変数の数と幅が少ないことを意味します。予測確率を低くするために、体重を20kg落として、毎日2時間ジム行って、毎日500gの野菜を食べて、、、と現状からあまりに離れているのは、良い反実仮想とは言えません。反実仮想生成の目的は、最小限の変化で、最大限に目標とする予測値に近づけることです。
条件3は、現実的ではない変数変化が起きないようにするという意味です。体重を100kg減らすや、年齢を-10歳にするなどの変化は現実では不可能です。
条件4は、必須というわけではないですが、上記3つの条件を満たす反実仮想が複数あったときに、反実仮想は多様である方が意思決定しやすいということです。
食事を変えるのか、運動をするのか、はたまた減量をするのか、人によって実行しやすさが異なるため、色々提案してくれた方が良いということですね。
DiCE(Diverse Counterfactual Explanations)とは?
上記の制約を条件に変数を色々変化させれば、理想的な反実仮想を探し出すことができそうです。
アルゴリズムはいくつかありますが、一番シンプルなものは次のようなアルゴリズムです。
- y:達成したい値(病気になる確率など)
- x:元々のデータ
- c:反実仮想のデータ
- f(c):反実仮想データをもとにした予測値
式はいかついですが、
達成したい値yと反実仮想の予測値f(c)の誤差を小さくしろ
ただし、反実仮想cを、元々の状態xとあまり離すな
という意味の式です。
上記の思想を応用し、多様な反実仮想を生成することを得意とするのがDiCEです。
DiCEの詳細なアルゴリズムについては、こちらを
[1905.07697] Explaining Machine Learning Classifiers through Diverse Counterfactual Explanations
DiCEで反実仮想を生成
DiCEはpipで簡単にインストールできます。
pip install dice-ml
はじめに予測モデルを作ります。予測タスクは、bostonデータセットを使って、住宅価格が中央値より高くなるかどうかの2値予測です。低価格住宅(0)、高価格住宅(1)とでもしましょう。
モデルは、tensorflowとpytorch、scikit-learnに対応していますが、今回はお手軽にscikit-learnを使います。
import numpy as np import pandas as pd from sklearn.datasets import load_boston from sklearn.linear_model import LogisticRegression, LinearRegression from sklearn.model_selection import train_test_split import dice_ml boston = load_boston() x = pd.DataFrame(boston.data, columns=boston.feature_names) # 価格が中央値より高ければ1、そうでなければ0 y_bin = pd.Series([1 if x > np.median(boston.target) else 0 for x in boston.target]).rename("price")
変数は以下の通りです。
- CRIM:人口 1 人当たりの犯罪発生数
- ZN :25,000 平方フィート以上の住居区画の占める割合
- INDUS:小売業以外の商業が占める面積の割合
- CHAS:チャールズ川によるダミー変数 (1: 川の周辺, 0: それ以外)
- NOX:NOx の濃度
- RM:住居の平均部屋数
- AGE:1940 年より前に建てられた物件の割合
- DIS:5 つのボストン市の雇用施設からの距離 (重み付け済)
- RAD:環状高速道路へのアクセスしやすさ
- TAX:$10,000 ドルあたりの不動産税率の総計
- PTRATIO:町毎の児童と教師の比率
- B:町毎の黒人 (Bk) の比率を次の式で表したもの。 1000(Bk – 0.63)2
- LSTAT:給与の低い職業に従事する人口の割合 (%)
引用元:scikit-learn に付属しているデータセット – Python でデータサイエンス
x.head()
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00632 | 18 | 2.31 | 0 | 0.538 | 6.575 | 65.2 | 4.09 | 1 | 296 | 15.3 | 396.9 | 4.98 |
| 0.02731 | 0 | 7.07 | 0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2 | 242 | 17.8 | 396.9 | 9.14 |
| 0.02729 | 0 | 7.07 | 0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2 | 242 | 17.8 | 392.83 | 4.03 |
| 0.03237 | 0 | 2.18 | 0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3 | 222 | 18.7 | 394.63 | 2.94 |
| 0.06905 | 0 | 2.18 | 0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3 | 222 | 18.7 | 396.9 | 5.33 |
# テストデータ、訓練データに分ける。 train_x, test_x, train_y_bin, test_y_bin = train_test_split(x, y_bin, test_size=0.2, random_state=123) # モデル学習 model_logi = LogisticRegression() model_logi.fit(train_x, train_y_bin)
それでは、DiCEを使って反実仮想を生成してみましょう。
d = dice_ml.Data(dataframe = pd.concat([test_x, test_y], axis=1),# データは、変数とアウトカムの両方が必要 continuous_features = list(train_x.drop("CHAS", axis=1).columns), # 連続変数の指定 outcome_name = "price") m = dice_ml.Model(model=model_logi, backend="sklearn") exp = dice_ml.Dice(d, m)
dice_ml.Dataでは、反実仮想生成の元となるデータを作成します。変数とアウトカムが一つになっていることに注意してください。カテゴリ変数と連続変数は扱いが違うため、continuous_featuresで連続変数がどれかを指定します。
dice_ml.Modeでは、作成したモデルを渡します。今回はscikit-learnなので、backend=sklearnとします。
最後にdice_ml.Dice(d, m)として、準備完了です。早速反実仮想生成をしてみます。
from numpy.random import seed seed(123) pre_counter = test_x.iloc[0:2, :] dice_exp = exp.generate_counterfactuals(pre_counter, # 反実仮想を生成したいもとデータ total_CFs=3, # 反実仮想の数 desired_class = "opposite", # 目的とするクラスは反対方向へ、0、1などのクラスラベルでも良い ) dice_exp.visualize_as_dataframe(show_only_changes=True)# show_onlyで変数変化の差分のみを表示

テストデータ2サンプルで、それぞれ3つの反実仮想データを作成しました。1つ目は、高価格住宅になるための、2つ目は低価格住宅になるための反実仮想です。
高価格住宅になるには、部屋の数を増やしたり(RM)、税金を安くしたり(TAX)、低所得者の居住割合を減らしたり(LSTAT)することで、効果価格住宅(と予測される)になることがわかりますね。
逆に低価格住宅になるには、犯罪率が増えたり(CRIM)、雇用施設からの距離が遠くなる(DIS)ことが条件のようです。
また、generate_counterfactualsには、features_to_varyで、変化を許す変数を指定することができたり、permitted_rangeで変数の変化幅を制御できます。
dice_exp = exp.generate_counterfactuals(pre_counter,
total_CFs=3,
desired_class = "opposite",
features_to_vary=["RM", "AGE", "RAD", "LSTAT"], #変化を許す変数,
permitted_range = {"RM":[1, 10]},
)
dice_exp.visualize_as_dataframe(show_only_changes=True)
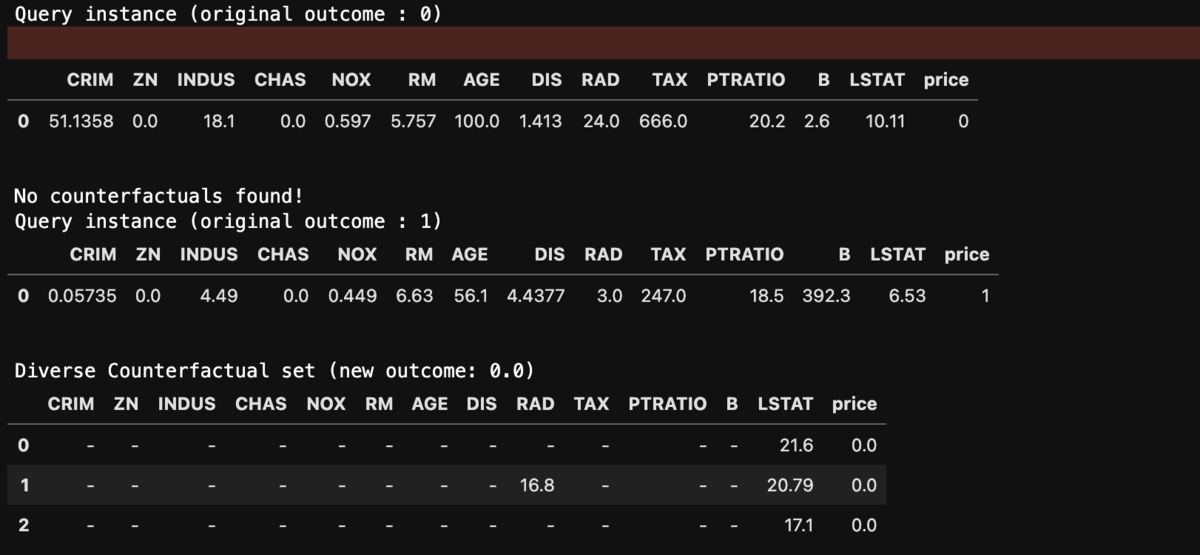
どうやら上記の条件でサンプル1が高価格物件になる条件は探せなかったようです。
逆に、低価格物件になる条件は指定した制約を満たしています。 ``
連続量予測の反実仮想
DiCEはRegressionモデルを使った連続量予測にも使うことができます。連続量の場合は、model_type="regressor"として、達成したい予測値のレンジを指定します。
# 回帰モデル # テストデータ、訓練データに分ける。 y = pd.Series(boston.target).rename("price") train_x, test_x, train_y, test_y = train_test_split(x, y, test_size=0.2, random_state=123) model_reg = LinearRegression() model_reg.fit(train_x, train_y)
d = dice_ml.Data(dataframe=pd.concat([test_x, test_y], axis=1), continuous_features=list(boston.feature_names), outcome_name="price") m = dice_ml.Model(model=model_reg, backend="sklearn", model_type="regressor") exp = dice_ml.Dice(d, m) pre_counter = test_x.iloc[0:1, :] dice_exp = exp.generate_counterfactuals(pre_counter, total_CFs=3, desired_range=[30,100]) dice_exp.visualize_as_dataframe(show_only_changes=True)
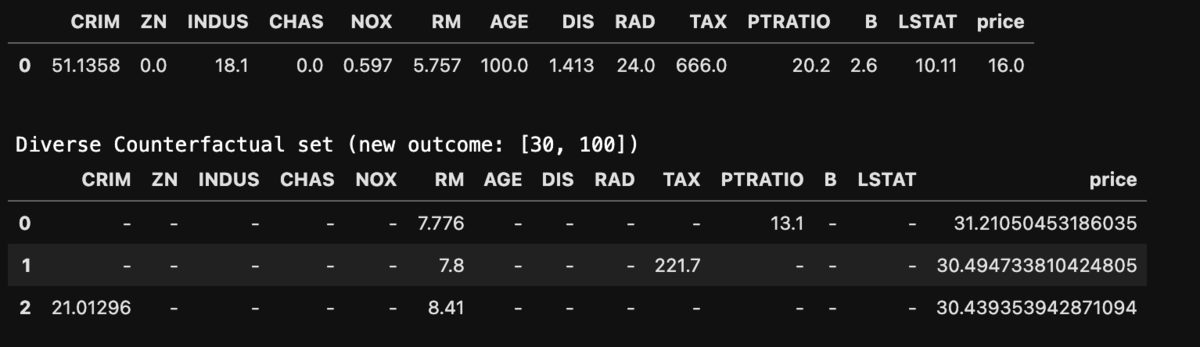
まとめ
機械学習モデルの解釈性が必要とされる場面では、DiCEの情報は重宝しそうです。また、変数の変化と予測値の関係性が期待通りになっているかの確認にも使えますね。