今回は、Rのstanを使ってベイズ推定を使った単回帰分析を行なっていきます。 本来であればベイズ推定を使わなくても単回帰分析のパラメーターは推定できるのですが、stanに慣れるためにもまずは簡単なところからですね。
最後には通常の単回帰分析と結果の比較も行います。 前回の二項分布パラメーター推定では扱わなかったstanの新たな機能にも触れていきますよー
stanを使わない方向けにもベイズ推定の流れをまとめます!
通常の単回帰分析
今回のデータは生徒100人の一日の勉強時間とテスト点数の仮想データとしましょう。
>library(ggplot2) > study <- sample(seq(1,10),replace = T,100) > Y <- 10+ 7*study+round(rnorm(100,0,5)) > st_score <- data.frame(Y,study) > head(st_score) Y study 1 62 7 2 51 6 3 70 9 4 69 8 5 33 4 6 35 4 >#グラフ化 > st_score %>% + ggplot(aes(study,Y))+ + geom_point()
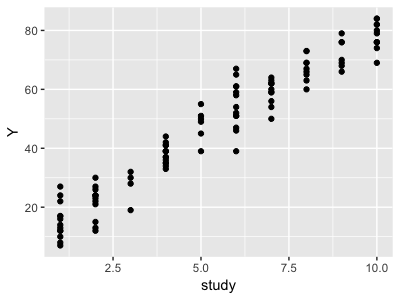
目的変数Yがテストの点数です。このデータに通常の回帰分析を行います。
> st_score %>% lm(Y~study,data=.) -> lm_model > summary( lm_model) Call: lm(formula = Y ~ study, data = .) Residuals: Min 1Q Median 3Q Max -12.9016 -3.6370 0.0662 3.3498 15.0984 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 8.7788 1.1485 7.644 1.45e-11 *** study 7.1871 0.1883 38.174 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 5.517 on 98 degrees of freedom Multiple R-squared: 0.937, Adjusted R-squared: 0.9363 F-statistic: 1457 on 1 and 98 DF, p-value: < 2.2e-16
という結果になりました。1日の勉強時間が1時間増えるとテストの点数が7.2点上昇するようです。
先ほどのグラフに回帰直線の95%信頼区間と予測値の信頼区間を書いてみます。
study_new <- data.frame(study = seq(1,10)) coef95 <- predict(lm_model,study_new ,interval = "confidence") pred95 <- predict(lm_model,study_new,interval = "prediction") st_score %>% ggplot()+ geom_point(aes(study,Y))+ geom_line(data = data.frame(study_new,coef95), aes(x=study,y=fit),color="black",linetype = 1,size = 0.5)+ geom_ribbon(data = data.frame(study_new,coef95), aes(x=study,ymin=lwr,ymax=upr),fill = "blue",alpha=0.5)+ geom_line(data = data.frame(study_new,pred95), aes(x=study,y=lwr),color="black",linetype = 2)+ geom_line(data = data.frame(study_new,pred95), aes(x=study,y=upr),color="black",linetype = 2)+ title("lm_model")

青色が回帰直線の信頼区間、破線が予測値の信頼区間を表しています。ここまでは普通の単回帰分析ですね。
ベイズ推定で単回帰分析
何をするか
さて、stanを使ってベイズ推定を行う前に、ベイズ推定の流れを説明しておきます。
ベイズ推定では以下のように単回帰分析を行います。
①すでに分かっている点数(Y)と勉強時間(study)から、ベイズ推定を用いて回帰直線パラメーターの確率分布 を求める。
←回帰直線パラメーターの確率分布
②①の確率分布を使って、予測値の確率分布を平均、標準偏差
に従う正規分布として求める。
←予測値の確率分布
を求める。
以上がベイズ推定の流れになります。
どうやるか
それでは、ざっくりと大枠を掴んだところで、さっそくRとstanを使ってモデリングしていきます。
まず①ですが、右辺の分母は定数と扱えるので
としておきます。
するとはパラメーターが
だった場合に
となる確率を表すので尤度関数になります。
ここで、
とすると、点数は、平均
、標準偏差
の正規分布に従うので
と表すことができます。この正規分布から得られる確率密度の1からnまでの掛け合わせが尤度となるので、先ほどの尤度関数は
となります。
また、はパラメーターの事前分布ですが、今回は何も情報がないので無情報分布としておきましょう。すると結局
をモデリングすることになります。
これで①の準備が整いました。stanでモデリングしてみます。
data { int<lower=0> N;//生徒数 real Y[N];//点数 real study[N];//勉強時間 } parameters { real a; real b; real <lower = 0>sigma; } //data,parametersの値から新たにサンプリングする transformed parameters{ real mu[N]; for(n in 1:N){ mu[n] = a+b*study[n]; } } model { for (n in 1:N){ Y[n]~normal(mu[n],sigma); } }
transformed parameteresはdataやparametersで定義されている値を使って新たにサンプリングを行います。今回は、サンプリングされたa,bとデータstudyを使って回帰直線muをサンプリングしています。
また、for文での繰り返し処理が尤度関数×事前分布の掛け合わせ(厳密には内部で対数尤度を足している)を行っています。
本来であれば、事前分布の分布も定義する必要がありますが、stanではパラメーターの分布を何も指定しなければ、勝手に無情報分布を選んでくれます。
ここまでで①ができました。続いて②をモデリングしていきましょう。
②ではRの
study_new <- data.frame(study = seq(1,10)) coef95 <- predict(lm_model,study_new ,interval = "confidence") pred95 <- predict(lm_model,study_new,interval = "prediction")
に相当することを行なっていきます。
まず、先ほどモデリングされたパラメーターを使って回帰直線の予測値とscoreの予測値
を以下のようにします。
これをモデリングするためにstanファイルに以下を書き加えます。
data { int<lower=0> N; real Y[N]; real study[N]; int N_new; real study_new[N_new];//予測値を出したい範囲 } generated quantities{ real mu_new[N_new]; real y_new[N_new]; for(n in 1:N_new){ mu_new[n] = a+b*study_new[n]; y_new[n] = normal_rng(mu_new[n],sigma); } }
まず、最初のdataにstudy_newを渡すための変数を加えます。そして、新たに登場したgenerated quantitiesは、サンプリング後のパラメーターを使って新たな値を作成します。
このgenerated quantitiesはtransformed parameteresと違って、全てのサンプリングが終了した後に実行されます。そのため、stanファイルに書かなくても後から作成することができるのですが、こちらで定義しておいた方がスムーズに結果を出すことができるでしょう。
さてこれで準備が整いました。最終的なstanコードは以下になります。
data { int<lower=0> N;//生徒数 real Y[N];//点数 real study[N];//勉強時間 int N_new; real study_new[N_new];//予測値を出したい範囲 } parameters { real a; real b; real <lower = 0>sigma; } //data,parametersの値から新たにサンプリングする transformed parameters{ real mu[N]; for(n in 1:N){ mu[n] = a+b*study[n]; } } model { for (n in 1:N){ Y[n]~normal(mu[n],sigma); } } generated quantities{ real mu_new[N_new]; real y_new[N_new]; for(n in 1:N_new){ mu_new[n] = a+b*study_new[n]; y_new[n] = normal_rng(mu_new[n],sigma); } }
stanは上から順に実行されるので記述の順番に気をつけてください。 このstanファイルをregression.stanとして保存します。
Rのスクリプトファイルに戻って、stanを実行しましょう!
#stanファルの読み込み stanmodel <- stan_model("regression.stan") #データをリスト型で格納 data = list(N= nrow(st_score),study=st_score$study,Y= st_score$Y, N_new = nrow(study_new),study_new = study_new$study) #データを渡してサンプリング stan_fit_res <- sampling(stanmodel,data = data) #結果の取り出し stan_fit <- rstan::extract(stan_fit_res)
さてこれでベイズ推定が完了しました。
まずは、回帰直線の切片と傾きを通常の回帰分析と比べてみましょう。
#通常の回帰分析で求めた切片と傾きの区間推定値 > lm_model Call: lm(formula = Y ~ study, data = .) Coefficients: (Intercept) study 8.779 7.187 > confint(lm_model) 2.5 % 97.5 % (Intercept) 6.499757 11.057926 study 6.813512 7.560753 #ベイズ推定した切片の平均値、2.5%、97.5%タイル値 > mean(stan_fit$a) [1] 8.819646 > quantile(stan_fit$a,prob=c(0.025,0.975)) 2.5% 97.5% 6.534484 11.138849 ベイズ推定した傾きの平均値、2.5%、97.5%タイル値 > mean(stan_fit$b) [1] 7.182167 > quantile(stan_fit$b,prob=c(0.025,0.975)) 2.5% 97.5% 6.810002 7.551476
ほぼ同じ結果になっていますね。
続いて回帰直線の95%信頼区間、予測値の95%信頼区間をグラフにしてみましょう。まずは扱いやすいようにデータフレームに加工します。
> #それぞれの勉強時間ごとのタイル値を求める > apply(stan_fit$mu_new,2,quantile,probs=c(0.025, 0.975)) %>% #転置してデータフレームに整形する t() %>% data.frame(study_new,.) ->mu_new_df > colnames(mu_new_df) <- c("study","25%","97.5%") >#回帰直線の信頼区間 > quantile_df study 25% 97.5% 1 1 14.03855 18.01428 2 2 21.51581 24.87054 3 3 28.94716 31.76470 4 4 36.36693 38.73402 5 5 43.66429 45.78955 6 6 50.83837 52.98826 7 7 57.87362 60.30258 8 8 64.80373 67.72861 9 9 71.71571 75.17867 10 10 78.55824 82.66124 >#予測値の信頼区間 > apply(stan_fit$y_new,2,quantile,probs=c(0.025, 0.975)) %>% t() %>% data.frame(study_new,.) -> y_new_df > colnames(y_new_df) <- c("study","25%","97.5%") > y_new_df study 25% 97.5% 1 1 5.092725 27.31094 2 2 11.736867 34.61137 3 3 19.428660 41.37392 4 4 26.871123 48.66943 5 5 33.600933 55.43119 6 6 40.310366 62.76549 7 7 47.865658 70.16330 8 8 55.175584 77.64518 9 9 62.353089 84.44464 10 10 69.318226 91.85203
これを先ほどと同じようにグラフ化します。
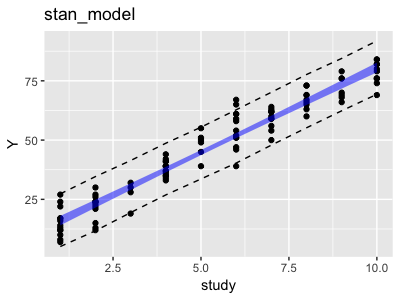
どこかでみたようなグラフですね。これはパラメーターの事前分布に無情報分布を選んだため、通常の最尤法で求めた結果とほぼ同じになります。
まとめ
今回はベイズ推定で単回帰分析行い、その結果を通常の単回帰分析と比較しました。
ベイズ推定では、事前分布に無情報分布を選ぶと通常の最尤法と同じ結果になります。
前回も書いたようにベイズ推定の良いところは、さらに複雑なモデリングができるところにあります。
stanにもだいぶ慣れてきたので、次回からは複雑なモデリングにも挑戦していきます!
※本記事は筆者が個人的に学んだことをまとめた記事なります。数学の記法や詳細な理論等で誤りがあった際はご指摘頂けると幸いです。
参考
こちらの内容をアレンジして記事を書きました。これほどわかりやすくベイズモデリングを学べる書籍はほとんどないでしょう。

StanとRでベイズ統計モデリング (Wonderful R)
- 作者: 松浦健太郎,石田基広
- 出版社/メーカー: 共立出版
- 発売日: 2016/10/25
- メディア: 単行本
- この商品を含むブログ (10件) を見る
いつもお世話になっているブログ 前半にベイズ推定の流れが書いてあります。