前回の続きで、今回は主に連続型確率分布である正規分布、t分布を扱っていきます。ここまで理解できれば、統計が楽しくなるはずです!正規分布からt分布の導出までを出来るだけ式を使わずにまとめていきます!
正規分布
まずは、一番有名な確率分布といっても過言ではない正規分布からいきましょう!どのようなものがこの分布に従うかというと、、、、それはそれは答えられないほど多くの事象がこの正規分布に従います。
今回は、長さ10cmの棒を作る機械を考えてみましょう(なんじゃそりゃ、、、)。この機械の精度を調べるために、出来上がった棒の長さを測り、それを記録することを10万回ぐらい繰り返しました。
すると以下のようなヒストグラムになります。
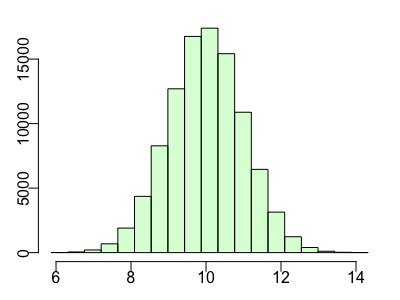
10cmの長さになる棒が一番多いですが、長くなったり、短くなったりする棒もあります。この平均値を中心に左右対称に広がっている分布が正規分布です。
この時、およそ10cmになる棒が一番多いのは確かですが、長さを精密に測ると10.023cmだったり、9.99993cmだったりになるはずです。ヒストグラムの幅をだんだんと狭くしてみると....
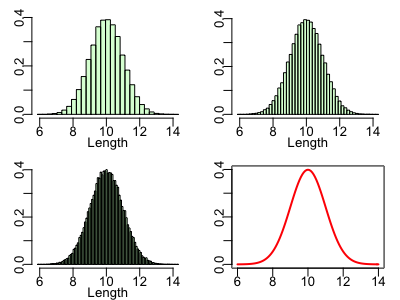
この分布は連続確率分布となり、平均約10cm、標準偏差1cmの正規分布になります。
正規分布は平均と標準偏差
が決まると分布の形が決まって、式で表すと
となります。難しい場合は、とりあえずこんなゴツイ式なのかというぐらいでOKです。
前回も書いた通り、連続確率分布の場合は縦軸が確率ではなく、相対的な起こりやすさを表していることに注意してください。

脱統計初学者!確率分布まとめ~ベルヌーイ分布・二項分布・ポワソン分布・指数分布~ - 医療職からデータサイエンティストへ
今度は、機械で生成された100本の棒の平均値を計算して、記録する作業を1万回ぐらい繰り返してみましょう。すると
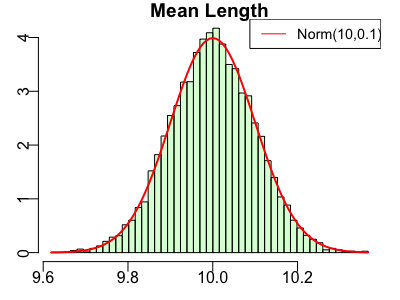
この平均値の分布も正規分布になります!この分布は平均約10cm、標準偏差0.1cmの正規分布で近似することができます。(赤線)
ここで、重要な正規分布の特徴が出てきました。サンプリングした平均値の分散は、元々の分散/サンプル数となります。
今回もともとの分散が1cmだったため、100個サンプルした平均値の分散は1/100(標準偏差は1/10)になってます。
さて、この分布がわかると何が嬉しいかというと、次に100本の平均値を測った時、この分布から大きく外れているようであれば、この機械が壊れている可能性があると判断することができます。
例えば以下の図のように、100個の平均値が9.8cmより小さい、もしくは、10.2cmより大きくなり、近似した正規分布の95%に入っていなければ、故障の疑いがありそうです。
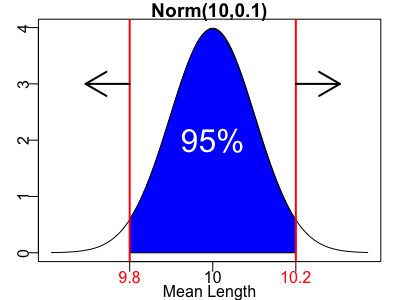
ちなみに9.8cm、10.2cmは、プラスマイナス2倍の標準偏差の間が約95%になることを利用して、近似的に求めることも可能です。
z値
ここで、一つ問題があります。100個の平均値を計算すれば、10cmの棒を作る機械の検査ができますが、設定を5cmにした場合や50個の平均値しか検査できない場合は、分布が分からないため検査することができません。
この問題を解決するために、平均の値が平均0、分散1の正規分布に従うように基準化したZ値というものを使います。
Z値は以下のように計算されます。
この式の意味をグラフィカルにみてみましょう。
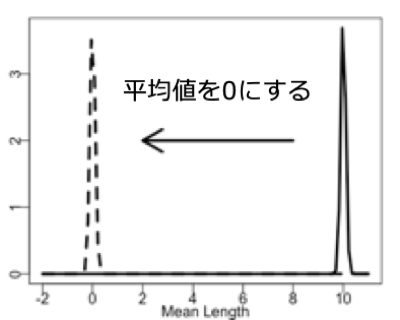
まず、分子ではサンプルの平均値から母集団の平均値
を引くことで、サンプルした平均値の中心を0にします。
そして、平均値分布の標準偏差(元々の分散/サンプル数の平方根)で割ることで分散を1にしています。
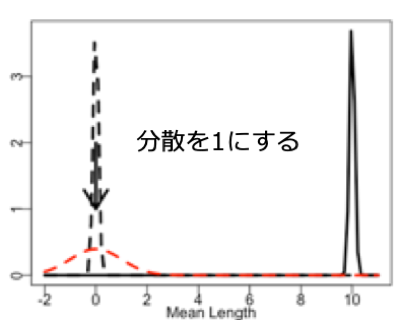
このZ値が従う分布を標準正規分布と呼び、これであればどんな場合でも故障を検査することができます。
例えば機械の設定を5cmに変えて、50個抜き出した時の平均値が4.8cmだった時、この機械は故障していると言えるでしょうか?
まずはz値を求めてみましょう。
先ほどの標準正規分布で見てみると、
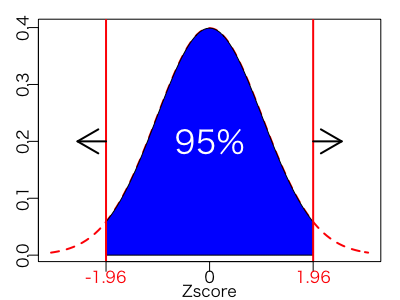
Z値-1.98~1.98の間に95%のデータが入っているので、Z値-1.4は故障ではなく誤差の範囲であると言えそうです。
このように標準化を使うことで、どんな場合においても平均値を使って検査をすることができます。
t分布
さて、ここで新たな機械を導入しました。設定を5cmとし、5本の棒を生成したところ、以下のような棒が生成されたました。この機械は正常に動いているでしょうか?
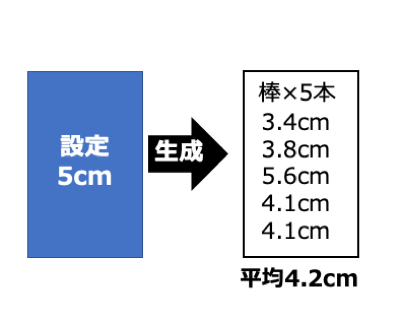
先ほどは、棒の長さを記録する作業を10万回繰り返し、分散1cmの棒が出来上がることが確認されていました。そのため、50本の平均値の分散が1/50cmになることを利用し、Z値を求めることで故障の検査をしました。
しかし、この機械は新製品のため、生成された棒の長さにどれぐらいのばらつきがあるのか分かりません。
ここで、サンプル5本の分散をこの機械が生成する棒のばらつきだと仮定してみましょう。 この機械が生成する棒のばらつきを母分散とすると、不偏分散は
と計算されるので、この0.695を母分散としてz値を求めると
となります。この値を標準正規分布のグラフで表してみると
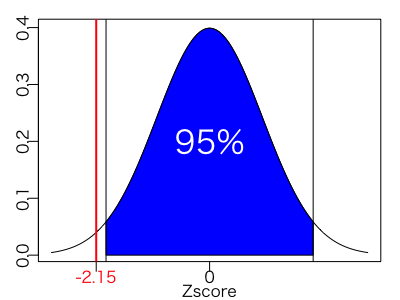
95%より外側になってしまいました。この新しい機械は壊れているのでしょうか?
今回、Z値の分母にある分散にはサンプルから求められる不偏分散を使いました。つまり、一定ではなくサンプルによって変化することになります。
不偏分散を使ったZ値の値と分散を1に固定した場合のZ値の値がどのような分布になるかシミュレーションしてみます。
tvalues <- sapply(1:10000,function(x){ #5個のsampleは平均5,標準偏差1の正規分布から得られているとする samp <- rnorm(5,5,1) #サンプルの不偏分散を使ったz値を計算する (mean(samp)-5)/sqrt(var(samp)/5) }) zvalues <- sapply(1:10000,function(x){ #5個のsampleは平均5,標準偏差1の正規分布から得られているとする samp <- rnorm(5,5,1) #分散を1に固定したz値を計算する (mean(samp)-5)/sqrt(1/5) }) curve(dnorm(x,0,1),-5,5, xlab ="Zscore",ylab ="") hist(zvalues,freq = F ,col = "#00000060",xlim = c(-5,5),main = "",xlab = "",add=T) hist(tvalues,freq = F,col = "#00FF0060",breaks =seq(min(tvalues), max(tvalues),length=50),add=T)
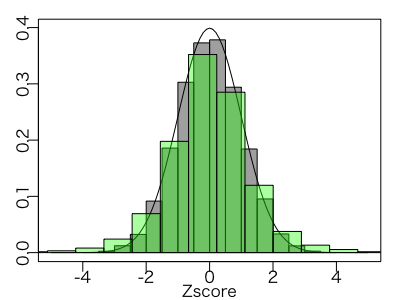
黒色のヒストグラムが分散を固定した場合、緑色が不偏分散を使った場合のヒストグラムです。平均0、標準偏差1の正規分布も重ねてあります。
不偏分散を使った緑のZ値の分布の裾が広くなっていますね。
実は、サンプルの不偏分散を使ってz値を計算した場合は、分散が1より大きな分布になります。これがt分布(t値)です。
このt分布の確率密度関数は非常に難しいので省きますが、サンプルの数(自由度)のみによって分布が決まり、グラフに表すと以下のようになります。
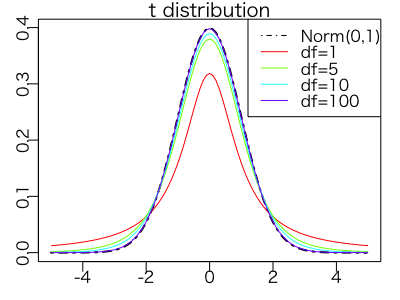
自由度が大きい時は標準正規分布と重なりますが、そうでない場合は裾の大きな分布になっています。これはサンプル数が多いとき、サンプルによる不偏分散の違いが小さく、分散を固定して計算したZ値とほとんど同じになるためです。
先ほどの5本サンプルから計算されたt値を自由度4のt分布で確認してみましょう。
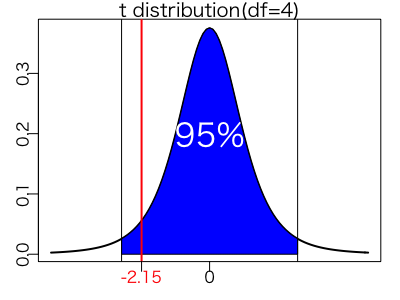
裾が大きくなった分、計算されたt値が95%以内に入りました。この機械は故障しているとは言えなさそうです。
まとめ
今回学んだ正規分布とt分布をまとめておきます。
正規分布
平均値を中心に、左右対称に広がった分布
分布の形を決めるパラメーターは平均と標準偏差

Z値
平均0、標準偏差1の正規分布に従うように基準化された値


t分布
不偏分散を使って計算されたZ値が従う分布
分布の形を決めるパラメーターは自由度のみ

参考
コードを書きながら読んでいくと、とても理解が深まります!

シミュレーションで理解する回帰分析 (Rで学ぶデータサイエンス 20)
- 作者:竹澤 邦夫
- 発売日: 2012/10/10
- メディア: 単行本