線形混合モデルと階層ベイズモデルを使ったデータ解析の実践

前回はベイズ推定を使って単回帰分析を行いました。今回はさらにレベルを上げて階層性のあるデータ解析に挑戦していきます。

medi-data.hatenablog.com

www.medi-08-data-06.work

階層性のあるデータの概略から、通常の単回帰、線型混合モデルそして、階層ベイズモデルを用いたモデリングを行います。

それではいきましょう。

階層性のあるデータとは

そもそも階層性のあるデータとはどのようなデータでしょうか？前回と同じようにテストの点数を勉強時間から推定する場合を考えてみましょう。

今回のデータは生徒数50人のテストの点数と勉強時間を仮定した擬似データセットです。ただし、今回は４校から生徒をランダムにサンプリングしたと仮定しています。

とりあえず、以下を実行してst_df(student_data_frame)というデータセットを作成してみましょう。

library(ggplot2)
library(dplyr)

set.seed(123)
X <- sample(x=5:50, size=50, replace=TRUE)
N_st <- c(20, 14, 10, 6)
school <- rep(1:4, times=N_st)

a0 <- 50
b0 <- 5
a <- a0 + rnorm(4, mean=0, sd=50) 
b <- b0 + rnorm(4, mean=0, sd=10)

data_frame(X=X,school = as.factor(school),
           a=a[school],b=b[school]) %>% 
  mutate(Y=rnorm(50,a+b*X,50)) %>% 
  select(X,school,Y)-> st_df
> st_df
# A tibble: 50 x 3
       X school     Y
   <int> <fct>  <dbl>
 1    18 1      325. 
 2    41 1      726. 
 3    23 1      403. 
 4    45 1      783. 
 5    48 1      804. 

> table(st_df$school)

 1  2  3  4 
20 14 10  6

勉強時間X、学校ID(1~4)、点数Yが並ぶ50行のデータセットです。学校ごとにサンプリングされた人数も異なっています。（20人、 14人、 10人、 6人）

まずは、勉強時間とテストの点数の散布図を書いてみます。

st_df %>% 
  ggplot(aes(x=X,y=Y)) +
  geom_point(aes(col = school))

f:id:h-wadsworth02:20190120160333p:plain

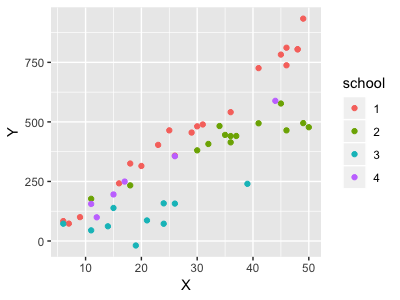
どうやら勉強時間とテストの点数には相関がありそうです。通常の回帰分析を行います。

> #通常の分析
> st_df %>% 
+   glm(data=.,Y~X)

Call:  glm(formula = Y ~ X, data = .)

Coefficients:
(Intercept)            X  
     -65.57        15.32  

Degrees of Freedom: 49 Total (i.e. Null);  48 Residual
Null Deviance:      2824000 
Residual Deviance: 717700  AIC: 626.5

傾き15、切片-65の回帰直線になりましたね。グラフに追加してみましょう。

st_df %>% 
  ggplot(aes(x=X,y=Y)) +
  geom_point(aes(col=school))+
  geom_smooth(method = "lm",se=F)

f:id:h-wadsworth02:20190120160526p:plain

ここまでは通常の回帰分析です。これで勉強時間が１時間増えるほど点数15点増えると言って良いのでしょうか？

よくみると学校3に属する生徒に関しては傾きが緩いようです。しかし、そのことはモデルには反映されていません。

これは、学校によらず勉強時間と点数との関係は一定であるという前提に基づいた解析を行ったからです。

しかし、現実世界では基礎学力が高い生徒が集まっていたり、勉強をすればするほど点数が伸びる生徒が集まっていたり学校によって特徴があると考えられます。つまり学校ごとに切片や傾きが異なるのが普通です。

こういった個人データの中に属性があるようなデータを階層性のあるデータと呼びます。

f:id:h-wadsworth02:20190120161444j:plain

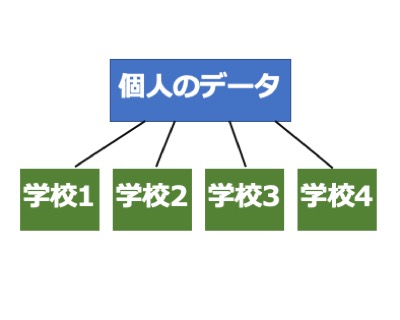
今回は混合モデルと階層ベイズモデルの二つを使って階層性のあるデータを解析していきます。

混合モデル

まずは学校ごとに回帰直線をグラフに書いてみます。

f:id:h-wadsworth02:20190120161636p:plain

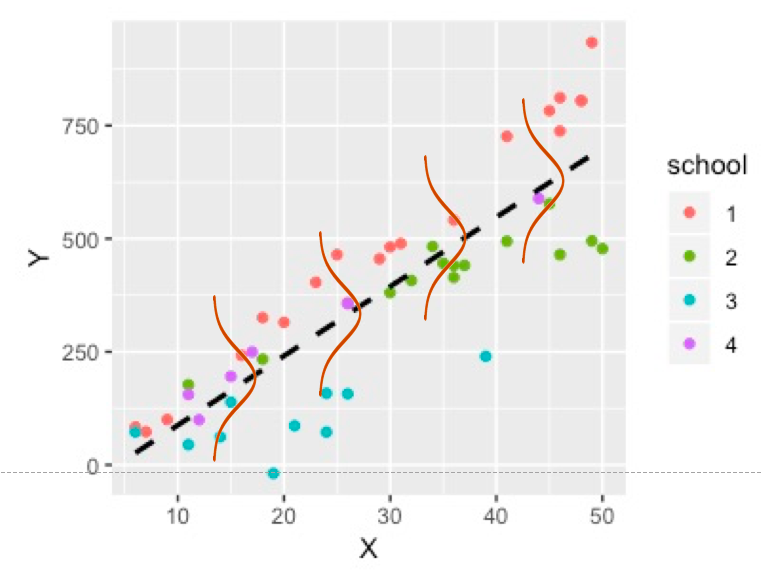
点線が通常の回帰分析の結果を表しています。予想通り、学校ごとで回帰直線の切片と傾きが大きく異なっているようです。

ここで、混合モデルの登場です。通常の回帰分析は、各個人の値それぞれが独立して回帰直線の周りに散らばっているとして推定しています。

イメージとしてはこんな感じです。

f:id:h-wadsworth02:20190120165645p:plain:w450

式で表すと

$Y_{n} = a + b*X_{n} +Normal (0 , \sigma_{student})$

もしくは、

$Y_{n} \sim Normal(a + b*X_{n} , \sigma_{student})$

です。つまり、個人の点数 $Y_{n}$ は、回帰直線上の予測値 $a + b*X_{n}$ に正規分布に従う個人差を足した値として表されます。

混合モデルでは、この回帰直線から個人の値までのバラツキを個人差と学校差に分けて考えます。

式で表すと

$Y_{n} = a_{school} + b_{school}*X_{n} +Normal (0 , \sigma_{student})$

$a_{school}= a_{全体平均}+Normal(0,\sigma_{\alpha})\\ b_{school} = b_{全体平均}+Normal(0,\sigma_{b})$

つまり、回帰直線の切片と傾きにも正規分布に従う学校差によるバラツキを反映させるというのが、混合モデルになります。イメージとしてはこんな感じです。

f:id:h-wadsworth02:20190126181517p:plain:w450

Rで混合モデルを実行するにはいくつかパケージがあるのですが、今回は{lme4}のlmer関数をを使います。

lmer関数の書き方は、lmer(目的変数~説明変数+(説明変数 | 属性))と書きます。(説明変数 | 属性)は属性のバラツキを説明変数の切片と傾きに反映させろという意味です。

実際にやってみましょう。

>library(lme4)
> st_df %>% 
+   lme4::lmer(data=.,Y~X+(X|school)) -> mix_model

> mix_model %>% 
+   summary()
Linear mixed model fit by REML ['lmerMod']
Formula: Y ~ X + (X | school)
   Data: .

REML criterion at convergence: 532.1

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.64401 -0.43795 -0.03278  0.59689  2.08965 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 school   (Intercept) 3272.14  57.203        
          X             30.88   5.557   -0.54
 Residual             2026.92  45.021        
Number of obs: 50, groups:  school, 4

Fixed effects:
            Estimate Std. Error t value
(Intercept)    5.811     33.468   0.174
X             11.649      2.853   4.083

Correlation of Fixed Effects:
  (Intr)
X -0.555

Random effectsとあるのが、切片と傾きのバラツキを表しています。今回の場合は切片の標準偏差が57ぐらい、傾きの標準偏差が5ぐらいなので、勉強時間0時間の基礎学力は学校によってだいたい57点のバラツキがあり、勉強時間と点数の関係は5点ぐらいはバラツキがあるということになります。

そして、Fixed effectsが全体の回帰式の切片と傾きになります。通常の回帰式と今回の結果を比べてみましょう。

lmerで作成されたモデルは特殊な形式になっているので、値を取り出すにはsummaryを変数に代入するか、{lme4}のfixef関数を使います。

>#通常の回帰式
> lm_model$coefficients
(Intercept)           X 
  -65.56781    15.31979 

>#線形混合モデル
> fixef(mix_model)
(Intercept)           X 
   5.810525   11.649468

>#グラフ化
st_df %>% 
  ggplot(aes(x=X,y=Y)) +
  geom_point(aes(col=school))+
  geom_smooth(method = "lm",se=F,col="black",linetype=2)+
  geom_abline(intercept = fixef(mix_model)[1],
              slope = fixef(mix_model)[2],col="black",size=1)

f:id:h-wadsworth02:20190120162428j:plain

混合モデルの結果では、切片が5.8、傾きが11.64と通常の回帰式よりも緩やかになりました。これは、学校差を考慮したことで、個人差の範囲では反映されなかった学校3の値がモデルに反映されたからでしょう。

以上が混合モデルによる解析です。混合モデルを使った解析はまだまだ奥が深いので、そのうち記事にします。

ベイズ推定

さて、次はみなさんお待ちかね階層ベイズモデルです。

まずは概略から説明していきます。通常の単回帰ベイズ推定では、すでに分かっている点数(Y)と勉強時間(X)から、回帰直線パラメーターの確率分布 $p(a,b,\sigma\,|\, Y,X)$ を求めることを行いました。

$p(a,b,\sigma\,|\, Y,X) \propto p(Y,X\,|\, a,b,\sigma)\times p(a,b,\sigma)$

こちらを参考

今回は、事前分布である $p(a,b)$ にも事前分布を仮定します。

$p(a,b,\sigma\,|\, Y,X) \propto p(Y,X\,|\, a,b,\sigma)\times p(a,b,\sigma| \sigma_{a},\sigma_{b})\times p(\sigma_{a}) \times p(\sigma_{b})$

つまり、傾きと切片もパラメーター $\sigma_{a},\sigma_{b}$ によって確率的に変動する値となります。

この事前分布の事前分布（ややこしい...,）は超事前分布と呼び、分布が階層構造になっているため、階層ベイズモデルと呼ばれます。

f:id:h-wadsworth02:20190120162956p:plain

これを式で表すと

$Y_{n} \sim Normal(a_{school} + b_{school}*X_{n}, \sigma_{student})$

$a_{school} \sim Normal(a_{全体平均},\sigma_{\alpha})\\ b_{school} \sim Normal(b_{全体平均},\sigma_{b})$

これは、先ほどの混合モデルの式と意味は同じですね。

$Y_{n} = a_{school} + b_{school}*X_{n} +Normal (0 , \sigma_{student})$

$a_{school}= a_{全体平均}+Normal(0,\sigma_{\alpha})\\ b_{school} = b_{全体平均}+Normal(0,\sigma_{b}$

階層ベイズモデルは、切片と傾きの学校差を確率分布のバラツキとして表現したモデルになります。

上記をstanで実装していきましょう。

data{
  int N;//生徒数
  int K;//学校数
  real<lower=0> X[N];//勉強時間
  real Y[N]; //点数
  int<lower=1,upper=K> school[N];
  
}

parameters{
  real a0;//切片の全体平均
  real b0;//傾きの全体平均
  real a[K];//学校Kの切片
  real b[K];//学校Kの傾き

  real <lower=0> sig_a;//切片のバラツキ
  real <lower=0> sig_b;//傾きのバラツキ
  real <lower=0> sig_st;//個人差のバラツキ
}

model{
  //超事前分布のモデル
  for(k in 1:K){
    a[k] ~ normal(a0,sig_a);
    b[k] ~ normal(b0,sig_b);
  }

 //事前分布のモデル
  for(n in 1:N){
    Y[n] ~ normal(a[school[n]]+b[school[n]]*X[n],sig_st);
  }
}

上記をstratified.stanとして保存します。Rスクリプトに戻り、以下を実行します。

stratified <- stan_model("stratified.stan")

data = list(N=50,K=4,X=st_df$X,Y=st_df$Y,
            school=as.numeric(as.character(st_df$school)))

stf_model <- sampling(stratified,data=data)

収束後に私の環境では

警告メッセージ: 1: There were 384 divergent transitions after warmup. Increasing adapt_delta above 0.8 may help. See http://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup 2: Examine the pairs() plot to diagnose sampling problems

という警告が出ましたが、収束に問題はないので無視してもいいみたいです。

さて、結果を確認してみましょう。

#結果を格納
>stf_res <- rstan::extract(stf_model)

> #データフレームに形成
> data.frame(a0=stf_res$a0,b0=stf_res$b0,
+                 sig_a=stf_res$sig_a,sig_b=stf_res$sig_b) %>% 
+   #平均値を算出
+   apply(2,mean)
       a0        b0     sig_a     sig_b 
  8.13921  11.71920 110.18663  10.63632

切片が約8、傾きが約12、学校差による切片の標準偏差が110ぐらい、傾きの標準偏差が11ぐらいとなりました。混合モデルよりも標準偏差が大きくなっていますが、切片と傾きの推定値はだいたい同じになりました。

グラフに加えてみましょう。

f:id:h-wadsworth02:20190120163254j:plain

赤色がベイズ推定の結果になります。ほとんど同じですね。

また、回帰係数の切片と傾きのベイズ95%信用区間と混合モデルの95%信頼区間を比較してみます。

混合モデルの信頼区間は{bloom}パッケージのtidyを使うと表示できます。

>#a0とb0の95%信用区間
> data.frame(a0=stf_res$a0,b0=stf_res$b0,
+            sig_a=stf_res$sig_a,sig_b=stf_res$sig_b) %>% 
+   apply(2,function(x){
+     c(mean=mean(x),
+       quantile(x,prob=c(2.5,97.5)/100))
+   })
              a0         b0      sig_a     sig_b
mean     8.13921 11.7192006 110.186633 10.636319
2.5%  -134.64597 -0.2067318   2.956362  3.336309
97.5%  177.83454 24.3158309 429.429429 33.796667

>#混合モデルの95%信頼区間
>library(bloom)
> tidy(mix_model,effects="fixed",conf.int=T)-> coef_mix
#見やすいように整形
> data.frame(x=c("mean","2.5%","97.5%"),
+            a0 = c(coef_mix$estimate[1],coef_mix$conf.low[1],coef_mix$conf.high[1]),
+            b0 = c(coef_mix$estimate[2],coef_mix$conf.low[2],coef_mix$conf.high[2]))
      x         a0        b0
1  mean   5.810525 11.649468
2  2.5% -59.784677  6.057005
3 97.5%  71.405726 17.241931

階層ベイズモデルの方が幅が広く推定されているみたいですね。切片と傾きのバラツキ(sig_a,sig_b)も確率分布として表現できるのも階層ベイズの凄さです。

また、傾きb0の95%信用区間に負の値が含まれているため、必ずしも勉強時間が増えたからと言って、点数が伸びる訳ではなさそうです。

さらに、sig_a,sig_bの超事前分布には何も指定しなかったので、無情報分布として推定されましたが、他の分布を仮定することもできます。

例えば、切片、つまり勉強時間が0時間の基礎学力のバラツキが2.9~429ととても広く推定されています。そこで、学校による基礎学力差のバラツキは100点ぐらいのはずだという仮定をモデルに組み込んでみます。

どうするかというと、超事前分布に標準偏差100、自由度3or4の半t分布を使用します。（半t分布は標準偏差の事前分布として推奨されている）

半t分布とはt分布の中で0以上の値のみを仮定する分布なのですが、sig_aで<lower=0>を仮定しているので、必然的に半t分布になります。（正規分布の場合はさらに仮定が強くなる）

イメージとしては以下の図のような形で、0~100の間に多くの値が集まっていてて、遠くに離れるほどその確率密度が小さくなるような分布です。

f:id:h-wadsworth02:20190120164100p:plain

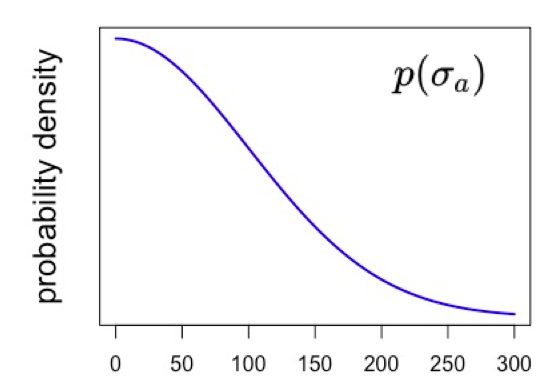
stanコードのmodelブロックに以下のように追加し、stratifed2.stanとして保存します。

data{
  int N;//生徒数
  int K;//学校数
  real<lower=0> X[N];//勉強時間
  real Y[N]; //点数
  int<lower=1,upper=K> school[N];
  
}

parameters{
  real a0;//切片の全体平均
  real b0;//傾きの全体平均
  real a[K];//学校Kの切片
  real b[K];//学校Kの傾き

  real <lower=0> sig_a;//切片のバラツキ
  real <lower=0> sig_b;//傾きのバラツキ
  real <lower=0> sig_st;//個人差のバラツキ
}

model{
  sig_a ~ student_t(4,0,100);//t分布を仮定
  //超事前分布のモデル
  for(k in 1:K){
    a[k] ~ normal(a0,sig_a);
    b[k] ~ normal(b0,sig_b);
  }

 //事前分布のモデル
  for(n in 1:N){
    Y[n] ~ normal(a[school[n]]+b[school[n]]*X[n],sig_st);
  }
}

Rで実行してみます。

stratified2 <- stan_model("stratified2.stan")

stf_model2 <- sampling(stratified2,data=data)

> #結果を格納
> stf_res2 <- rstan::extract(stf_model2)
> data.frame(a0=stf_res2$a0,b0=stf_res2$b0,
+            sig_a=stf_res2$sig_a,sig_b=stf_res2$sig_b) %>% 
+   apply(2,function(x){
+     c(mean=mean(x),
+       quantile(x,prob=c(2.5,97.5)/100))
+   })
              a0        b0    sig_a    sig_b
mean    4.381098 11.806118  71.2029 11.75319
2.5%  -83.411036 -2.502853  14.0425  3.16490
97.5%  96.946187 28.298460 181.9355 44.53861

#先ほどのモデル
              a0         b0      sig_a     sig_b
mean     8.13921 11.7192006 110.186633 10.636319
2.5%  -134.64597 -0.2067318   2.956362  3.336309
97.5%  177.83454 24.3158309 429.429429 33.796667