じっくり学ぶ時系列解析~見せかけにだまされない編~ - 医療職からデータサイエンティストへ

時系列モデルを作るときは、データが定常過程に従っていることを前提とするモデルが多いです。しかし、現実には定常過程に従うデータはあまり多くありません。そんな非定常過程のデータを何となく多変量モデルで解析すると一見ものすごく当てはまりの良いモデルができてしまうことがあります。

今回は、そんな見せかけに騙されないためにも、時系列モデルを作る際に重要な単位根や共和分などの概念ををまとめたいと思います。

書籍等では難しい数式が並びますが、概念自体は直感的にも理解しやすいのです。

単位根とランダムウォーク
- ADF検定
  - 補足：ADF検定について少し詳しく
単位根はなにが問題か~見せかけの回帰問題~
- 補足：見せかけの回帰に騙されない方法
共和分
共和分の検定
Rでの実践
まとめ
参考書籍
その他

単位根とランダムウォーク

非定常過程というとよく出てくるのが単位根過程とランダムウォークです。どんなものかというと、こんなんです。

f:id:h-wadsworth02:20190309114825j:plain

これは以前の記事で紹介した来月の売上を今月の売上から予測するためのアイスの売り上げモデルです。

$y_{来月の売上} = y_{今月売上} + \epsilon_{今月}$

www.medi-08-data-06.work

単位過程とは係数が1を含むAR過程とも言えます。AR過程の係数が１未満であると定常過程になるのは、平均値から大きくずれた時点があったとしても係数が1未満であれば、その影響はいずれ0になるので、結果的に平均回帰的になるからです。

例えば、こんなAR過程であるt時点で偶然にも20という値になったとしましょう。誤差正規分布の標準偏差が5であるため、20以上の値が出る確率は、0.00003%ぐらいです。

$y_{t} = 0.5y_{t-1} + \epsilon_{t}=20\, , \epsilon_{t} \sim Normal (0 , 5)$

するとt+1時点目の値は、

$y_{t+1} = 0.5 \times 20 + \epsilon_{t+1} = 10 + \epsilon_{t+1}$

となります。さらにt+2,t+3時点目を計算していくと

$y_{t+2} = 0.5(10 + \epsilon_{t+1})+\epsilon_{t+2} = 5 + 0.5\epsilon_{t+1}+\epsilon_{t+2}$

$y_{t+3} = 0.5(5 + 0.5\epsilon_{t+1}+\epsilon_{t+2})+\epsilon_{t+3} = 2.5 + 0.25\epsilon_{t+1}+0.5\epsilon_{t+2}+\epsilon_{t+3}$

と20という影響がだんだん無くなっているのが分かります。誤差に関しても、式をみてわかるようにどんどん0に近づいていきます。（実はAR過程は無限のMA過程に書き換え可能であり、これは重要な特性なのですが今回は触れないので下記参考書をご参照下さい。）

次に以下のような単位根過程で、同じようにあるt時点で20の値をとった場合のことを考えてみましょう。

$y_{t} = y_{t-1} + \epsilon_{t}= 20\,, \epsilon_{t} \sim Normal (0 , 5)$

t+1時点目は

$y_{t+1} = 20 + \epsilon_{t+1}$

同様にt+2,t+3時点目は

$y_{t+2} = 20 + \epsilon_{t+1}+\epsilon_{t+2}$

$y_{t+2} = 20 + \epsilon_{t+1}+\epsilon_{t+2}+\epsilon_{t+3}$

となりt時点目の20の影響はずっと残ったまま、しかも誤差もどんどん足し算されています。これをランダムウォークとも言い、どこに値があるのかはランダムに決定されることから、この名前がついています。

つまり、単位根過程の場合には長期的な予測は全くできないことになります。(定常過程であれば、平均に収束します。)

現実世界では、株価などが単位根過程の代表ですね。株価の長期的な予測は誰にもできないことで知られています。

以前の記事でも紹介したように、モデリングするときには、定常過程になるようにデータを前処理をするのが定石パターンです。（状態空間モデルや閾値ARモデルなど、非定常過程をそのままモデリングする例外もあります。）

www.medi-08-data-06.work

ADF検定

ところで単位根過程にデータが従うことはどのように調べれば良いでしょうか？過程が定常過程かそうではないかの判断方法は、時系列解析の長い歴史の中で多くの研究がなされ、様々な手法が考案されてきました。

その中でももっとも一般的なものがADF検定(Augmented Dickey Fuller test)です。ADF検定は、AR過程において、"係数が1である"を帰無仮説として、"係数が１未満である"を対立仮説とするため、この検定で棄却された場合は定常過程であると言えます。

棄却できなかったとしても、単位根を持つとは積極的に言えないことに注意してください。

補足：ADF検定について少し詳しく

ADF検定は、次数が1の場合を検定するためのDF検定を次数が１以上にも対応できるように拡張したものです。基本的な考え方はDF検定に基づくため、DF検定の枠組みで説明します。

まず、DF検定の帰無仮説は"AR(1)過程の係数が1である"を設定します。そして対立仮説では以下の3つからもっともらしそうな対立仮説を選びます。

過程の期待値が0で、トレンドがない :

$y_{t} = \rho y_{t-1}+\epsilon_{t}\,,\rho \lt 1$

過程の期待値が0ではなく（定数項をもち）、トレンドがない :

$y_{t} =c+ \rho y_{t-1}+\epsilon_{t}\,,\rho \lt 1$

過程の期待値が0ではなく（定数項をもち）、トレンドがある :

$y_{t} =c+ \rho y_{t-1}+\beta t+\epsilon_{t}\,,\rho \lt 1$

上から下に行くほど前提が緩くなり、誤って棄却してしまうことが少なくなります。（単位根を定常過程であると判断してしまう。）しかし、逆にいうと検定力が落ちるので、定常過程であっても棄却されない可能性が高くなります。

特段の理由がなければ一番緩い仮定の3番目を対立仮説としますが、前提が確実な場合はそれ以外も検討すると良いでしょう。

ADF検定は、基本的な流れはDF検定と同じですが、次数の選択をする必要があります。

次数選択の方法に関しても様々な考え方がありますが、AICなどの情報量基準に基づくのが一般的なようです。

単位根はなにが問題か~見せかけの回帰問題~

株価などの単位根過程に従う場合には、モデル作成や予測はできないことが分かりました。しかし、なんとか他の変数を使ってでも値の動きを説明したいと思うのが、人間の欲望ってものです。

そこである変数Xを使って、単位根過程に従うデータYに対して回帰式を作ってみましょう。こんな感じです。

$Y_{t} = \beta X_{t}+\epsilon_{t}$

もしこんな回帰式ができたとして、変数Xを手に入れることが可能なら、ランダムウォークに従うはずのYの値を説明できることになります。

実はこんな理想的な回帰式を作ることのできるXは誰でも手に入れることができるのです。それは、同じようにランダムウォークに従うデータをXにして回帰式を作れば良いのです。

つまり実際はなんの関係もないランダムウォーク同士を回帰式にすると、とても当てはまりの良い回帰式ができることが分かっています。これを見せかけの回帰と言います。

これは二つの単位根過程従うデータをプロットしてものです。二つの企業の株価とでもしましょうか。この赤と黒のデータを回帰式にすると係数が優位な回帰式ができますが、ご覧の通り全く意味はありませんね。

時系列

単位根過程のあるデータは前処理をして定常過程にしてから、統計モデルを作りましょう。定常過程のモデルであれば、因果の推論やその他多変量モデルのテクニックを使うことができます。

www.medi-08-data-06.work

補足：見せかけの回帰に騙されない方法

見せかけの回帰かどうかを判断するためには、変数同士が単位根過程に従うことを確認すれば騙されずに済みますが、後述する共和分との兼ね合いもあります。もう一つ見せかけの回帰かそうではないかを確かめる方法として、DW検定(Durbin Watson test：ダービンワトソンテスト)と呼ばれるものがあります。

DW検定自体は、見せかけの回帰のためというよりも、一変量、多変量モデル問わず、作ったモデルの残差に自己相関があるかどうかを検定するためのものです。（モデルの残差に自己相関がある場合は、良いモデルではない）

見せかけの回帰の場合、推定された係数が優位であり、決定係数も高くなりがちですが、残差の自己相関は無くなりません。試しに先ほどの二変数で回帰式を作り、モデルの残差をコレログラムにしたものが以下になります。

時系列

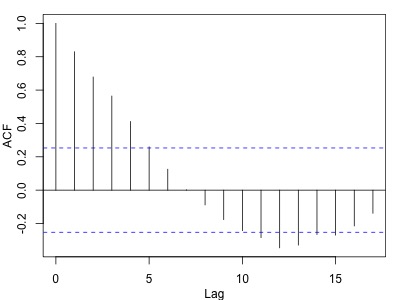
思いっきり自己相関がありますね。DW検定は残差に自己相関がないことを帰無仮説とするため、回帰式にDW検定を行って棄却されれば、残差に自己相関が存在することが確認でき、見せかけの回帰であると判断できます。

共和分

さて、単位根過程同士の回帰式は意味がないことが分かりました。しかし、意味のある回帰式ができる時があります。それは変数間に共和分の関係が成り立つ時です。

一変量時系列モデルの時、差分をとった場合に定常過程になる過程（ARIMAモデルなど）を和分過程と言いました。

共和分とは和分過程を二変量以上に拡張し、単位根に従う二つの変数同士がうまく打ち消しあって定常過程に従う場合のことを指します。

イメージが掴みにくいと思うので、以下をみてみてください。

時系列

赤と黒が似たような動きをしているように見えます。これが共和分の関係にある変数です。

赤も黒も単位根過程に従うため、各変数のみでARIMAモデルなどの一変量時系列モデルを作ることはできません。しかし、赤と黒で回帰式を作ると意味のあるモデルになるのです。赤と黒の変数で回帰式を作り、残差のをプロットしてみましょう。

時系列

なんとなく定常過程っぽいですね。これは単位根の変数同士がうまく打ち消しあっているため、作成した回帰式の残差は定常過程になります。

ちなみに見せかけの回帰式残差は単位根過程になり、こんな感じになります。

時系列

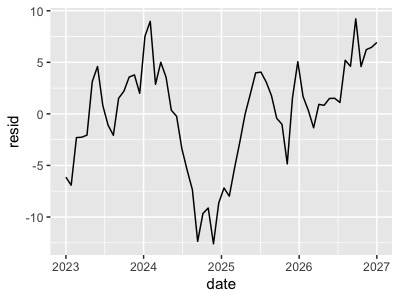
共和分の関係にあるということは、それぞれの変数が均衡していると解釈することもできます。この共和分の関係を使って株の取引を行うペアトレードという手法があります。これは単体の株価を予測することは難しくても、共和分の関係にある株価の差（グラフ青矢印）の期待値は同じなるため、差が大きすぎたり小さすぎたりした場合には、それぞれの株を売り買いするというものです。

共和分の検定

二変数同士が共和分の関係になるためにはどのような検定をすれば良いでしょうか。とりあえず二変数同士が単位根過程に従うことを前提とします。

一つは相関係数をみるという手もあります。片方が大きくなればもう片方も大きくなるため相関係数も高くなります。しかし、共和分への十分条件ではないため、他の方法を検討します。

作ったモデルの残差に単位根検定をするのはどうでしょうか？共和分の関係であれば、残差は定常過程に従うはずなので、残差に対してADF検定をすれば良いでしょう。

この考えに基づいたのがEngel – Granger 検定です。棄却点は異なりますが、考え方は変わりません。

詳細は省きますが、さらに進化した検定としてはJohasen型の共和分検定というものがあり、これは二変数以上の共和分も考慮できる検定です。

興味のある方は下記参考書をご覧ください。

Rでの実践

単位根とADF検定

RでADF検定を行うには{tserese}パッケージのadf.test{tserise}、もしくは{urca}パッケージのur.df{urca}を使います。一般的にはadf.testが使われているようですが、最初からトレンド、定数項付きの検定しかできません。ur.dfでは、定数項やトレンドの有無や仮定するlag数を指定できるため、こちらの方が柔軟性が高いです。共和分の検定にも{urca}パッケージを使うため今回はur.dfを使ってADF検定を行います。

library(dplyr)
library(ggplot2)
library(urca)
#単位根に従うデータの作成

set.seed(123)
year <- 5
date <- seq(ymd("2023/1/1"),ymd("2027/1/1"),length.out  = 12*year )
y <- rep(0,12*year) 
x <- rep(0,12*year)
epsy <- rnorm(12*year,0,3)
y[1] <- 50
for(i in 2:(12*year)){
  y[i] <- y[i-1]+epsy[i]
}

#ADF検定
#typeには"none","drift""trend"を指定できる。今回は一番安全なtrendを使う。（定数項、トレンド付きを仮定）

> ur.df(y,type=c("trend")) %>% summary()

############################################### 
# Augmented Dickey-Fuller Test Unit Root Test # 
############################################### 

Test regression trend 


Call:
lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.6688 -1.7413 -0.0524  1.2129  7.0323 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept)  3.58826    2.38388   1.505    0.138
z.lag.1     -0.05828    0.04240  -1.375    0.175
tt          -0.01781    0.01981  -0.899    0.373
z.diff.lag   0.08654    0.13467   0.643    0.523

Residual standard error: 2.497 on 54 degrees of freedom
Multiple R-squared:  0.04756,    Adjusted R-squared:  -0.005353 
F-statistic: 0.8988 on 3 and 54 DF,  p-value: 0.4479


Value of test-statistic is: -1.3745 0.8144 1.2215 

Critical values for test statistics: 
      1pct  5pct 10pct
tau3 -4.04 -3.45 -3.15
phi2  6.50  4.88  4.16
phi3  8.73  6.49  5.47

Value of test-statistic isの後に並ぶ最初の-1.374とtau3をみます。有意水準10%の値が-3.15であるため、今回は棄却されませんでした。つまり定常過程とは言えず、単位根過程の可能性があるということですね。

参考にadf.testも使ってみます。

library(tserise)
> adf.test(y)

    Augmented Dickey-Fuller Test

data:  y
Dickey-Fuller = -1.3651, Lag order = 3, p-value =
0.8314
alternative hypothesis: stationary

alternative hypothesis: stationaryは対立仮説は定常であるという意味なので、こちらでもp値が0.8で棄却されませんでした。

見せかけの回帰

もう一つ単位根過程をつくって回帰式を作ってみます。

set.seed(123)
year <- 5
x <- rep(0,12*year)
epsx <- rnorm(12*year,0,3)

x[1] <- 50
for(i in 2:(12*year)){
  x[i] <- x[i-1]+epsx[i]
}

 uni_lm <- lm(y~x)
> uni_lm %>% summary()

Call:
lm(formula = y ~ x)

Residuals:
     Min       1Q   Median       3Q      Max 
-12.1605  -5.3995   0.1769   4.3908  14.7097 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  81.0117     6.2322  12.999  < 2e-16 ***
x            -0.7137     0.1522  -4.691  1.7e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 6.746 on 58 degrees of freedom
Multiple R-squared:  0.275,  Adjusted R-squared:  0.2625 
F-statistic:    22 on 1 and 58 DF,  p-value: 1.7e-05

なんと、本当は無関係なはずの変数間にとても有意な回帰係数が推定されました。 DW検定と残差の自己相関コレログラムを書いてみましょう。DW検定には{lmtest}のdwtest{lmtest}を使い、作った回帰式をそのまま渡します。

#残差のコレログラム
> acf(uni_lm$residuals)

> dwtest(uni_lm)

    Durbin-Watson test

data:  res
DW = 0.23908, p-value < 2.2e-16
alternative hypothesis: true autocorrelation is greater than 0

時系列

コレログラムは思いっきり自己相関がありますね。DW検定でも自己相関がないという帰無仮説が棄却され、自己相関があるという結果になりました。

これが見せかけの回帰の特徴です。

共和分

さて最後は共和分をRで実装、検定していきましょう。Engel – Granger 検定はca.po{urca}を使います。また、共和分は二変数を線形の関係で表すことができる、つまり、

$y_{t} = \beta x_{t} + \epsilon_{t}\,, \epsilon \sim Normal(0,\sigma)$

という式が成り立てば良いので、先ほど作ったXの変数からYを作成します。一応単位根検定もしておきましょう。

set.seed(123)
#係数は適当に0.8をかけてyを作る
y <- 0.8*x+rnorm(12*year,0,3)

#一応単位根検定
> ur.df(y,type = "trend") %>% summary()

############################################### 
# Augmented Dickey-Fuller Test Unit Root Test # 
############################################### 

Test regression trend 


Call:
lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)

Residuals:
     Min       1Q   Median       3Q      Max 
-12.0280  -3.0916  -0.2166   2.8258   9.2086 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)  7.29048    3.94575   1.848   0.0701 .
z.lag.1     -0.19271    0.10668  -1.806   0.0764 .
tt           0.01471    0.03925   0.375   0.7094  
z.diff.lag  -0.31223    0.13286  -2.350   0.0225 *
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.411 on 54 degrees of freedom
Multiple R-squared:  0.2197, Adjusted R-squared:  0.1764 
F-statistic: 5.069 on 3 and 54 DF,  p-value: 0.003639


Value of test-statistic is: -1.8064 1.1898 1.7778 

Critical values for test statistics: 
      1pct  5pct 10pct
tau3 -4.04 -3.45 -3.15
phi2  6.50  4.88  4.16
phi3  8.73  6.49  5.47

統計量-1.80、有意水準10%の値が-3.15で棄却されませんでした。定常過程とは言えなさそうです。

Engel – Granger 検定を行います。データは二変数のデータフレームにして渡すことに注意してください。また、引数のdemeanでは、線形の関係性を指定します。指定できるものには以下があり、共和分の関係イメージとしてはこんな感じになります。（赤色がX、黒色がY）

"none" ：トレンドも定数項（切片もない）

$y_{t} = \beta x_{t} + \epsilon_{t}$

時系列

"const"：定数項のみある

$y_{t} = c + \beta x_{t} + \epsilon_{t}$

時系列

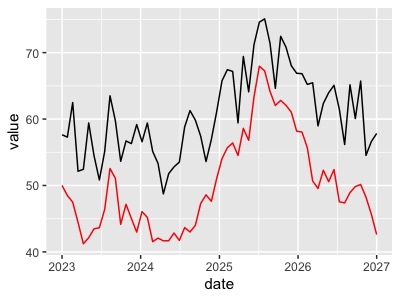
"trend"：定数項とトレンドがある

$y_{t} =c+trend+ \beta x_{t} + \epsilon_{t}$

時系列

やってみましょう。

>ca.po(data_frame(y,x),demean = "trend") %>% summary()

######################################## 
# Phillips and Ouliaris Unit Root Test # 
######################################## 

Test of type Pu 
detrending of series with constant and linear trend 


Call:
lm(formula = z[, 1] ~ z[, -1] + trd)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.7682 -1.7898  0.0126  1.7528  5.8962 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.787699   2.590220  -0.690    0.493    
z[, -1]      0.840724   0.055463  15.158   <2e-16 ***
trd         -0.001976   0.022798  -0.087    0.931    
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.764 on 57 degrees of freedom
Multiple R-squared:  0.8308, Adjusted R-squared:  0.8249 
F-statistic:   140 on 2 and 57 DF,  p-value: < 2.2e-16


Value of test-statistic is: 56.9265 

Critical values of Pu are:
                  10pct    5pct    1pct
critical values 41.2488 48.8439 65.1714

今回は定数項もトレンドもないモデルだったので、定数項(intercept)とトレンド(trd)は有意な係数ではありません。こいった場合には"none"を指定すれば良いでしょう。

#noneを指定してやり直し
> ca.po(data_frame(y,x),demean = "none") %>% summary()

######################################## 
# Phillips and Ouliaris Unit Root Test # 
######################################## 

Test of type Pu 
detrending of series none 


Call:
lm(formula = z[, 1] ~ z[, -1] - 1)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.3468 -2.1275  0.0167  2.2013  7.7618 

Coefficients:
        Estimate Std. Error t value Pr(>|t|)    
z[, -1] 0.798886   0.008382   95.31   <2e-16 ***
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.293 on 59 degrees of freedom
Multiple R-squared:  0.9935, Adjusted R-squared:  0.9934 
F-statistic:  9083 on 1 and 59 DF,  p-value: < 2.2e-16


Value of test-statistic is: 51.5311 

Critical values of Pu are:
                  10pct    5pct    1pct
critical values 20.3933 25.9711 38.3413

共和分の結果は一番下Value of test-statistic is: に出ています。今回の統計量51.53対して、有意水準1%の値が38.34であるため、帰無仮説が棄却され共和分の関係にあるといって良さそうですね。trendを指定した上の結果は5%水準では棄却されていますが、1%水準では棄却されていません。

ちなみにJohasen型の共和分検定を行うにはco.jo{urca}を使います。