機械学習モデルは、統計モデルよりも予測に長けた手法であり、皆様もご存知の通り様々な場面で用いられています。一方で、結果の解釈の面ではブラックボックスになりやすいため、モデルの作成時のみならず、機械学習に覚えのない方々とコミュニュケーションをする上でも重要な課題です。
そんな、機械学習モデルと対話するためのツールがSAHP値(SHapley Additive exPlanation Values)です。SHAPを使うと、機械学習モデルが特徴量をどのように使って予測をしたのか、特徴量は予測結果にどれぐらい影響を与えているのか、などをデータ全体(Global)、さらに個別のサンプルごと(Individual)に確認することができます。今回はSHAPを使って、学習した機械学習モデルと対話してみましょう。
今回は主に以下を参考にしました。
そもそもSHAPってなんぞ??
SHAPを使い始める前に、そもそもSHAPとは何を表すかというと、個別のサンプルごとの予測値が、特徴量からどれぐらい影響を受けているかを数値化した値のことです。例えば、
のような単純な回帰モデルであれば、特徴量はそれぞれ、予測結果
に対して、平均的に+10と-5の影響を与えています。SHAPは個別のサンプルごとに、特徴量の係数が求まっているようなイメージになります。
例えば、Aサンプルの予測値が、
のSHAP値がそれぞれ、4と-1となっていれば、
と予測結果を解釈することができるということです。より詳細なSHAPの理解は、私が書くよりもこちらの記事を読まれると良いです。
SHAP(SHapley Additive exPlanations)で機械学習モデルを解釈する - Dropout
何がともあれ、早速やってみましょう。
adultデータセットで、高収入予測モデルを作る。
まずは、SHAPを使うための機械学習モデルを作っていきます。
今回は、性別や人種、学歴などを含む12個の特徴量から世帯年収が高収入かそうではないかを予測するためのデータセットadultを使って、2値分類の機械学習モデルを作成します。このデータセットは、SHAPにデフォルトでインストールされているのでご安心を。他にも連続量データセットから画像分類用などまで様々なデータセットがあるため、目的に合わせてSHAPの練習をすることができます。
早速予測モデルを作っていきましょう。今回はLight GBMを使って予測モデルを作成します。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import shap from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score import lightgbm as lgb %matplotlib inline #データセットの読込 X,y = shap.datasets.adult() #上記は初めからカテゴリーデータがコード化されているので、元々のカテゴリー名を取得する。 X_display,y_display = shap.datasets.adult(display=True) # create a train/test split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=7) X_test_display = X_display.iloc[X_test.index,:] lgb_train = lgb.Dataset(X_train, label=y_train) lgb_test = lgb.Dataset(X_test, label=y_test) params = { "objective": "binary", "metric": "binary_logloss", } #モデルの学習 lgb_model = lgb.train(params, lgb_train, 10000, valid_sets=lgb_test, early_stopping_rounds=50, verbose_eval=1000) #予測 pred = lgb_model.predict(X_test)
データ量はそこまで多くはないので、学習に時間はかかりません。とりあえず、このモデルの予測結果をaccuracyを使って評価してみます。(本来、モデル学習の際はtestセットをvalidationには使わないのですが、今回はあくまでSHAPがメインですので、ご勘弁を)
print(accuracy_score(np.round(pred),y_test)) >0.8757868877629357
今回のモデルでは、87%の予測精度です。ここまでは、通常の機械学習モデルの作成方法で、特徴量エンジニアリングやハイパラメーターチューニングをしながら予測精度の向上を目指すのが定石となりますが、ここからSHAPを使って機械学習モデルと対話をしていきます。
SHAPの準備
まずは、SHAP値を取得しましょう。
#notebook内でJavascriptを動かすためのおまじない shap.initjs() #modelと解釈したいデータを渡す。 explainer = shap.TreeExplainer(model=lgb_model) shap_values = explainer.shap_values(X=X_test)
TreeExplainerは、決定木系のモデルのSHAP値を取得するためのものです。その他には、
shap.LinearExplainer線形モデル用shap.DeepExplainerディープラーニングモデル用shap.KernelExplainerその他のモデル用
などがあります。shap.KernelExplainerはSVMなどに使えますが、基本的にはどんなモデルでもSHAP値を算出できます。ただし、モデルを仮定しないため計算スピードは遅いみたいです。
さて、SHAP値をshap_valuesに格納しました。分類問題の場合は、それぞれのクラスごとのSHAP値がリストで返ってきます。今回は高収入(クラス1)の予測モデルなので、リストの2つ目を使います。
shap_values[1].shape > (6513, 12)
ご覧の通り、X_test の6513サンプルそれぞれに対して、12の特徴量の寄与度が格納されています。
SHAPの可視化
いよいよSHAPを使っていきましょう。SHAP値の可視化には、様々な方法があるので、目的に合わせて使い分けていきます。
shap.force_plotshap.summary_plotshap.dependence_plotshap.decision_plot
shap.force_plot
早速1人目のサンプルを見てみましょう。個別のサンプルごとにSHAPをみるにはshap.force_plotを使います。
shap.force_plot(explainer.expected_value[1], shap_values[1][0,:], X_test_display.iloc[0,:],link="logit")

第1引数のexplainer.expected_value[1]は予測の平均値を表し、base_value(0.0824)となっています。ここは、任意で数値を与えることもできます。第2引数には1人目のSHAP値を、第3引数には元々の特徴量を渡します(今回は、結果をみやすくするために、コード化されていない方のデータを渡します)。また、今回は、オッズ比でSHAP値が返ってくるので、link="logit"として確率に変換します。
最終的な予測結果は、base_valueからそれぞれの特徴量のSHAP値を足し引きした値となり、1人目の最終的な予測結果は0.05、つまり高収入である確率が5%なので、クラスは0に分類されます。特徴量の影響としては、職業がexec managerであることと、年齢が39歳であることは、予測に対して正方向に影響し、独身、女性、キャピタルゲインがないことなどが負方向に影響しているようです。
また、shap.force_plotは、上記の結果を任意のサンプル数でまとめてみることができます。1000人分のサンプルをみてみましょう。
shap.force_plot(explainer.expected_value[1], shap_values[1][0:1000,:], X_test_display.iloc[0:1000,:],link="logit")
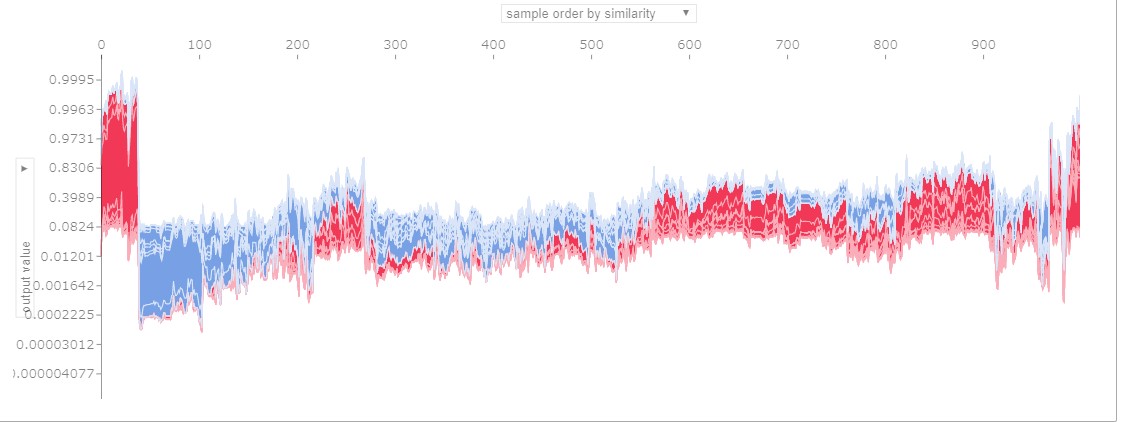
縦軸が予測値、横軸が特徴量が似ているもの同士をまとめて並べた各サンプルを表しています。(1サンプルの時は横向きだった表示を、90度回転させて並べています)横軸の並び順は、予測値の大きさ順、特徴量の大きさ順などに変更することもでき、縦軸も特徴量ごとに絞ることが出来ます。例えば、横軸を左から予測値の大きい順(高収入である確率予測値が大きい順)に、縦軸を年齢とキャピタルゲインの影響度としてみると
年齢の影響
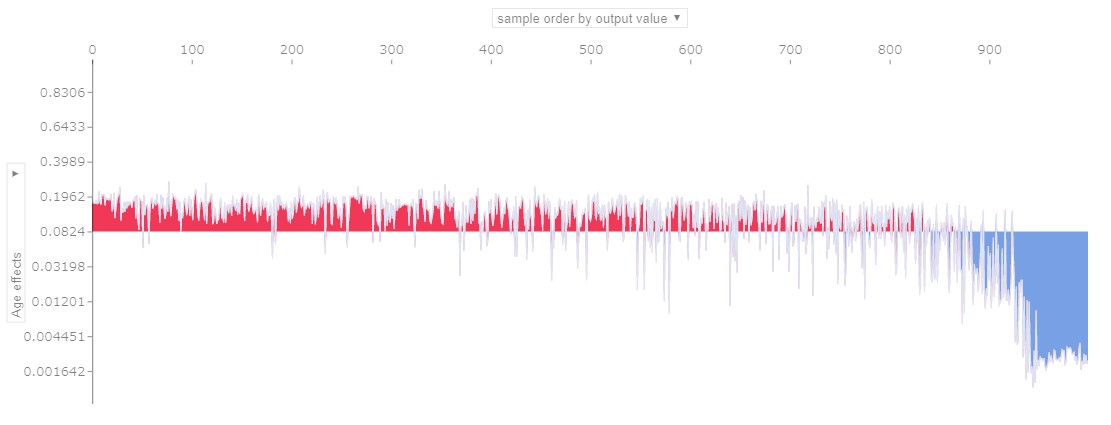
キャピタルゲインの影響
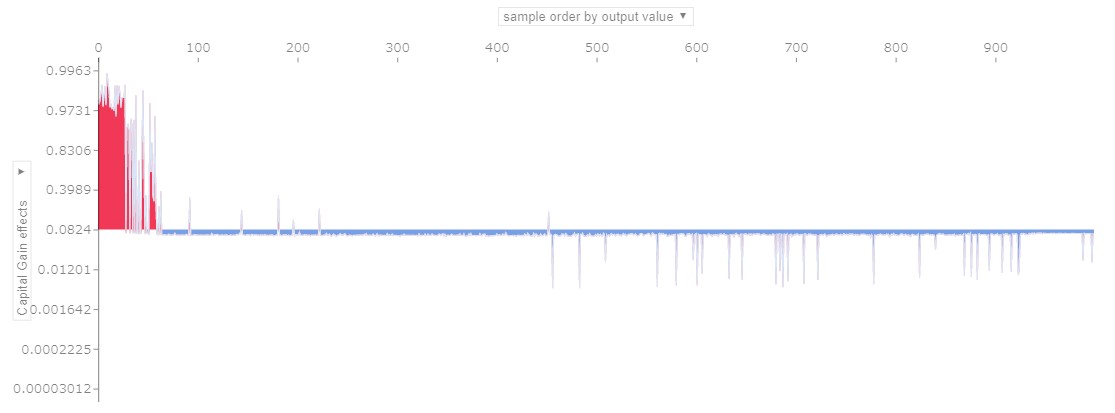
年齢の影響は右側ほど大きく、キャピタルゲインは左側ほど影響力が大きいことが分かります。つまり年齢は、高収入ではない人を、高収入ではないと予測すること(True Negative)に大きく寄与し、キャピタルゲインは、高収入である人を、高収入であると予測すること(True positive)に大きく寄与していることが分かります。
shap.summary_plot
先ほどのshap.force_plotは個別のサンプルごとのindeividualな影響をみるには便利ですが、もっと大局的にGlobalな結果を見たい場合には不向きです。Globalな影響力を確認したいときはshap.summary_plotを使いましょう。
shap.summary_plot(shap_values[1],X_test)
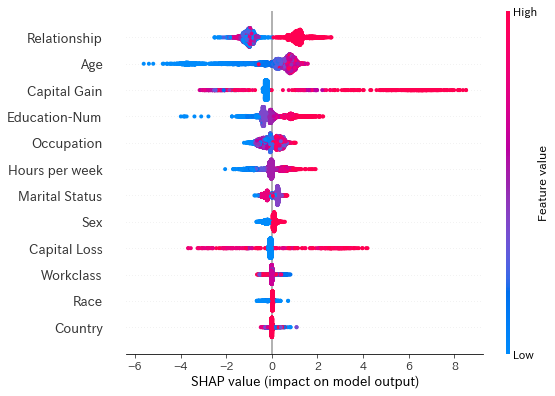
見方としては、点が個々のサンプルを表し、特徴量は予測全体への影響力が大きい順に上から並んでいます。色は特徴量の大きさ、横軸を表しています。例えば年齢は、若い場合は予測に対して負の影響を与えていますが、年をとるごとに正方向へ影響力が変化していることが分かります。Relation Shipなどのコード化された変数は、色の違い(値の大小)に意味がないことに注意しましょう。AgeとCapital Gainは先ほど見た通り、それぞれ正方向、負方向への予測に大きく寄与していることが分かります。
また、それぞれの特徴量がすべてのデータに影響を与えているのか、一部のデータに影響を与えているのかということを読み取ることも出来ます。Capital Lossは、値が小さい場合には、SHAP値が0付近なので予測にほとんど影響しませんが、値が一定額以上になる一部のサンプルに対しては、正方向もしくは負方向の予測に大きく寄与していることが分かります。
shap.dependence_plot
さて、今度は変数間の関係性や、変数と予測値との関係性をより詳細にとられるために、shap.dependence_plotを使ってみましょう。shap.dependence_plotは、y=axのグラフで、縦軸yがSHAP値、横軸xが特徴量というグラフになります。
shap.dependence_plot("Age", shap_values[1], X_test,display_features=X_test_display)
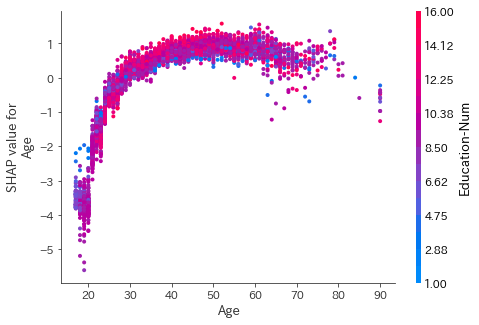
これをみると、30歳以下であることは予測に対して負方向へ大きく影響を与えていますが、40歳を超えると予測の正方向への影響が頭打ちになっていることが分かります。これは、先ほどまでの年齢が、負方向の予測に大きく影響しているという結果とも矛盾はありません。また、色分けがされている右側の変数は、交互作用が一番強い特徴量が勝手に選択されて表示されます。つまり、年齢が同じでもEducation-Numによって予測への影響力が異なっていることが見てとれます。自分で交互作用を確認したい変数を選択する、もしくは、何も指定したくない場合は以下のようにします。
#年齢と性別との交互作用 shap.dependence_plot("Age", shap_values[1], X_test,display_features=X_test_display,interaction_index="Sex") #一変数のみ選択 shap.dependence_plot("Age", shap_values[1], X_test,display_features=X_test_display,interaction_index=None)
さらに、shap.summary_plotでは確認できなかったカテゴリーごとの影響もみることができます。
shap.dependence_plot("Relationship", shap_values[1], X_test,display_features=X_test_display)
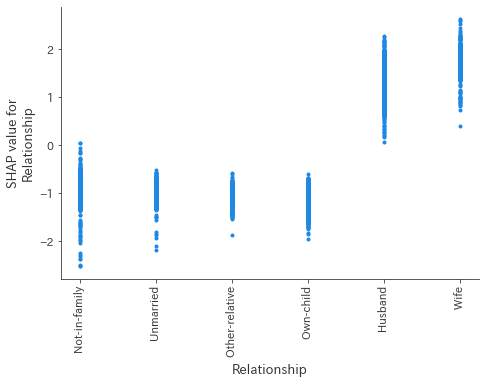
これをみると妻もしくは夫であることは、正方向の予測に寄与し、それ以外の場合は負方向へ影響していることが分かります。
shap.decision_plot
さらに踏み込んでモデルを解釈したい場合はshap.decision_plotを使ってみましょう。 shap.decision_plotは、決定木のように予測の過程を可視化することができ、主にIndividualな影響を見るために使います。
misclassified = (np.round(pred) != y_test) shap.decision_plot(explainer.expected_value[1], shap_values[1][0:20],X_test_display[0:20],link="logit",highlight=misclassified[0:20])
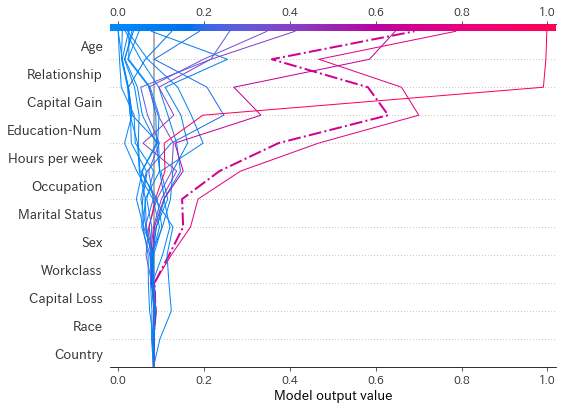
20人の予測過程を可視化してみました。highlightにindexを指定すると、点線になるので、今回は予測を間違えたサンプルをハイライトしてあります。 これをみるとどのサンプルが、どの特徴量から、どれぐらいの影響を受けて最終的な予測値になったのか一目でわかりますね。間違えて予測された1サンプルをみてみます。
#予測を間違えたサンプルのインデックスを取得する。 miss_index = np.argsort(misclassified[0:20])[::-1][0] shap.decision_plot(explainer.expected_value[1], shap_values[1][miss_index],X_test_display.iloc[miss_index,:],link="logit",highlight=0)
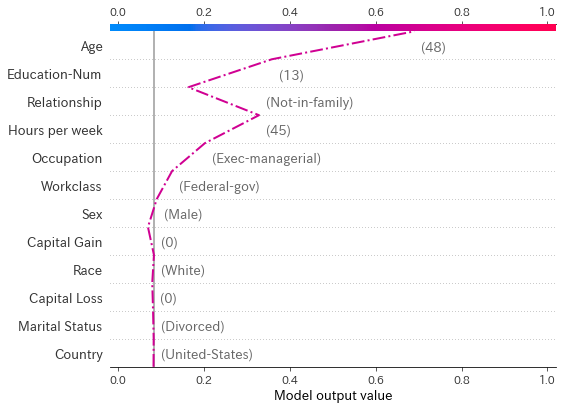
shap.decision_plotは1サンプルのみを表示させると、特徴量の値も表示されます。これをみると、このサンプルはAge48歳であることと、Educataion-Num13年であることが、大きく正方向に影響を与えているようです。
また、予測の典型的なパターンを確認することもできます。feature_order='hclust'とすると、同じような予測パターンのサンプルを近くに表示してくれます。高収入確認が99%以上と予測されたサンプルを見てみましょう。
idx = pred>=0.99 shap.decision_plot(explainer.expected_value[1], shap_values[1][idx],X_test_display[idx].iloc[:,:],link="logit",feature_order='hclust')
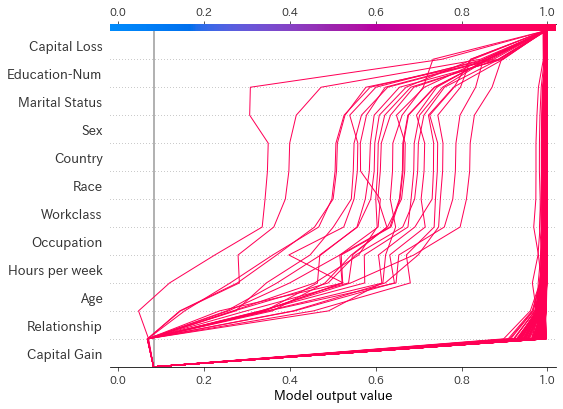
ここから、高収入であると予測されるサンプルの多くは、Capital Gainからほとんどの影響を受けるパターンと、Age,Relation Shipから影響を受けるパターンの2種類に分けられそうですね。このようにshap.decision_plotはGlobalな影響も確認することができます。
まとめ
今回は機械学習モデルを直感的に解釈するためのSHAPについてまとめました。分類問題しか扱いませんでしたが、連続量のモデルでも同様にSHAPを使うことが出来ます。特徴量の選択やエンジニアリングに対してもSHAPを使ってみると新たな視座を得ることができそうですね!
※本記事は筆者が個人的に学んだことをまとめた記事になります。所属する組織の意見・見解とは無関係です。また、数学の記法や詳細な理論、用語等で誤りがあった際はご指摘頂けると幸いです。