世の中の事象における真の因果関係は神のみぞが知り、それに抗うために多くの因果推論テクニックが作られてきました。その中でも傾向スコアというのは、ランダム化検証ができない事象でも、データをゴニョゴニョすることで、理論上ランダム化に等しいことができてしまうという夢のようなテクニックです。
今回はそんな傾向スコアが前提としている仮定や、傾向スコアを使う際の注意点、RとPython使っての解析方法などについて書いていきます。
解析方法を手っ取り早く知りたいという方は後半からご覧ください。
- 今回のデータ
- 簡単に回帰分析
- CMとプレイ時間の関係に影響を及ぼすのは?
- 全ての変数を調整することはできない
- 傾向スコアマッチング
- 傾向スコアを変数として使う
- Rでの実践
- Pythonでの実践
- まとめ
- 参考
今回のデータ
今回は岩波データサイエンスvol3のデータセットを使います。データはこちらからダウンロードできます。

- 作者: 岩波データサイエンス刊行委員会
- 出版社/メーカー: 岩波書店
- 発売日: 2016/06/10
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (4件) を見る
データはスマホゲームプレイ時間やそのゲームCMをみたかどうか、TVの視聴時間、年齢や性別、居住地などを含んでいます。 変数は以下を使います。
- CM:CMをみたかどうか
- area:居住地(ダミー変数)
- sex:性別
- marry:結婚の有無(ダミー変数)
- child:子供の有無(ダミー変数)
- job:職業(ダミー変数)
- gamesecond :ゲームのプレイ時間
- TVwatch_day:一日のTV視聴時間
- inc:所得
今回の目的はCMを見たかどうかとゲームのプレイ時間の因果関係を推論してみます。
なお、今回は成書の内容には沿わず、筆者オリジナルの解析を行っていくため、成書の内容とは異なっていることをご了承ください。
簡単に回帰分析
まずはデータの特徴を掴むため、可視化と簡単な解析を行いましょう。以下はCMの有無と平均ゲームプレイ時間のグラフです。

CMを見ていないを0、CMを見たを1とすると、CM0が3108秒、1が2478秒で、CMをみた人のほうがプレイ時間が短いという負の影響になってしまいした。
次に回帰分析を使ってCMの2群間に、ゲームプレイ時間が有意に異なっているかを調べてみます。因果推論において回帰分析を使う意味についてはこちらを
結果はこちらになります。
| term | estimate | std.error | p.value |
|---|---|---|---|
| (Intercept) | 3107.71 | 234.9 | 0.00 |
| CM1 | -629.64 | 364.8 | 0.08 |
傾きであるCM1は-630なので、CM0に比べてCM1はゲームプレイ時間が630秒短いという解釈になります。(標準誤差が大きくp値も0.08であるため、必ずしも有意な差があるとは言えませんが...)
しかし、これは単純な関係であって因果関係ではありません。さらに因果関係を探っていきましょう。
CMとプレイ時間の関係に影響を及ぼすのは?
CMを見たほうがゲームプレイ時間が短いという関係を説明するための仮説を立ててみましょう。いわゆる交絡因子です。
まずは年齢の影響が考えられますね。年齢が高い人ほどテレビをよく見るため、CMを見る可能性が高く、ゲームのプレイ時間が短いと言う仮説には違和感がありません。
CMと年齢の分布を確認してみます。以下はCM0を上向きヒストグラム、1は下向きヒストグラムに書いたものです。数字は人数を表しています。
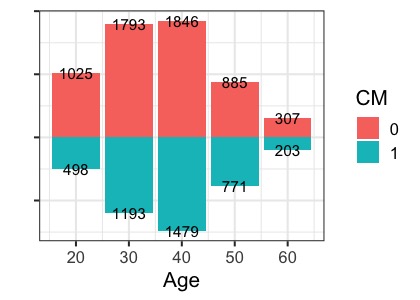
特に顕著なのは20代で、CMを見た人が圧倒的に少ないですね。
年齢は、CMとゲームプレイ時間の交絡因子となっていそうです。年齢という変数を入れて重回帰分析をしてみましょう。
結果はこちらです。
| term | estimate | std.error | p.value |
|---|---|---|---|
| (Intercept) | 7004.80 | 729.7 | 0.00 |
| CM1 | -476.42 | 365.3 | 0.19 |
| age | -96.97 | 17.2 | 0.00 |
年齢の平均因果効果である傾きは-97で、やはり年齢が高いほどゲームプレイ時間が短くなるようです。また、CMの平均因果効果も先ほどに比べて、-476秒と小さくなっています。
他に想定される仮説としては、TVの視聴時間が長い人はスマホゲームのプレイ時間が短く、CMをみる可能性が高くなるため、TVの視聴時間も交絡因子として想定されます。こちらも分布確認してみましょう。
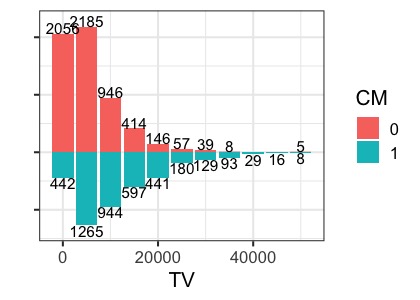
見たところ、CM0の群はテレビ視聴時間が短く、CM1は長い人が多いようです。TVの視聴時間も入れて解析を行った結果が以下になります。
| term | estimate | std.error | p.value |
|---|---|---|---|
| (Intercept) | 6980.35 | 729.9 | 0.00 |
| CM1 | -270.07 | 391.7 | 0.49 |
| age | -91.03 | 17.7 | 0.00 |
| TVwatch_day | -0.04 | 0.0 | 0.14 |
TVの視聴時間の係数はマイナスになっており、仮説を支持する結果となりました。さらにCMの係数の大きさが標準誤差よりも小さくなり、CMはプレイ時間の長さにほとんど影響を及ぼしていません。
全ての変数を調整することはできない
さて、今までみてきたようにCMとゲームプレイ時間の関係は様々な変数から交絡を受けてしまいます。つまり、CM0とCM1の間では様々な変数の分布が均等ではありません。試しに今回の変数全ての平均値の差を確認してみます。
| Diff | 95%conf | |
|---|---|---|
| gamesecond | 629.64 | (-58.9,1318.1) |
| area_kanto | -0.07 | (-0.1,-0.1) |
| area_keihan | -0.19 | (-0.2,-0.2) |
| area_tokai | 0.03 | (0.0,0.0) |
| area_keihanshin | 0.23 | (0.2,0.2) |
| job_dummy1 | 0.08 | (0.1,0.1) |
| job_dummy2 | 0.01 | (-0.0,0.0) |
| job_dummy3 | -0.02 | (-0.0,-0.0) |
| job_dummy4 | 0 | (-0.0,0.0) |
| job_dummy5 | -0.07 | (-0.1,-0.1) |
| job_dummy6 | -0.02 | (-0.0,-0.0) |
| job_dummy7 | 0.02 | (0.0,0.0) |
| job_dummy8 | 0 | (-0.0,0.0) |
| age | -1.58 | (-2.0,-1.2) |
| sex | 0.07 | (0.1,0.1) |
| marry_dummy | -0.04 | (-0.1,-0.0) |
| inc | 27.55 | (16.9,38.2) |
| pmoney | 0.01 | (-0.1,0.1) |
| child_dummy | 0 | (-0.0,0.0) |
| TVwatch_day | -5746.9 | (-6053.3,-5440.5) |
やはり多くの変数で、分布が異なっているようです。
このまま一つずつ仮説を立てて、変数を加えたり抜いたりしながら、全ての変数を調整する方法もありますが、変数が膨大になった場合はモデルとしても不安定になり、回帰分析の前提も厳しくなってしまいます。
そこで、なんとか全ての変数の分布を均等にする方法はないのかという考えのもと作られたのが、傾向スコア(Propencity Score)です。傾向スコアは、簡単にいうとCMを見るかどうかの確率(割付確率とも言います)のことを指します。傾向スコアを使った解析方法はいくつかありますが、それぞれが前提としている仮定が異なるため、注意が必要です。
今回は傾向スコアマッチングと傾向スコアをそのまま変数として使う方法の二つを紹介します。
傾向スコアマッチング
傾向スコアマッチングとは、傾向スコアが似ている人をそれぞれの群間でマッチングして、その平均値を比較しようというものです。わかりにくいので、実際にやりながら説明していきます。
まずは、データセットにある全ての変数を使って、傾向スコアを計算します。アウトカムがCM1orCM0の2値になるので、ロジスティック回帰のモデルを使いましょう。
式としてはこんな感じです。
このモデルを使って、それぞれの人がCMを見るかどうかの確率を算出して、先ほどと同様に上下のヒストグラムにしてみます。

傾向スコアの分布が異なっていますね。傾向スコアマッチングは傾向スコアが似ている人をマッチングさせていき、マッチングしない人を除くことで、この分布を均等にします。
マッチングさせる範囲はだいたい前後0.5%ぐらいが一般的です。具体的には傾向スコア65.1%の人と65.6%の人がマッチする範囲になります。
マッチング後の傾向スコアヒストグラムはこんな感じです。
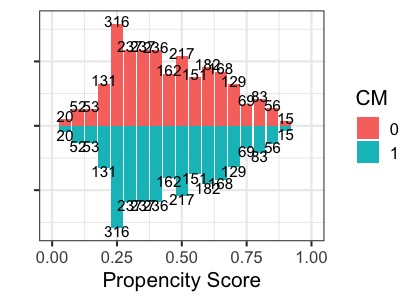
マッチング後は分布を確認
傾向スコアマッチングの注意点として、精度の高い割付確率を算出することが目的ではなく、全ての交絡因子の分布を2群の間で等しくすることが本来の目的になります。
先ほどの年齢とテレビの視聴時間の分布を確認してみましょう。
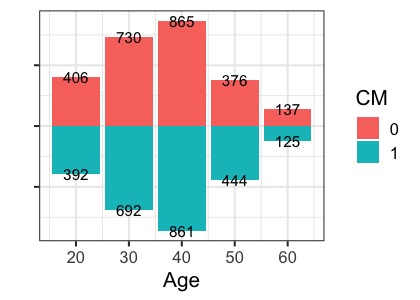
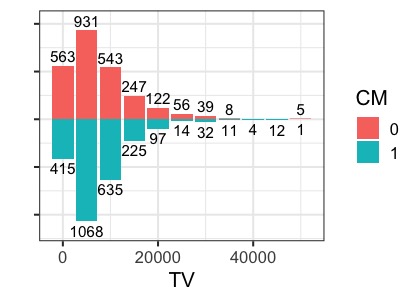
それぞれの分布は均等にばらついているように見えます。先ほどと同様にマッチング後の変数それぞれについて、2群でt検定をしてみます。
| Diff | 95%conf | |
|---|---|---|
| gamesecond | 1016.63 | (177.4,1855.9) |
| area_kanto | 0 | (-0.0,0.0) |
| area_keihan | 0.01 | (-0.0,0.0) |
| area_tokai | 0 | (-0.0,0.0) |
| area_keihanshin | -0.01 | (-0.0,0.0) |
| job_dummy1 | 0.03 | (-0.0,0.1) |
| job_dummy2 | -0.01 | (-0.0,0.0) |
| job_dummy3 | -0.01 | (-0.0,0.0) |
| job_dummy4 | 0 | (-0.0,0.0) |
| job_dummy5 | 0.01 | (-0.0,0.0) |
| job_dummy6 | -0.01 | (-0.0,0.0) |
| job_dummy7 | 0 | (-0.0,0.0) |
| job_dummy8 | -0.01 | (-0.0,0.0) |
| age | -0.41 | (-1.0,0.2) |
| sex | 0 | (-0.0,0.0) |
| marry_dummy | -0.03 | (-0.1,-0.0) |
| inc | 12.17 | (-2.6,27.0) |
| pmoney | 0.18 | (-0.0,0.4) |
| child_dummy | -0.03 | (-0.1,-0.0) |
| TVwatch_day | 8.01 | (-358.8,374.8) |
| ps | 0 | (-0.0,0.0) |
どの変数でも2群の間で平均値に差はなさそうです。
マッチングの結果は?
さて、本来の目的であるCMによるゲームプレイ時間の平均値を確認してみましょう。2つの群で交絡因子の分布が等しければ、単純に2群の平均値を比較すれば良いので、単回帰分析でやってみると
| term | estimate | std.error | p.value |
|---|---|---|---|
| (Intercept) | 2885.647 | 302.7017 | 0.0000000 |
| CM1 | -1016.627 | 428.0848 | 0.0175945 |
またまたCM1の方がゲームプレイ時間が短いという結果になりました。
傾向スコアマッチングの注意点(重要)
傾向スコアマッチングは一見ランダム化試験のように感じられ、もっともらしいように思われますが、いくつか注意点があります。
1つ目は、傾向スコアを計算するために使用する変数が、交絡因子の全てであることを前提としていることです。実は今回のデータセットには他にも多くの変数が記録されていますが、説明を簡単にするために適当に変数をピックアップしました。傾向スコアマッチングは使用した変数のみの分布しか考慮されないため、もし他に交絡因子があった場合は、その影響を考慮することはできません。今回のように交絡因子とする変数が不十分になる場合は、マッチングの仕方によって結果が大きく異なってしまいます。
2つ目は、マッチングしなかったサンプルを除くため、サンプル数が減ってしまうどころか、それ自体がバイアスになってしまうことです。 今回の場合は10000サンプル中、マッチしたのは5000強だったので、半数近くサンプルを無駄にしてしまっています。
傾向スコアマッチングは非常に使いやすく、直感的にも分かりやすいですが、結果は絶対ではなく、吟味が必要であるということを念頭に置いておきましょう。
傾向スコアを変数として使う
傾向スコアを使った解析方法の2つ目は、傾向スコア自体を変数として重回帰分析に入れることです。実際にやってみると以下のようになります。
| term | estimate | std.error | p.value |
|---|---|---|---|
| (Intercept) | 3534.274 | 346.2874 | 0.0000000 |
| CM1 | -273.926 | 422.0331 | 0.5163127 |
| ps | -1385.077 | 826.3673 | 0.0937491 |
今回の結果からもCM1の方がゲームプレイ時間が短いという結果になりましたが、前回も書いた通り、回帰分析では全ての傾向スコア間で要因とアウトカムとの関係が等しいことを前提としています。
試しに傾向スコアを0から1まで、10分類してそれぞれの分類で、CM間のゲームプレイ時間の平均値を比較してみると
| PS | Diff | 95%Conf |
|---|---|---|
| 0.2 | 430 | (-2129,2989 ) |
| 0.3 | -289 | (-1335,757 ) |
| 0.4 | -3337 | (-4675,-1999 ) |
| 0.5 | 6669 | (4354,8984 ) |
| 0.6 | 2734 | (1611,3857 ) |
| 0.7 | 1888 | (-518,4295 ) |
| 0.8 | -4574 | (-6972,-2176 ) |
| 0.9 | -2165 | (-3153,-1176 ) |
傾向スコアのグループごとでゲームプレイ時間の平均値の差が異なっていることが分かりますね。回帰分析の前提が成り立っていないため、結果の解釈には注意が必要です。
また、傾向スコアを回帰分析に変数として入れるのは本来の使い方ではないという意見もあります。どんな解析にも言えることですが、全ての解析手法は絶対ではなく、どんな制約があり、どんな仮定を置いているのかをしっかりと確認しなければいけませんね。
Rでの実践
さて、理論的なところはこの辺で、Rで実際に傾向スコアを使ってみましょう。なお、解析コードを見やすくするため、グラフの可視化コードは最小限に抑えてあります。
まずは、データを読み込んで、使用する変数を選択します。
library(tidyverse) dat <- read_csv("q_data_x.csv") dat <- dat %>% rename(CM=cm_dummy) %>% mutate(CM=as.character(CM), sex=as.character(sex)) %>% select(CM,gamesecond,matches("area"),matches("job"),age,sex,marry_dummy,inc,pmoney,child_dummy,TVwatch_day)
続いて年齢とテレビ視聴時間の変数を入れて、回帰分析をします。tidy{broom}は解析結果を見やすくまとめてくれます。
#CMのみ dat %>% lm(data=.,gamesecond~CM) %>% broom::tidy() # A tibble: 2 x 5 term estimate std.error statistic p.value <chr> <dbl> <dbl> <dbl> <dbl> 1 (Intercept) 3108. 235. 13.2 1.22e-39 2 CM1 -630. 365. -1.73 8.44e- 2 #年齢を追加 dat %>% lm(data=.,gamesecond~CM+age) %>% broom::tidy() # A tibble: 3 x 5 term estimate std.error statistic p.value <chr> <dbl> <dbl> <dbl> <dbl> 1 (Intercept) 7005. 730. 9.60 9.97e-22 2 CM1 -476. 365. -1.30 1.92e- 1 3 age -97.0 17.2 -5.64 1.75e- 8 #テレビ視聴時間を追加 dat %>% lm(data=.,gamesecond~CM+age+TVwatch_day) %>% broom::tidy() # A tibble: 4 x 5 term estimate std.error statistic p.value <chr> <dbl> <dbl> <dbl> <dbl> 1 (Intercept) 6980. 730. 9.56 1.40e-21 2 CM1 -270. 392. -0.690 4.90e- 1 3 age -91.0 17.7 -5.15 2.63e- 7 4 TVwatch_day -0.0375 0.0257 -1.46 1.44e- 1
続いて今回の変数について、平均値を比較しましょう。map{purrr}を使って全ての変数でt検定を行います。
ttest <- map_dfr(dat[,-1],function(col){ #t検定の結果を格納 res <- t.test(data=dat,as.numeric(col)~CM) c(round(res$estimate[1]-res$estimate[2],2),sprintf("(%.1f,%.1f)",res$conf.int[1],res$conf.int[2])) } ) %>% t() #転置する colnames(ttest) <- c("Diff","95%conf") > ttest Diff 95%conf gamesecond "629.64" "(-58.9,1318.1)" area_kanto "-0.07" "(-0.1,-0.1)" area_keihan "-0.19" "(-0.2,-0.2)" area_tokai "0.03" "(0.0,0.0)" area_keihanshin "0.23" "(0.2,0.2)" job_dummy1 "0.08" "(0.1,0.1)" job_dummy2 "0.01" "(-0.0,0.0)" job_dummy3 "-0.02" "(-0.0,-0.0)" job_dummy4 "0" "(-0.0,0.0)" job_dummy5 "-0.07" "(-0.1,-0.1)" job_dummy6 "-0.02" "(-0.0,-0.0)" job_dummy7 "0.02" "(0.0,0.0)" job_dummy8 "0" "(-0.0,0.0)" age "-1.58" "(-2.0,-1.2)" sex "0.07" "(0.1,0.1)" marry_dummy "-0.04" "(-0.1,-0.0)" inc "27.55" "(16.9,38.2)" pmoney "0.01" "(-0.1,0.1)" child_dummy "0" "(-0.0,0.0)" TVwatch_day "-5746.9" "(-6053.3,-5440.5)"
ここからロジスティック回帰分析を使って傾向スコアを計算していきます。
#ロジスティック回帰を使う ps_fit <- glm(as.numeric(CM) ~area_keihan+area_tokai+area_keihanshin+age+I(age*age)+sex+marry_dummy+job_dummy2+job_dummy3+job_dummy4+job_dummy5+job_dummy6+job_dummy7+job_dummy8+inc+I(inc*inc)+pmoney+I(pmoney*pmoney)+child_dummy+TVwatch_day+I(TVwatch_day*TVwatch_day),family = binomial(),data=dat) #predictを使って確率を計算 ps<- predict(ps_fit,type="response",newdata = dat) #データフレームに傾向スコアを格納 dat <- dat %>% mutate(ps=ps) #データの可視化 dat %>% mutate(ps = round(ps/0.05)*0.05) %>% group_by(CM) %>% count(ps) %>% mutate(n2 = ifelse(CM==0,n,-n)) %>% ggplot(aes(x=ps,y=n2,fill=CM))+ geom_bar(stat = "identity")+ labs(x="Propencity Score",y=" ")+ theme(axis.text.y = element_blank())+ geom_text(aes(x=ps, y=n2+ifelse(CM==0,10,-10),label=n))
まず一行目では、glmを使ってロジスティック回帰を行います。変数にはデータセット全ての変数を使いますが、ダミー変数はひとつ抜くことと、連続量は二乗の項も入れていることに注意してください。
これは人によるかと思いますが、二乗の項を加えることでモデルが柔軟になるため、筆者は入れることにしています。詳しくは参考文献(ハーバード)をご参照ください。
続いてpredictを使って確率を計算しています。こうすることで、変数に欠損があり、モデル作成に使用されなかった人のデータも計算することができます。
いよいよマッチングを行います。Rには{Maching}というパッケージがありますが、今回はマッチングのイメージを分かりやすくするため、for文で記載しました。パッケージとはマッチングアルゴリズムが異なるため、結果が多少異なりますがご了承ください。
#マッチングの範囲を指定 inter <- seq(0,1,0.005) #マッチング後のデータを入れるためのからデータフレーム dat_match <- tibble() for(i in inter){ match0 <- dat %>% filter(CM=="0",ps<=i,ps>i-0.005) match1 <- dat %>% filter(CM=="1",ps<=i,ps>i-0.005) #一つ目の条件で、CM0とCM1のどちらか一方が0人の場合を除外する。 if(nrow(match0)!=0 && nrow(match1)!=0){ #二つ目の条件で人数が少ない方に合わせてランダムにマッチングする if(nrow(match0)<nrow(match1)){ match1 <- match1 %>% slice(sample(seq(1,nrow(match1)),size=nrow(match0))) dat_match <- bind_rows(dat_match,match1,match0) }else{ match0 <- match0 %>% slice(sample(seq(1,nrow(match0)),size=nrow(match1))) dat_match <- bind_rows(dat_match,match1,match0) } } }
マッチングが終わったら、データの分布確認と平均値の比較をします。
dat_match %>% mutate(ps = round(ps/0.05)*0.05) %>% group_by(CM) %>% count(ps) %>% mutate(n2 = ifelse(CM==0,n,-n)) %>% ggplot(aes(x=ps,y=n2,fill=CM))+ geom_bar(stat = "identity")+ labs(x="Propencity Score",y=" ")+ theme(axis.text.y = element_blank())+ geom_text(aes(x=ps, y=n2+ifelse(CM==0,10,-10),label=n))+ coord_cartesian(xlim=c(0,1)) #平均値の比較 ttest <- map_dfr(dat_match[,-1],function(col){ #t検定の結果を格納 res <- t.test(data=dat_match,as.numeric(col)~CM) c(round(res$estimate[1]-res$estimate[2],2),sprintf("(%.1f,%.1f)",res$conf.int[1],res$conf.int[2])) } ) %>% t() #転置する colnames(ttest) <- c("Diff","95%conf") > ttest Diff 95%conf gamesecond "1016.63" "(177.4,1855.9)" area_kanto "0" "(-0.0,0.0)" area_keihan "0.01" "(-0.0,0.0)" area_tokai "0" "(-0.0,0.0)" area_keihanshin "-0.01" "(-0.0,0.0)" job_dummy1 "0.03" "(-0.0,0.1)" job_dummy2 "-0.01" "(-0.0,0.0)" job_dummy3 "-0.01" "(-0.0,0.0)" job_dummy4 "0" "(-0.0,0.0)" job_dummy5 "0.01" "(-0.0,0.0)" job_dummy6 "-0.01" "(-0.0,0.0)" job_dummy7 "0" "(-0.0,0.0)" job_dummy8 "-0.01" "(-0.0,0.0)" age "-0.41" "(-1.0,0.2)" sex "0" "(-0.0,0.0)" marry_dummy "-0.03" "(-0.1,-0.0)" inc "12.17" "(-2.6,27.0)" pmoney "0.18" "(-0.0,0.4)" child_dummy "-0.03" "(-0.1,-0.0)" TVwatch_day "8.01" "(-358.8,374.8)" ps "0" "(-0.0,0.0)"
マッチング後のデータを使って、ゲームプレイ時間とCMとの関係を単回帰を使って解析します。
dat_match %>% lm(dat=.,gamesecond~CM) %>% broom::tidy() # A tibble: 2 x 5 term estimate std.error statistic p.value <chr> <dbl> <dbl> <dbl> <dbl> 1 (Intercept) 2886. 303. 9.53 2.31e-21 2 CM1 -1017. 428. -2.37 1.76e- 2
続いて、傾向スコアを変数に入れて回帰分析を行います。これは簡単ですね。
dat %>% lm(data=.,gamesecond~CM+ps) %>% broom::tidy() # A tibble: 3 x 5 term estimate std.error statistic p.value <chr> <dbl> <dbl> <dbl> <dbl> 1 (Intercept) 3534. 346. 10.2 2.45e-24 2 CM1 -274. 422. -0.649 5.16e- 1 3 ps -1385. 826. -1.68 9.37e- 2
最後に傾向スコアをグループにして、それぞれのグループごとでゲーム時間の平均値を比較してみます。
#psグループを作る dat <- dat %>% mutate(ps_gp = round(ps/0.1)) #結果の入れものを作る ps_dat <- as.tibble(matrix(numeric(8*3),ncol=3)) i <- 1 for (deciles in c(2:9)) { res <- t.test(gamesecond~CM, data=dat[dat$ps_gp==deciles,]) ps_dat[i,] <- c(deciles*0.1, round(res$estimate[1]-res$estimate[2]), sprintf("(%.0f,%.0f )",res$conf.int[1],res$conf.int[2])) i <- i + 1 } colnames(ps_dat) <- c("PS","Diff","95%Conf") > ps_dat # A tibble: 8 x 3 PS Diff `95%Conf` <chr> <chr> <chr> 1 0.2 430 (-2129,2989 ) 2 0.3 -289 (-1335,757 ) 3 0.4 -3337 (-4675,-1999 ) 4 0.5 6669 (4354,8984 ) 5 0.6 2734 (1611,3857 ) 6 0.7 1888 (-518,4295 ) 7 0.8 -4574 (-6972,-2176 ) 8 0.9 -2165 (-3153,-1176 )
Pythonでの実践
本記事のグラフや解析はRを使った結果になりますが、Pythonでも傾向スコアマッチングを行うことができます。なお、解析コードを見やすくするため、グラフの可視化コードは最小限に抑えてあります。
まずは、データを読み込んで、使用する変数を選択します。
import numpy as np import pandas as pd import statsmodels.api as sm import matplotlib.pyplot as plt from scipy import stats import random from dfply import * %matplotlib inline dat = pd.read_csv("q_data_x.csv") dat = dat>>rename(CM="cm_dummy")>>select(X.CM,X.gamesecond,matches("area"),matches("job"),X.age,X.sex,X.marry_dummy,X.inc,X.pmoney,X.child_dummy,X.TVwatch_day)
続いて年齢とテレビ視聴時間の変数を入れて、回帰分析をします。
##CMのみ ols = sm.OLS.from_formula("gamesecond~CM",data=dat) res = ols.fit() res.summary().tables[1]
#年齢を追加 ols = sm.OLS.from_formula("gamesecond~CM+age",data=dat) res = ols.fit() res.summary().tables[1]
#テレビ視聴時間を追加 ols = sm.OLS.from_formula("gamesecond~CM+TVwatch_day",data=dat) res = ols.fit() res.summary().tables[1]
続いて、今回の変数について平均値を比較しましょう。ループで全ての変数に対してt検定を行い、分布を確認します。
dat0 = dat.query("CM==0") dat1 = dat.query("CM==1") #dat.query("CM==0") #dat[dat.CM==1] for i in range(1,len(dat.columns)): res = stats.ttest_ind(dat0.iloc[:,i],dat1.iloc[:,i]) diff = mean(dat0.iloc[:,i])-mean(dat1.iloc[:,i]) col = dat0.columns[i] print(" {:} {:5.1f} (p: {:1.3f})".format(col,diff,res.pvalue))
ここからロジスティック回帰分析を使った傾向スコアを計算していきます。
#傾向スコアを計算 formula = ( "CM ~area_keihan+area_tokai+area_keihanshin+age+I(age*age)" "+sex+marry_dummy+job_dummy2+job_dummy3+job_dummy4+job_dummy5+job_dummy6+job_dummy7+job_dummy8" "+inc+I(inc*inc)+pmoney+I(pmoney*pmoney)+child_dummy+TVwatch_day+I(TVwatch_day*TVwatch_day)" ) model = sm.Logit.from_formula(formula, data=dat) res = model.fit() dat["ps"] = res.predict(dat) #可視化 propensity0 = dat.ps[dat.CM==0] propensity1 = dat.ps[dat.CM==1] bins = np.arange(0, 1, 0.05) top0, _ = np.histogram(propensity0, bins=bins) top1, _ = np.histogram(propensity1, bins=bins) plt.ylim(-1000,1000) plt.axhline(0, c='black') plt.bar(bins[:-1]+ 0.025, top0, width=0.04, facecolor='red') plt.bar(bins[:-1]+ 0.025, -top1, width=0.04, facecolor='blue') plt.axhline(0, c='black') for x, y in zip(bins, top0): plt.text(x + 0.025, y + 10, str(y), ha='center', va='bottom') for x, y in zip(bins, top1): plt.text(x + 0.025, -y - 10, str(y), ha='center', va='top')
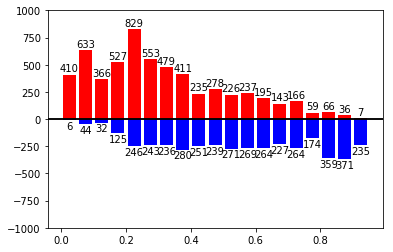
まずは、ロジスティック回帰を行います。変数にはデータセット全ての変数を使いますが、ダミー変数はひとつ抜くことと、連続量は二乗の項も入れていることに注意してください。
これは人によるかと思いますが、二乗の項を加えることでモデルが柔軟になるため、筆者は入れることにしています。詳しくは参考文献(ハーバード)をご参照ください。
続いてpredictを使って確率を計算し、データに格納しました。こうすることで、変数に欠損があり、モデル作成に使用されなかった人のデータも計算することができます。
最後は可視化用のコードです。
いよいよマッチングを行います。Pythonには傾向スコアマッチングのパッケージはないので自作しました。本来のマッチングアルゴリズムとは異なることをご了承ください。
#マッチングの範囲を指定 inter = np.arange(0,1,0.005) #マッチング後のデータを入れるためのからデータフレーム dat_match=pd.DataFrame() #一つ目の条件で、CM0とCM1のどちらか一方が0人の場合を除外する。 for i in inter: match0 = dat[(dat.CM==0) &(i-0.005 < dat.ps)& (dat.ps<i)] match1 = dat[(dat.CM==1) &(i-0.005 < dat.ps)& (dat.ps<i)] #二つ目の条件で人数が少ない方に合わせてランダムにマッチングする if (match0.shape[0]!=0)&(match1.shape[0]!=0): if match0.shape[0]<=match1.shape[0]: match1= match1.iloc[random.sample(range(0,match1.shape[0]),match0.shape[0]),:] dat_match = pd.concat([dat_match,match0,match1]) else : match0= match0.iloc[random.sample(range(0,match0.shape[0]),match1.shape[0]),:] dat_match = pd.concat([dat_match,match0,match1])
マッチングが終わったら、先ほど同様に平均値の比較をします。
dat0 = dat_match.query("CM==0") dat1 = dat_match.query("CM==1") for i in range(1,len(dat.columns)): res = stats.ttest_ind(dat0.iloc[:,i],dat1.iloc[:,i]) diff = mean(dat0.iloc[:,i])-mean(dat1.iloc[:,i]) col = dat0.columns[i] print(" {:} {:5.1f} (p: {:1.3f})".format(col,diff,res.pvalue))
マッチング結果を先ほど同様にグラフにする。
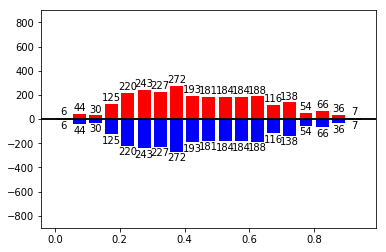
続いて、傾向スコアを変数に入れて回帰分析を行います。これは簡単ですね。
ols = sm.OLS.from_formula("gamesecond~CM",data=dat_match) res = ols.fit() res.summary().tables[1]
最後に傾向スコアをグループにして、それぞれのグループごとでゲーム時間の平均値を比較してみます。
dat["ps_gp"] = round(dat.ps/0.1) dat0 = dat.query("CM==0") dat1 = dat.query("CM==1") for i in range(2,10): res = stats.ttest_ind(dat0.gamesecond[dat0.ps_gp==i],dat1.gamesecond[dat1.ps_gp==i]) diff = mean(dat0.gamesecond[dat0.ps_gp==i])-mean(dat1.gamesecond[dat1.ps_gp==i]) col = "ps"+str(i) print(" {:} {:5.1f} (p: {:1.3f})".format(col,diff,res.pvalue))
まとめ
今回は因果推論でよく使われる傾向スコアの使い方について書いてきました。傾向スコアはとても便利な理論ですが、使い方や解釈の吟味はしっかり行いましょう。
傾向スコアのその他の解析手法としては、IPWがありますが、こちらは今回とは全く解釈の異なる解析手法になるので、また次回まとめていきます。
Pythonは慣れていないので、コードが汚いかもしれません.... もっとスマートな書き方があれば、ご教授ください。
※本記事は筆者が個人的に学んだことをまとめた記事なります。数学の記法や詳細な理論、筆者の勘違い等で誤りがあった際はご指摘頂けると幸いです。
参考
今回のデータはこちらの書籍のものになります。傾向スコアやIPWなど因果推論に関する基本的なスキルはこれ一冊で事足りるのでは?と思うぐらいまとまっております。

- 作者: 岩波データサイエンス刊行委員会
- 出版社/メーカー: 岩波書店
- 発売日: 2016/06/10
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (4件) を見る
理論的な背景までしっかりとまとまっていますので、詳しい理論が知りたい方にはオススメです。

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)
- 作者: 星野崇宏
- 出版社/メーカー: 岩波書店
- 発売日: 2009/07/29
- メディア: 単行本
- 購入: 29人 クリック: 285回
- この商品を含むブログ (26件) を見る
ハバード大学が無料で公開している因果推論に関するテキストです。RやPythonのコードもあり、これが無料で読めるとは本当にすごいです。本記事の内容もこちらを参考にしています。
https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/
因果推論に関して、おそらく日本で一分かりやすく、しかも丁寧に解説されているブログです。大変参考にさせて頂いてます。
データから因果関係をどう導く?:統計的因果推論の基本、「反事実モデル」をゼロから - Unboundedly
Pythonの傾向スコアマッチングについてはこちらを参考にさせて頂きました。
Pythonで傾向スコア(Propensity score)マッチングとIPWを実装してみた - Np-Urのデータ分析教室