前回は因果推論の王道テクニックである傾向スコアを使った回帰分析とマッチングについて紹介しました。今回も傾向スコアを使った解析手法の一つであるIPWと、傾向スコアは使いませんが理論的には同じになるStandardzationの紹介をしていきます。
この二つのモデルは、今まで扱ってきたモデルとは少し違い集団全体の因果効果(Marginal effect)を推定するモデルになります。集団全体の因果効果であるため、交絡因子の層ごとに要因の結果の関係性が異なっていたとしても、効果を推定することができます。
具体的な解析手法のみが気になる方は後半にRとPythonコードをのせてありますので、そちらをご参照ください。
そもそも因果推論ってなんぞ?って方はこちら
- Marginal effectとConditionnal effect
- 今回のデータ
- Conditional effect
- Marginal effect
- 傾向スコアを使ったIPWの実践
- Rでの実践
- Pythonでの実戦
- まとめ
- 参考
Marginal effectとConditionnal effect
今までの回帰分析は、条件付きの平均値を求めることと同等で、これをConditional effectと呼びます。
しかし、前回から書いているように、Conditional effectによる集団全体の推定値は、全ての条件間で要因と結果との関連が等しいことを条件としているため、現実ではかなり厳しい前提になります。
そこで、条件間で要因と結果との関連が等しくない場合に、集団全体の因果効果を推定するためのテクニックとして、IPWやStandaridizationがあり、これらのモデルで推定された平均因果効果をMariginal effectと呼びます。
この二つはあまり意識されることはありませんが、とても重要な違いになります。実際に解析を通してイメージを掴んでいきます。
今回のデータ
今回は岩波データサイエンスvol3のデータセットを使います。データはこちらからダウンロードできます。

- 作者: 岩波データサイエンス刊行委員会
- 出版社/メーカー: 岩波書店
- 発売日: 2016/06/10
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (4件) を見る
データはスマホゲームプレイ時間やそのゲームCMをみたかどうか、TVの視聴時間、年齢や性別、居住地などを含んでいます。 変数は以下を使います。
- CM:CMをみたかどうか(1:みた 0:みてない)
- area:居住地(ダミー変数)
- sex:性別
- marry:結婚の有無(ダミー変数)
- child:子供の有無(ダミー変数)
- job:職業(ダミー変数)
- gamesecond :ゲームのプレイ時間
- TVwatch_day:一日のTV視聴時間
- inc:所得
今回の目的はCMを見たかどうかとゲームのプレイ時間の因果関係を推論してみます。
なお、今回は成書の内容には沿わず、筆者オリジナルの解析を行っていくため、成書の内容とは異なっていることをご了承ください。
Conditional effect
まずはConditional effectですが、回帰分析で求めることができます。回帰分析については以前の記事でしっかりまとめてありますので、ご参考にしてみてください。
さて、年齢、性別、子どもの有無、TV視聴時間を変数に入れて重回帰分析でCMとゲームプレイ時間の関連を解析してみましょう。結果はこうなります。
| term | estimate | std.error | p.value |
|---|---|---|---|
| (Intercept) | 5905.03 | 761.5 | 0.00 |
| CM1 | -116.23 | 391.8 | 0.77 |
| age | -110.89 | 17.9 | 0.00 |
| sex1 | 2367.76 | 381.8 | 0.00 |
| child_dummy1 | 551.08 | 363.9 | 0.13 |
| TVwatch_day | -0.03 | 0.0 | 0.27 |
この結果から、"交絡因子を除いた場合のCMの効果は-116である”、つまり、CMをみた方がゲームのプレイ時間が116秒短くなるという解釈になりそうですが、厳密にはそうではありません。
厳密には、"もし性別、年齢、子供の有無、テレビの視聴時間が同じ人たちで比べた時、CMの効果は平均的に-116である"となります。
つまり
- 性別が男で、年齢が30歳で、子供がいて、テレビの視聴時間が6000秒で、CMをみた人
- 性別が男で、年齢が30歳で、子供がいて、テレビの視聴時間が6000秒で、CMをみていない人
を比べた時にゲームのプレイ時間は116秒違うし、
- 性別が女で、年齢が50歳で、子供がいなくて、テレビの視聴時間が3600秒で、CMをみた人
- 性別が女で、年齢が50歳で、子供がいなくて、テレビの視聴時間が3600秒で、、CMをみていない人
を比べた時もゲームのプレイ時間は116秒違う
という解釈になり、その他全ての条件を変えても、CMの効果は116秒であるという前提を置いています。これがConditional effectです。
しかし、実際に私たちが知りたいのは、もしターゲット全体がCMをみたらゲームプレイ時間はどれぐらい異なるのかということだと思います。これはまさに集団全体への効果"Marginal effect"で、IPWやStandardizationというテクニックで求めることができます。
Marginal effect
Standardization
Marginal effectは少しイメージしにくいですが、一番分かりやすいものとしてはそれぞれの条件で、要因と結果との関連を重み付け平均することです。
例えば男女によるCMとゲープレイ時間の関係を考えてみます。まずは、CM1、CM0の男女による平均値の違いをみてみましょう。
| sex | CM0 | CM1 | CM_diff |
|---|---|---|---|
| 0 | 1731 | 1458 | -273 |
| 1 | 3782 | 3167 | -615 |
男性(1)の方がゲームプレイ時間は長いようですね。また、女性でのCM効果は-273、男性では-615です。ここからMariginal effectを求めてみます。
Mariginal effectは集団全体に対するCMの効果なので、純粋な平均ではなく、男女の比率で加重平均値を計算します。男女の人数は以下になります。
| sex | n |
|---|---|
| 0 | 3597 |
| 1 | 6403 |
これで性別の加重平均を計算すると
となるので、これがMariginal effectになり、もし男女関係なく無作為にCMをみるかみないかが決まる場合、CMがゲームプレイ時間に与える影響は-492秒であると言えます。
これがStandardizationという手法です。式で表すと
となります。ややこしいですが、それぞれで層別化した平均因果効果をその層に含まれる確率をかけて求めています。
しかしこれはあまり実用的ではありません。なぜなら変数が多くなった場合、もしくは0or1のように2値ではない場合は、層別化することができなくなるからです。
そこで、IPW(Inverse Probably Weight)という傾向スコアから計算される確率で重み付けをする手法を使ってMarginal effectを求めていきます。
IPW(Inverse Probably Weight)
さて、Marginal effectを求める際によく用いられるのがIPW(Inverse Probably Weight)です。IPWは少し混みいった理論になるのですが、直感的な理解としてはこうです。
Marigina effectは集団全体へ介入した時の効果である。(今回はCMをみた時の効果)
しかし、観察データでは介入条件の群と非介入条件の群では、背景因子に偏りがある。(男性の方がCMを見る人が少ないなど)
その偏りが2群の間で全て同じになれば、単純に平均値を比較するだけで集団全体の効果を推定できる。
その偏りを同じにするために、各個人を仮想的に増やして均等にする。
どれぐらい増やすかは介入、非介入に割り当てられる確率で決めよう。
という理論です。もう少し具体的に行きます。まずは話を簡単にするため、変数には性別のみを考えCM0、CM1の男女の分布を見てみます。
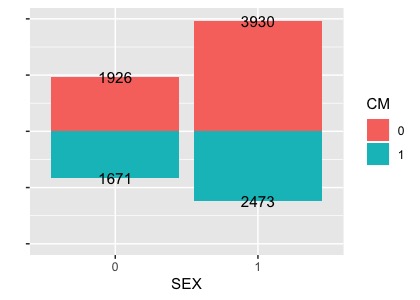
sex=1が男性ですが、見た所男性の方がCMをみていない割合が多そうです。ゲームプレイ時間は男性の方が長いので、性別は交絡因子となります。
ここからMariginal effectを求めていきます。まずは、CM1or0になる確率を求めます。ここで注意点ですが傾向スコアはCM1になる確率でした。しかし、IPWで使われる確率はCM1or0になる確率です。つまり、その人が受けた条件となる確率とも言えます。
ややこしいですが、とりあえずは納得して頂いて実際に求めてみます。
| sex | CM0 | CM1 |
|---|---|---|
| 0 | 0.535 | 0.465 |
| 1 | 0.614 | 0.386 |
ここから、女性だった場合にCMを見る確率は46.5%、見ない確率は53.5%、男性も同様に...です。この確率の逆数を重みとして、
| sex | CM0 | CM1 |
|---|---|---|
| 0 | 1.87 | 2.15 |
| 1 | 1.63 | 2.59 |
CMを見た女性は2.15倍、見ていない女性は1.87倍に、男性も同様にすると、男女の人数の分布は以下のようになります。

何と、男女の分布が同じになりました。このようにして、各サンプルに重みをつけて分布を同じにする手法がIPWです。人数を増やすと言うのは直感的な理解で、実際に求める際は重み付け最小二乗法で求めます。IPWを使ってCMの効果を求めてみましょう。
| term | estimate | std.error | p.value |
|---|---|---|---|
| (Intercept) | 3044.51 | 249.7 | 0.00 |
| CM1 | -492.07 | 353.1 | 0.16 |
CMの効果は-492と、Standardizationで求めた結果と同じになりました。
補足:StandardizationとIPWの違い
実はIPWとStandardizationは同じ理論で成り立っており、パラメトリックなモデルを仮定しなかった場合は、この二つは同じ結果になります。また、ブートストラップの手法を使えば、連続量や多変量でもStandardizationを使ってMrginal effectを推定できます。
しかし、何らかのモデルを仮定して仮にモデルが不十分であった場合は、それぞれが異なる結果となります。これはStandardizationとIPWがモデルを作る際に何をアウトカムとするのかに起因し、Standardizationでは推定したい結果(今回はゲームプレイ時間)をモデルのアウトカムとするのに対して、IPWでは傾向スコアを求める際に要因側(今回はCM)をアウトカムにします。
これ以上はあまり詳しく書きませんが、この違いによって結果が異なってしまい、もしStandardizationとIPWで結果が大きく異なる場合はモデルが不十分である可能性があるとだけ覚えておきましょう。
さらに詳しく知りたい方は参考文献(ハーバード)をご参照ください。
傾向スコアを使ったIPWの実践
さて、調整したい分布は性別だけではありません。年齢、テレビの視聴時間、子供の有無...などなどCM0とCM1を純粋に比較するために分布を同じにしたい変数はたくさんあります。
そこで、先ほどは性別だけを変数としましたが、今度は調整したい全ての変数を使って傾向スコアを求めてみましょう。
使用する変数は上述した変数を使用します。傾向スコアからそれぞれの介入条件に割り当てられる確率を求め、その逆数からIPWを計算します。
適当に選んだ5人の結果をみてみましょう。
| CM | ps | p | ipw |
|---|---|---|---|
| 0 | 0.22 | 0.78 | 1.28 |
| 1 | 0.50 | 0.50 | 2.01 |
| 0 | 0.18 | 0.82 | 1.23 |
| 1 | 0.28 | 0.28 | 3.54 |
| 0 | 0.39 | 0.61 | 1.63 |
左からCMの変数、傾向スコア(ps)、介入条件に割り当てられる確率(p)、その逆数(ipw)となっています。
そしてこのipwで重み付けをしてゲームプレイ時間に対するCMの効果を推定してみます。
| term | estimate | std.error | p.value |
|---|---|---|---|
| (Intercept) | 2877.3152 | 249.0607 | 0.0000000 |
| CM1 | 230.3633 | 354.3203 | 0.5156068 |
この結果から、もし無作為にCMをみるかみないかが決まる場合、集団全体のCMがゲームプレイ時間に与える影響は230秒であると言え、これがまさに知りたかった値、Mariginal effectですね。
IPWはこのようにして集団全体へ介入をした場合の効果を推定することができます。
補足:岩波データサイエンスとの用語対応
ここで、本記事で参考にさせて頂いている成書と、使用している用語が多少異なりますので、整理しておきます。
まず、介入群と非介入群の差である平均処置効果(Average Treatment Effect:ATE)と書かれている用語に対応するのが、先ほどから求めいるMariginal effectの値になります。しかし、Conditional effectも一種のATEであるため、本記事では用語をMariginal effectに統一しました。
また、介入群における平均介入効果(Average Treatment Effect on the Treated: ATT)は、本記事では紹介していませんが、一般的にはSMRW(standardized-mortality-ratio weights)などと言われる手法を使います。名前は違えど、傾向スコアを使って重みをつけるという考え方に違いはありません。イメージとしては、IPWが全体を仮想的に増加させるのに対して、SMRWは、介入群はそのままで、非介入群のみ介入群と分布が同じになるように増加させます。結果の解釈としては、"介入群が受けた介入の効果"となります。ちなみに傾向スコアマッチングの推定値もATTに近くなります。
これらの手法の違いについては、参考文献(論文)をご参照ください。
Rでの実践
ここからRでIPWを実践していきます。傾向スコアを求めるところまでは前回と同じですので、コードのみを記載しています。
#データの読み込みと変数の選択 library(tidyverse) dat <- read_csv("q_data_x.csv") dat <- dat %>% rename(CM=cm_dummy) %>% mutate(CM=as.character(CM), sex=as.character(sex) , child_dummy = as.character(child_dummy)) %>% dplyr::select(CM,gamesecond,matches("area"),matches("job"),age,sex,marry_dummy,inc,pmoney,child_dummy,TVwatch_day) #ロジスティック回帰を使う ps_fit <- glm(as.numeric(CM) ~area_keihan+area_tokai+area_keihanshin+age+I(age*age)+sex+marry_dummy+job_dummy2+job_dummy3+job_dummy4+job_dummy5+job_dummy6+job_dummy7+job_dummy8+inc+I(inc*inc)+pmoney+I(pmoney*pmoney)+child_dummy+TVwatch_day+I(TVwatch_day*TVwatch_day),family = binomial(),data=dat) #predictを使って確率を計算 ps<- predict(ps_fit,type="response",newdata = dat)
さて、ここで求めた傾向スコアを使って介入条件に割り当てられる確率(p)、その逆数(ipw)を計算します。
dat <- dat %>% mutate(ps = ps, #傾向スコア p = ifelse(CM==0,1-ps,ps), #CMが0だったら1-傾向スコアを計算 ipw = 1/p)#逆数にする
ipwが計算できたらあとはglm{stats}の引数weightにipwを指定して、回帰分析を行うだけです。
dat %>% glm(data=.,gamesecond~CM,weights = ipw) %>% broom::tidy() # A tibble: 2 x 5 term estimate std.error statistic p.value <chr> <dbl> <dbl> <dbl> <dbl> 1 (Intercept) 2877. 249. 11.6 1.12e-30 2 CM1 230. 354. 0.650 5.16e- 1
うまく計算できました。ただし本文では触れていませんでしたが、標準誤差が大きいため、今回の結果ではCMがゲームプレイ時間に与える影響はほとんどない可能性もあることに注意しましょう。
Pythonでの実戦
ここからはPythonでもIPWを実践してみましょう。傾向スコアを求めるところまでは前回と同じですので、コードのみを記載しています。
#データの読み込みと変数の選択 import numpy as np import pandas as pd import statsmodels.api as sm from dfply import * dat = pd.read_csv("q_data_x.csv") dat = dat>>rename(CM="cm_dummy")>>select(X.CM,X.gamesecond,matches("area"),matches("job"),X.age,X.sex,X.marry_dummy,X.inc,X.pmoney,X.child_dummy,X.TVwatch_day) formula = ( "CM ~area_keihan+area_tokai+area_keihanshin+age+I(age*age)" "+sex+marry_dummy+job_dummy2+job_dummy3+job_dummy4+job_dummy5+job_dummy6+job_dummy7+job_dummy8" "+inc+I(inc*inc)+pmoney+I(pmoney*pmoney)+child_dummy+TVwatch_day+I(TVwatch_day*TVwatch_day)" ) model = sm.Logit.from_formula(formula, data=dat) res = model.fit() ps = res.predict(dat)
さて、ここで求めた傾向スコアを使って介入条件となる確率(p)、その逆数(ipw)を計算します。
ps = res.predict(dat) p = np.zeros(dat.shape[0]) p[dat["CM"]==0] = 1-ps[dat["CM"]==0] p[dat["CM"]==1] = ps[dat["CM"]==1] ipw= 1/p
最後にstatsmodelsのWLSを使って重み付きの推定値を求めます。
wls = sm.WLS.from_formula("gamesecond~CM", weights=ipw,data=dat) res = wls.fit() res.summary().tables[1]
| coef | std err | t | P>|t| | |
|---|---|---|---|---|
| Intercept | 2877.3152 | 249.061 | 11.553 | 0.000 |
| CM | 230.3633 | 354.320 | 0.650 | 0.516 |
うまくいきました!ただし本文では触れていませんでしたが、標準誤差が大きいため、今回の結果ではCMがゲームプレイ時間に与える影響はほとんどない可能性もあることに注意しましょう。
まとめ
全2回に分けて、傾向スコアを使った解析手法を紹介してきました。強調しておきたいのは、どのモデルが一番正しいということはなく、検証したい仮説とデータの背景からどの解析手法を使うのか適切なのかを選択しなければならないと言うことです。
傾向スコアは因果推論においてはかなり重宝するテクニックですので、結果の解釈やモデルの使い方はしっかりと確認しておきたいですね。
※本記事は筆者が個人的に学んだことをまとめた記事なります。数学の記法や詳細な理論、用語等で誤りがあった際はご指摘頂けると幸いです。
参考
今回のデータはこちらの書籍のものになります。傾向スコアやIPWなど因果推論に関する基本的なスキルはこれ一冊で事足りるのでは?と思うぐらいまとまっております。

- 作者: 岩波データサイエンス刊行委員会
- 出版社/メーカー: 岩波書店
- 発売日: 2016/06/10
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (4件) を見る
ピンク本と呼ばれるこちらの書籍、理論的な背景までしっかりとまとまっていますので、詳しい理論が知りたい方にはオススメです。

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)
- 作者: 星野崇宏
- 出版社/メーカー: 岩波書店
- 発売日: 2009/07/29
- メディア: 単行本
- 購入: 29人 クリック: 285回
- この商品を含むブログ (26件) を見る
ハバード大学が無料で公開している因果推論に関するテキストです。RやPythonのコードもあり、これが無料で読めるとは本当にすごいです。本記事の内容もこちらを参考にしています。
https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/
因果推論に関して、おそらく日本で一分かりやすく、しかも丁寧に解説されているブログです。大変参考にさせて頂いてます。
データから因果関係をどう導く?:統計的因果推論の基本、「反事実モデル」をゼロから - Unboundedly
因果推論手法の比較を行なっている論文です。それぞれのモデルに必要な前提条件や結果の解釈など、勉強になります。
傾向スコアを使った解析手法の特徴がグラフィカルに書かれており、とても参考になるスライドです。本記事を書く上で、一番参考にさせて頂きました。