リンゴで理解する尤度とは~離散確率から正規分布まで~ - 医療職からデータサイエンティストへ

統計学を学んでいておそらくつまずくであろう尤度。こいつの正体をリンゴを使ってまとめていきます。

尤度とは？

尤度の何が難しいかと言うとまずはこの漢字。そもそも何と読むかと言うと"ゆうど"と読みます。”尤”なんて日常生活でまず使うことはありません。何でわざわざこんなに難しい漢字を使うんだと初めは愚痴をこぼしたくなりますがそこは我慢します。

尤度の求め方

さて、漢字の読み方が分かったところでこの"ゆうど"とは何かと言うと、どれぐらい起こりやすいかを表す指標になります。例えば以下のような問題を考えてみます。

図のようにA,B,Cの文字が書いてあるリンゴが箱の中に入っています。それぞれ何個ずつ入っているかは分かりませんが全部で30こあることは分かっています。この箱からリンゴを10個取り出した時、Aリンゴが2個、Bのリンゴが5個、Cのリンゴが3個でした。この箱の中には各番号のリンゴがどれぐらいの個数ずつ入っていると考えるのが良いでしょうか？

ここで、素直にリンゴは平等に10こずつ入っていると仮定した場合に、今回の比率でリンゴを選ぶ確率は、30 こから10こ選び、その中にAが2こある確率、Bが5こある確率、Cが3こある確率を掛け合わせれば求まるので、
$\dfrac{{}_{10} C _{2}\,{}_{10} C _{5}\,{}_{10} C _{3}}{{}_{30} C _{10}}$
となり、これを計算すると

> choose(10,2)*choose(10,5)*choose(10,3)/choose(30,10)
[1] 0.04529204

およそ4パーセントぐらいになりました。つまり、リンゴを10こ選んだ時、この問題のようなリンゴの個数になる起こりやすさは4パーセント言うことになります。これを尤度と呼びます。

尤度は起こりやすさを表しているので、確率も尤度の一種と言えるでしょう。

尤度の最大化

さて、尤度は何となく理解したところでA,B,Cそれぞれ入っているリンゴの個数を変化させ、尤度が大きくなるところを探せばこの問題が解けそうです。

例えば、取り出したリンゴの状況から、A,Cは少なそうなので5こずつぐらい、Bは一番多そうなので20こぐらい入っていると仮定すると
$\dfrac{{}_{5} C _{2}\,{}_{20} C _{5}\,{}_{5} C _{3}}{{}_{30} C _{10}}$

> choose(5,2)*choose(20,5)*choose(5,3)/choose(30,10)
[1] 0.05160257

起こりやすさが5パーセントと確率が上がりました。こうやって計算していくと...

> choose(6,2)*choose(15,5)*choose(9,3)/choose(30,10)
[1] 0.125937

Aのリンゴが6こ、Bのリンゴが15こ、Cのリンゴが3この時が一番尤度が高く12パーセントになり、これが答えになります。この個数をどうやって求めたかと言うと
$Aのリンゴ\, :\, \dfrac{2}{10}\times30 = 6　\\ Bのリンゴ\, : \,\dfrac{5}{10}\times30 = 15 \\ Cのリンゴ\, : \,\dfrac{3}{10}\times30 = 9$
と求めました。実は10こ選んだリンゴの割合と同じ時に尤度が最大になることが分かっています。これが尤度と尤度の最大化（最尤法）になります。

確率密度の尤度

さて、尤度とは何かをふわっと理解したところで、この尤度の最大化の真骨頂である確率密度関数へ発展させていきたいと思います。

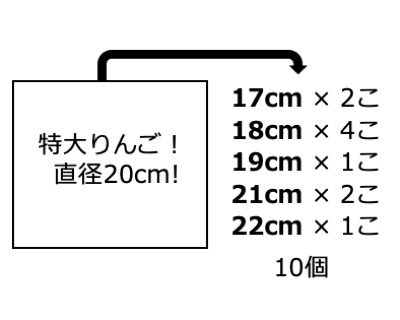
箱の中にたくさんのリンゴが入っています。この箱には”特大リンゴ！直径20cm！”と書かれています。この箱からリンゴを10こ取り出して直径を測ったところ以下の図のようになりました。この箱のリンゴの直径は何センチと考えるのが良いでしょうか？

先ほどと同じように10こ取り出した時に問題のようなリンゴが取り出される起こりさすさを計算すれば良さそうです。しかし、先ほどと違うのはリンゴの直径は連続値であることです。

例えば今回のリンゴの直径は整数になっていますが、おそらくベテランのリンゴ師（？）が測定すると18.43cmとなり、さらに精密な電子測定器を使えば18.4343....とぴったり18cmになるリンゴはこの世には存在しないことになります。

確率密度関数

連続値になった場合、その値になる確率が0パーセントになるので尤度計算に必要な確率を求めることができません。そこで登場するのが確率密度関数です！詳しい説明はこちらの記事が分かりやすいかと思います！
11-4. 確率密度と確率密度関数 | 統計学の時間 | 統計WEB
確率密度は確率ではなく、相対的な起こりやすさだと思ってください。今回は箱に直径20cmと書かれているので、リンゴの直径は平均20cmの正規分布に従うと仮定しましょう。 f:id:h-wadsworth02:20181224121523p:plain
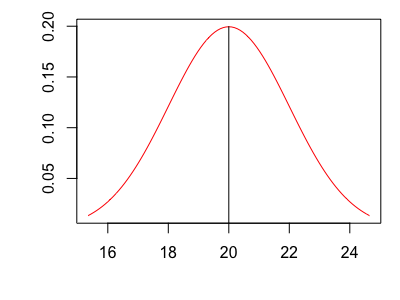
このグラフの高さが起こりやすさを表しており、直径を測った際に20cmになることが一番起こりやすく、15cmや25cmなどになることは稀にしか起こらないことを表しています。この正規分布の確率密度関数は
$f(x)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(x-\mu)^{2} }{ 2\sigma^{2}}\right\}$
で表されます。それぞれの確率密度を求めると...

> apple <- c(17,17,18,18,18,18,19,21,21,22)
> round(dnorm(apple,20,2),2)
 [1] 0.06 0.06 0.12 0.12 0.12 0.12 0.18 0.18 0.18 0.12

出ました!今回は標準偏差 $\sigma$ を2と仮定しました。17,22cmが0.06、18cmが0.12、19,21cmが0.18となり、グラフとも一致しています。これは確率ではなく、相対的な起こりやすさを表す値であることに注意してください。

ここから尤度を求めるには全て掛け合わせます。すると
$(0.06\times2)\times(0.12\times4)\times\cdots\times(0.12\times1) = 6\times10^{-10}$
となります。とても小さな値に見えますが、確率ではなく相対的な起こりやすさを表しているため、他と比べてみないと分かりません！

そこで、仮定する正規分布の平均を17cm~22cmまでを0.1cmずつ変化させ、求めた尤度をプロットしてみると
f:id:h-wadsworth02:20181224121812p:plain

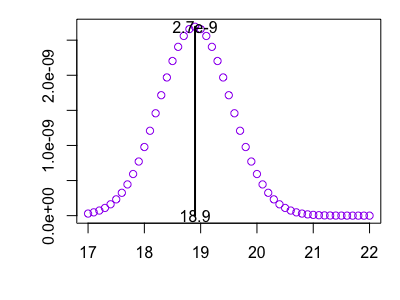
18.9cmの時に尤度が最大になることが分かりました！箱の文言は過剰評価していると考えた方が良さようです。

実はこの18.9cmと言うのは取り出した10この平均値でもあります！先ほどと同様にサンプルの平均値が尤度最大になりました！

尤度最大化さらに詳しく！

ここからは尤度の最大化について、数式で見てみましょう！ここから先は少し難しくなるので、ざっくりと理解したい方は読み飛ばしてください。
まず、正規分布の確率密度関数は

$f(x)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(x-\mu)^{2} }{ 2\sigma^{2}}\right\}$

と表せました。ここから、先ほどの例で尤度を考えてみると

$P(x_{1},x_{2},x_{3}\cdots,x_{10}) \\ = \dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(17-\mu)^{2} }{ 2\sigma^{2}}\right\}\times\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(17-\mu)^{2} }{ 2\sigma^{2}}\right\}\\ \times\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(18-\mu)^{2} }{ 2\sigma^{2}}\right\}\cdots\times\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(20-\mu)^{2} }{ 2\sigma^{2}}\right\}\\ = \prod_{i = 1}^{10}\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(x_{i}-\mu)^{2} }{ 2\sigma^{2}}\right\}$

と表せます！この $\small\prod$ は総積で、総和 $\sum$ の掛け算バージョンになります。つまり、それぞれの確率密度を掛け合わせた $\small\prod_{i = 1}^{10}\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(x_{i}-\mu)^{2} }{ 2\sigma^{2}}\right\}$ を最大化するような $\mu$ を求めればよさそうです。

関数の最大化には"微分"を使うのが定石で、微分を簡単にするために対数変換をすると言うのが数学のお作法のようです。（高校の頃から数学嫌いだった私は、そのお作法に慣れるまで愚痴をこぼし続けました。）

さて、お作法にしたがって自然対数変換(底がe)してみると

$\log {\prod_{i = 1}^{10}\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(x_{i}-\mu)^{2} }{ 2\sigma^{2}}\right\}} \\ = \sum_{i = 1}^{10}\log {\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(x_{i}-\mu)^{2} }{ 2\sigma^{2}}\right\}}\\ =\sum_{i=1}^{10}(\log \dfrac{1}{\sqrt{2\pi}\sigma} + \log \exp\left\{-\dfrac{(x_{i}-\mu)^{2} }{ 2\sigma^{2}}\right\})\\ =\dfrac{10}{2}\log (2\pi\sigma^{2})-\dfrac{1}{2\sigma^{2}}\sum_{i=1}^{10}(x_{i}-\mu)^{2}$

さらにこの式を $\mu$ で偏微分すると

$\dfrac{\partial}{\partial \mu}\dfrac{10}{2}\log (2\pi\sigma^{2})-\dfrac{1}{2\sigma^{2}}\sum_{i=1}^{10}(x_{i}-\mu)^{2} \\ = \dfrac{1}{\sigma^{2}}\sum_{i=1}^{10}(x_{i}-\mu)$
となりこれが0になるところが最大になるので（傾きが0で最大になります）...
$\mu = \dfrac{x_{1}+x_{2}+ \cdots+x_{10}}{10}$
結局平均値の時に尤度が最大になることが分かります！