第1回：RとPythonで学ぶデータサイエンス数学~平均・分散を文字で表す~

統計学や機械学習を知る上で必ず必要になるのが算数・数学の知識です。しかし、中学や高校で数学を習ってはいるものの、いざ学び始めてみると数式や記号に圧倒されてしまう人も多いのではないでしょうか？？

今回から複数記事にまたがり、統計学や機械学習を学ぶ上で必要となる数学についてPythonとRを使い、手を動かしながら学べるような記事を書いていきます。

第一回目となる本記事では、一番の基本となる平均や分散の算出方法と数式を文字で表すことについてです。本記事の目標は2つです。

平均を $E(x) = \dfrac{1}{n}\sum_{i=1}^{n} x_{i}=\sum_{i=1}^{n} x_{i}p(x_{i})$ で表すことができる。
分散を $V(x) = \dfrac{1}{n}\sum_{i=1}^{n}(x_{i}-E(x))^{2} =(E(x^{2}))-E(x)^{2}$ で表すことができる。

これをみて、すでに吐き気がする方もひとつずつ順を追って説明していきますので、ご安心ください。誰が読んでも理解できることを目指していますので、分かりにくい、理解できない等ありましたら、お気軽にコメント頂けると幸いです。

なお、RやPythonを使わなくても、学ぶことができる内容ですので、数学の知識だけ学びたいという方も是非ご覧ください（^^）

平均を文字で表す
期待値ってなんだっけ？
平均から期待値へ
分散を文字で表す
まとめ
参考

本記事は以下の書籍を参考にしています。

データサイエンスのための数学 (データサイエンス入門シリーズ)

作者:椎名洋,姫野哲人,保科架風
発売日: 2019/08/31
メディア: 単行本（ソフトカバー）

統計学が最強の学問である[数学編]――データ分析と機械学習のための新しい教科書

作者:西内啓
発売日: 2017/12/21
メディア: 単行本（ソフトカバー）

平均を文字で表す

平均と分散を考えるにあたり、よくあるテストの点数の例題を用いて考えてみます。これはある高校のAクラスのテストの点数一覧です。

$48点\,,53点\,,66点\,,48点\,,53点\,,32点$

まずはこのAクラスの平均点を求めてみます。これは簡単ですね。

$=\dfrac{1}{6}(48+53+66+48+53+32) \\=50$

#テストの点数
test <- c(48,53, 66, 48, 53, 32)

(48+53+66+48+53+32)/6
>50
#もしくは
mean(test)
>50

import numpy as np

#テストの点数
test = np.array([48,53, 66, 48, 53,32])

(48+53+66+48+53+32)/6
>50.0
#もしくは
np.mean(test)
>50.0

さて、ここで数式を文字で表すことに慣れていきましょう。このクラスは出席番号は1~6の6人とします。このクラスの人数をnとします。このnをみたら頭の中で6と置き換えてください。次に出席番号をiとします。例えば、i=4と書いてあれば、出席番号4番の生徒を表します。そして、テストの点数はxとしましょう。例えば $x_{i=4}$ をみたら、出席番号4番の生徒のテストの点数を表すことになります。

データサイエンス数学

ここで、平均値を算出するための式を文字を使って書き直してみます。

$\dfrac{1}{n}(x_{i=1}+x_{i=2}+x_{i=3}+x_{i=4}+x_{i=5}+x_{i=6})$

どうでしょう？先程の式と見比べて見ればそれほど難しくないと思います。さらに、新たな文字を使って式を書き直してみます。

$\dfrac{1}{n}(x_{i=1}+x_{i=2}+x_{i=3}+x_{i=4}+x_{i=5}+x_{i=6}) \\= \dfrac{1}{n}\sum_{i=1}^{6} x_{i}$

この $\sum_{i=1}^{10}$ は" $x_{i=1}$ から $x_{i=6}$ までをすべて足せ"という意味の数学記号です。その値を $\dfrac{1}{n}$ しているので、平均値の式ですね。

データサイエンス数学

期待値ってなんだっけ？

さて、次は平均がE(x)を表される由縁についてご説明しましょう。E(x)のEはExpectのE、つまり期待を表し、E(x)はxの期待値という意味です。ここで期待値について復習しておきます。期待値はおそらく中学校ぐらいで習うかと思いますが、例えばこんな問題があります。

サイコロを振ってでた目が1か6であれば、500円、それ以外であれば100円が貰えるというゲームがあります。このゲームの参加費がいくらであれば、参加したいと思いますか？

このゲームに参加するに当たり、平均的に貰えるであろう金額が期待値です。今回の場合の期待値は、 $金額 \times 確率$ を全ての金額で求め、それを足し合わせることで計算されます。サイコロを振って1か6が出る確率は、 $\dfrac{2}{6}$ で、それ以外の目が出る確率は $\dfrac{4}{6}$ となります。すると貰える金額の期待値は、

$\dfrac{2}{6}\times 500+\dfrac{4}{6}\times100 = 233.33....$

500*(2/6)+100*(4/6)
>233.3333

となります。つまり、このゲームでは平均的に233円貰えることが期待されるので、参加費が233円以下であればこのゲームに参加することで得をする可能性が高いことになります。さて、ここでも期待値の式を文字に置き換えてみましょう。まず、貰える金額をxとし、xが出る確率をProbabilityのPを取って、p(x)とします。また、貰える金額500円、100円に番号をつけ、それぞれ1、2とします。例えば、 $x_{1}$ とあれば500円、 $p(x_{2})$ とあれば100円が出る確率ですので、 $\dfrac{4}{6}$ となります。これらを使って、期待値の式を置き換えてみましょう。

$\dfrac{2}{6}\times 500+\dfrac{4}{6}\times100 \\= p(x_{1})\times x_{1}+p(x_{2})\times x_{2}\\ = \sum_{i=1}^{2}x_{i}p(x_{i})$

データサイエンス数学

どうでしょう？先ほどまでのことを使えばそこまで難しくないと思います。

平均から期待値へ

さて、平均値の話をしていて、なんで期待値が出てくるの？と思った方、実は平均値と期待値とはとても関係が深い、いや、平均値と期待値は同じ概念なのです。最初のテストの話に戻りましょう。このテストの平均値問題を、

このテストで平均的に期待される点数は何点なのか？

という問題に置き換えてみます。今回、生徒は6人ですので、それぞれの点数が出る確率は $p(x_{1}),p(x_{2})\dots p(x_{6}) =\dfrac{1}{6}$ です。とするとこのテストの点数の期待値は、

$48\dfrac{1}{6}+53\dfrac{1}{6}+66\dfrac{1}{6}+48\dfrac{1}{6}+53\dfrac{1}{6}+32\dfrac{1}{6} \\=\sum_{i=1}^{6} x_{i}p(x_{i})$

と期待値の式を同じ形で表すことができます。実は、平均値とは出る値の期待値のことだったのです。

さて、これで平均値を $E(x) = \dfrac{1}{n}\sum_{i=1}^{n} x_{i}=\sum_{i=1}^{n} x_{i}p(x_{i})$ と表すことができるようになりました。平均値は期待値と同じであるという考え方は、今後、統計や機械学習を学ぶ上でとても重要になるので、しっかりおさえておきましょう！

分散を文字で表す

お次は分散についてご説明していきます。分散とはずばり、データのバラツキの平均値のことです。例えば下の図をご覧ください。どちらも平均点が50点の集団を表していますが、各個人で見てみると上の集団では、ほとんどの人が平均点の周りに集まっているのに対して、下の集団では、0〜100点までの間で、散らばっています。この散らばり具合を表すのが、分散になります。

データサイエンス数学

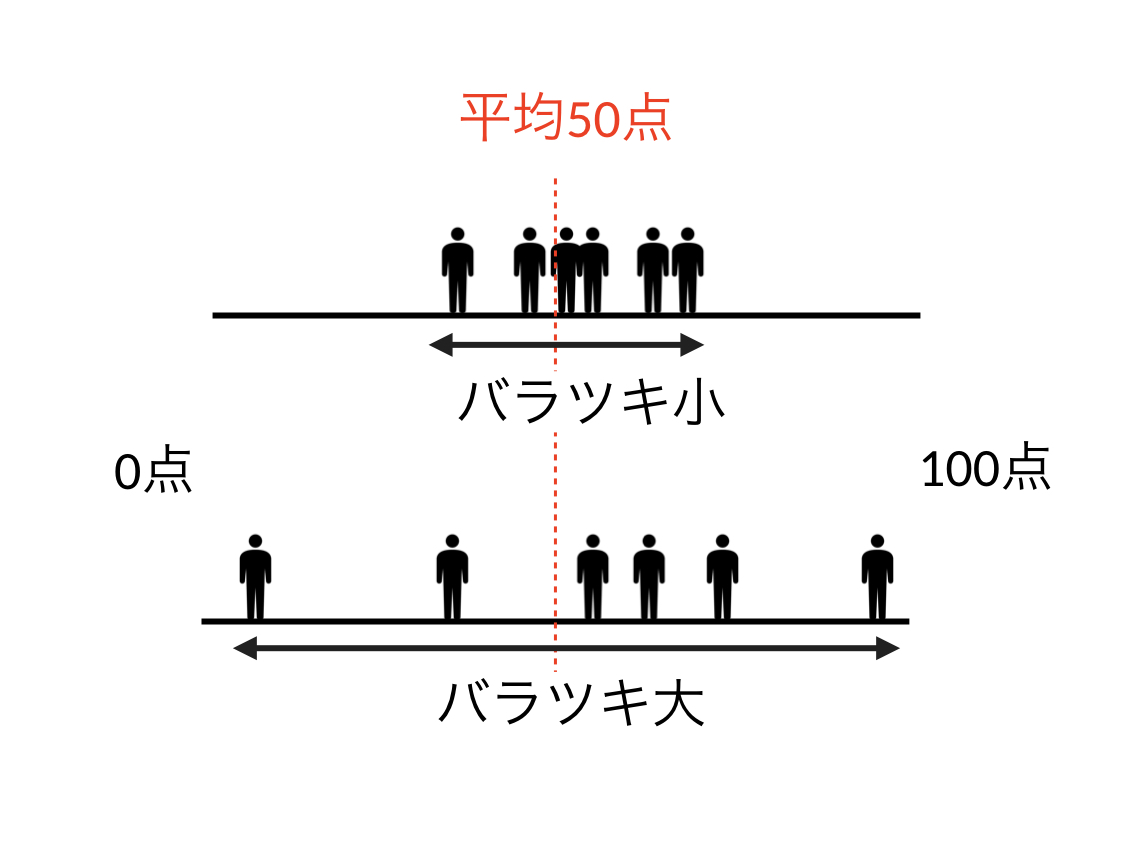
分散は平均値だけでは分からないデータのバラツキ具合を表すのに最適な指標となっています。では、この散らばり具合はどのように数値にしましょうか？分散は平均値から遠いところにいる人が多いほど（つまり、バラツキが大きいほど）値が大きくなる指標ですので、まずは各個人の点数から平均値を引き算します。イメージは以下の図のような感じです。

データサイエンス数学

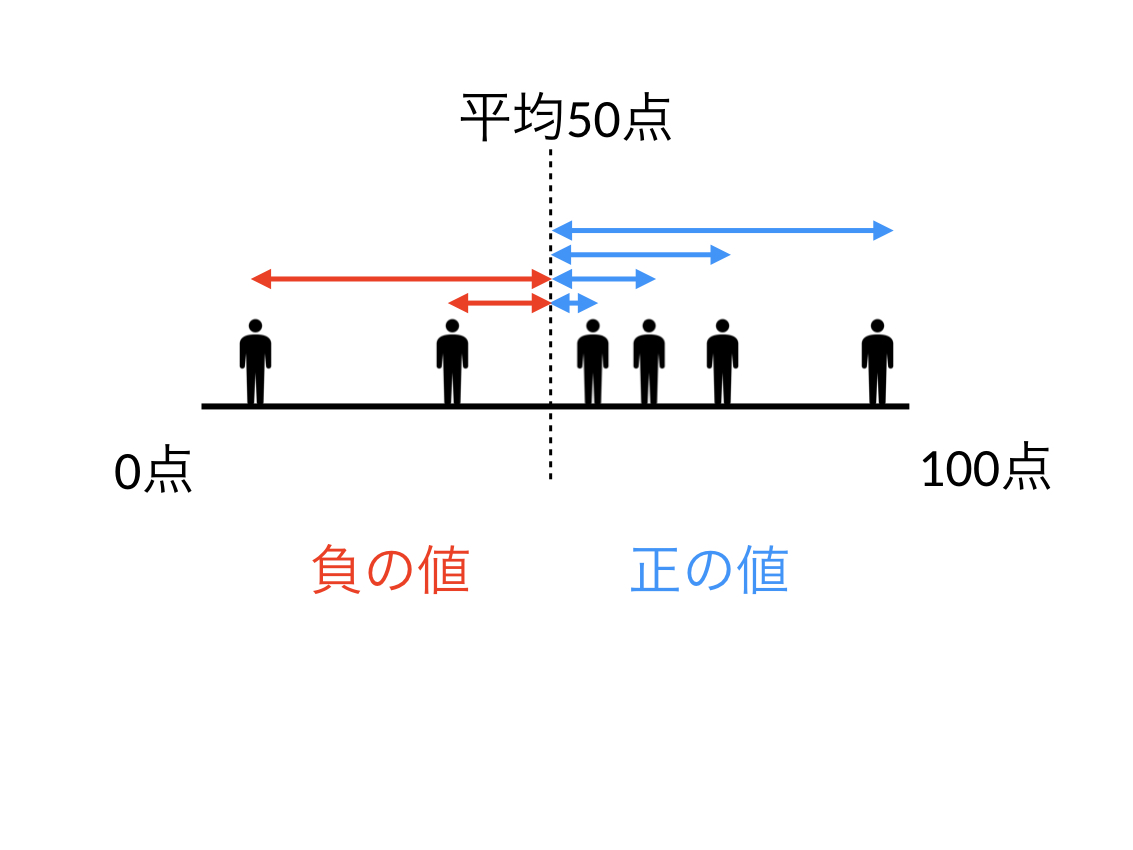
そして、この矢印が長い人が多ければバラツキが大きいことを表すので、これを足し合わせれば良さそうですが、点数から平均値を引いているので、平均値より右側の0~50点の間にいる人はマイナスの値となり、単純に足し合わせてしまうとプラスとマイナスで値を打ち消しあってしまいます。

そこで、値の2乗を足し合わせることにします。（絶対値でも良さそうですが、２乗にすることで何かと便利なことが多いので、数学のお作法だと思って勘弁しましょう。）せっかくですので、文字を使ってみましょう。点数は $x$ 、平均値はE(x)=50、各個人はi=1~6、全人数は $n=6$ です。

$(48-50)^{2}+(53-50)^{2}+(66-50)^{2}+(48-50)^{2}+(53-50)^{2}+(32-50)^{2} \\=606$

$(x_{1}-E(x))^{2}+(x_{2}-E(x))^{2}+(x_{3}-E(x))^{2}+(x_{4}-E(x))^{2}+(x_{5}-E(x))^{2}+(x_{6}-E(x))^{2} \\=\sum_{i=1}^{6}(x_{i}-E(x))^{2} \\=606$

(48-50)^2+(53-50)^2+(66-50)^2+(48-50)^2+(53-50)^2+(32-50)^2
>606
#もしくは
sum((test-mean(test))^2)

(48-50)^2+(53-50)^2+(66-50)^2+(48-50)^2+(53-50)^2+(32-50)^2
>606
#もしくは
np.sum((test-np.mean(test))**2)

ちなみにこの2乗して足した値を平方和と呼びます。分散とはバラツキの平均値ですので、6で割って平均にします。そして分散は英語でVarianceなので、そのVを取って、点数xの分散をV(x)と表せば、

$V(x) = \dfrac{1}{6}\sum_{i=1}^{6}(x_{i}-E(x))^{2} \\= 606/6 \\=101$

と表すことができます。ここまでで、分散の基本的な理解は十分ですが、さらに踏み込んで、平均値は期待値と同義であることを先ほどご説明しました。分散はバラツキの平均値ですので、 $(x-E(x))^ {2}$ の期待値であるとも言えます。つまり、

$V(x) = E( (x-E(x))^{2} )$

と書くこともできます。これを展開していくと

$V(x) = E(x^{2}- 2 x E(x) + E(x)^{2}) \\=E(x^{2}) - E(2 x E(x))+E(E(x)^{2}) \\=E(x^{2}) - 2E(x) E(x)+E(x)^{2} \\= E(x^{2}) - E(x)^{2}$

となり、xの２乗の平均値から、平均値の2乗を引いた値が、分散になることを表しています。上記の展開は分かりにくいかもしれませんが、定数の期待値はその定数の値となる（例えば6の期待値E(6)は6となる。）ことを利用し、E(x)は定数ですので、E(E(x))=E(x)であることが理解できれば、そこまで難しくない式展開です。少しずつ文字で数式を書くことに慣れていきましょう。

実際にやってみます。

$E(x^{2}) - E(x)^{2} \\= \dfrac{1}{6}(48^{2}+53^{2}+66^{2}+48^{2}+53^{2}+32^{2})-50^{2} \\=101$