前回は階層性のあるデータに対して、線形混合モデルと階層ベイズを用いて解析を行いました。
今回は、より複雑な階層ベイズモデルに挑戦していきます。前回は扱わなった、新たなデータに対しての予測も行っていきましょう。
今回のお題
前回は、生徒50人のテストの点数と勉強時間のデータを用いて、4つの学校ごとに切片と傾きが異なる(点数と勉強時間の関係性が異なる)データを解析しました。
今回は、3つの都道府県から18の学校を抽出し、そこから生徒450人をサンプリングした仮想データを用います。以下はサンプル抽出のイメージ図です。

つまり、都道県ごと、そして学校ごとでも切片と傾きが異なることを想定しています。
まずは以下を実行してデータセット(st_df)を作成し、グラフ化してみましょう。
library(ggplot2) library(dplyr) set.seed(1234) X <- rnorm(450,40,10) N_pre <- c(200,150,100) N_st1 <- c(rep(30,5),20,20,10) N_st2 <- c(30,30,20,20,20,20,10) N_st3 <- c(50,30,20) N_st <- c(N_st1,N_st2,N_st3) pref <- rep(1:3,times=N_pre) school <- rep(1:length(N_st), times=N_st) a0 <- 50 b0 <- 20 a_pre <- rnorm(3, mean=a0, sd=100) b_pre <- rnorm(3, mean=b0, sd=10) a <- rnorm(length(N_st), mean=rep(a_pre,c(8,7,3)), sd=50) b <- rnorm(length(N_st), mean=rep(b_pre,c(8,7,3)), sd=5) data_frame(X=X,school = as.factor(school),pref = as.factor(pref), a=a[school],b=b[school]) %>% mutate(Y=rnorm(450,a+b*X,30)) %>% select(X,pref,school,Y)-> st_df > st_df %>% head() # A tibble: 6 x 4 X pref school Y <dbl> <fct> <fct> <dbl> 1 27.9 1 1 519. 2 42.8 1 1 633. 3 50.8 1 1 779. 4 16.5 1 1 271. 5 44.3 1 1 776. 6 45.1 1 1 736. # グラフ化 #都道府県ごと st_df %>% ggplot(aes(x=X,y=Y,col=pref))+ geom_point(alpha = 0.5)+ geom_smooth(method = "lm",se=F) #都道府県1の学校ごと st_df %>% filter(pref=="1") %>% ggplot(aes(x=X,y=Y,col=school))+ geom_point()+ geom_smooth(method = "lm",se=F)
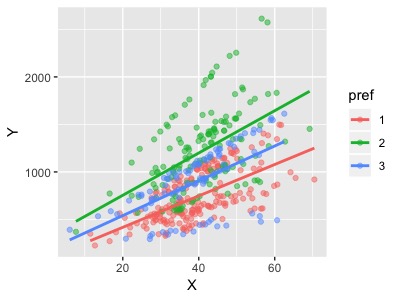

上が都道府県ごとのグラフ、下が都道府県1の学校ごとのグラフです。ご覧の通り、都道府県ごと、学校ごとで切片と傾きが異なっているようです。
このようにデータの関係性が複雑になってしまうと、前回の線形混合モデルでも扱うことはできなくなります。
しかし、こんなデータでも解析することができます。そう、階層ベイズならね。
階層ベイズの概略
まずは、いつも通り概略から行きましょう。2層の階層ベイズでは、学校ごとに異なる切片と傾きは、全体に共通の回帰直線の周りで確率的に変動する値として推定しました。

今回は、学校ごとの回帰直線を都道府県の回帰直線の周りで確率的に変動する値として、都道府県ごとの回帰直線を全体に共通の回帰直線の周りで変動する値として推定します。(ややこしい....)
イメージとしては、まず都道府県ごとの回帰直線が、全体に共通の回帰直線の周りで変動する値として推定されます。

そして、学校ごと回帰直線が都道府県ごとの回帰直線の周りで確率的に変動する値として推定されるという順番です。

ベイズ式とモデル式は以下のようになります。

上記をstanでモデリングしていきます。
階層ベイズの実践
data{ int N;//生徒数 int P;//都道府県数 int K;//学校数 real X[N];//勉強時間 real Y[N]; //点数 int<lower=1,upper=K> school[N]; int<lower=1,upper=P> pref[K]; } parameters{ real a0;//切片の全体平均 real b0;//傾きの全体平均 real ap[P];//都道府県Pの切片 real bp[P];//都道府県Pの傾き real a[K];//学校Kの切片 real b[K];//学校Kの傾き real <lower=0> sig_ap;//都道府県切片のバラツキ real <lower=0> sig_bp;//都道府県傾きのバラツキ real <lower=0> sig_a;//切片のバラツキ real <lower=0> sig_b;//傾きのバラツキ real <lower=0> sig_st;//個人差のバラツキ } model{ //超事前分布のモデル for(p in 1:P){ ap[p] ~ normal(a0,sig_ap); bp[p] ~ normal(b0,sig_bp); } for(k in 1:K){ a[k] ~ normal(ap[pref[k]],sig_a); b[k] ~ normal(bp[pref[k]],sig_b); } //事前分布のモデル for(n in 1:N){ Y[n] ~ normal(a[school[n]]+b[school[n]]*X[n],sig_st); } }
少し複雑に見えますが、一つずつ見ていけばそんなに難しくないかと思います。
さて、これをstratified3.stanとして保存します。(stratified2は前回使用したので...^ ^;)
Rのスクリプトファイルに戻り、stanを実行しましょう。ただし、dataを渡すときにprefだけは、学校数分の繰り返しになるので少し工夫が必要です。
pref <- as.numeric(unique(st_df[,c("school","pref")])$pref) > pref [1] 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 3 3 3 data <- list(N=450,P=3,K=18,X=st_df$X,Y=st_df$Y, pref = pref, school=as.numeric(st_df$school)) #結果に再現性を持たせるためseedを指定 stf3_model <- sampling(stratified3, data = data,seed=123)
無事に収束しました。それぞれのパラメーターの95%ベイズ信用区間を見てみます。
#結果の抜きだし stf3_res <- rstan::extract(stfw_model) data.frame(a0=stfw_res$a0,b0=stfw_res$b0, sig_ap=stfw_res$sig_ap,sig_bp=stfw_res$sig_bp, sig_a=stfw_res$sig_a,sig_b=stfw_res$sig_b, sig_st = stfw_res$sig_st) %>% apply(2,function(x){ c(mean=mean(x), quantile(x,prob=c(2.5,97.5)/100)) }) a0 b0 sig_ap sig_bp mean 126.8517 19.73688 285.47193 25.753912 2.5% -277.5858 -29.72325 30.84596 2.122254 97.5% 515.2349 58.55967 1521.18453 155.968886 sig_a sig_b sig_st mean 40.33493 8.300431 28.98467 2.5% 20.02583 5.752782 27.06487 97.5% 67.94399 12.132714 31.09704
a0、b0が回帰直線の全体平均、sigがバラツキになります。これを見ると学校ごとのバラツキ(sig_a,sig_b)が小さく、都道府県ごとのバラツキ(sig_ap,sig_bp)が大きいことが分かりますね。
今回の結果から、都道府県によって勉強時間と点数の関係が大きく異なり、同じ県内の学校間ではそれほど大きな違いはないことが推測されます。また、全体傾きの信用区間に負の値が含まれていることから、必ずしも勉強時間と点数は正の相関ではない可能性があることも分かります。
このように階層ベイズでは、パラメーターの確率分布から現象の解釈に幅を持たせることができます。
次に全体平均の回帰直線をグラフに書いてみましょう。
st_df %>% ggplot(aes(x=X,y=Y))+ geom_point(aes(col=pref),alpha = 0.5)+ geom_abline(data=data.frame(intercept=mean(stf3_res$a0), slope = mean(stf3_res$b0)), aes(intercept = intercept,slope=slope))
この直線の周りに都道府県ごとの回帰直線がバラツキつくことになります。

予測
さて、ここからは新たなデータに対しての予測を行ってみましょう。都道府県ごと、学校ごとの回帰直線全てに対して、予測ベイズ信用区間を求めることができるのですが、全部は大変なので都道府県2に属する学校15だけ抜き出して予測信用区間を求めてみます。
まず、学校15の勉強時間Xの最小値、最大値から新たなデータX_newを作ります。
X_new <- seq(min(st_df$X[st_df$school=="15"]), max(st_df$X[st_df$school=="15"]))
次にX_newと推定された学校15のパラメーターから予測値をサンプリングします。
学校ごとの切片や傾きは、行にサンプリング値、列にそれぞれの値が格納されたマトリックス形式になっているので、学校15は15列目に格納されています。
#それぞれの値がマトリックス形式になっている。(学校1,2,3の切片のサンプリング値) > stf3_res$a[,1:3] %>% head() iterations [,1] [,2] [,3] [1,] 55.37208 55.12283 50.22053 [2,] 87.79503 22.29490 103.51240 [3,] 75.74991 62.75150 70.80592 [4,] 60.37975 15.10782 104.81250 [5,] 62.28817 60.77793 127.05651 [6,] 95.12799 54.67800 125.49079 #値を格納するための入れ物 pred15 <- matrix(nrow=nrow(stf3_res$a),ncol=length(X_new)) #学校15の予測値をX_newの値ごとにサンプリングする。 for(i in 1:length(X_new)){ pred15[,i] <- rnorm(nrow(stf3_res$a), stf3_res$a[,15]+stf3_res$b[,15]*X_new[i], sd=stf3_res$sig_st ) }
最後にそれぞれのX_newごとの95%信用区間を求めて、グラフに反映します。
pred15 %>% apply(2,function(x){ c(mean=mean(x), quantile(x,prob=c(2.5,97.5)/100)) }) %>% t() %>% as.data.frame()-> pred15_95 #X_newの値ごとの平均値と95%信用区間ができている > pred15_95 %>% head() mean 2.5% 97.5% 1 732.9922 667.4620 799.5950 2 766.5547 700.7648 834.0489 3 798.9205 734.1107 865.5736 4 831.2969 766.5246 897.2985 5 865.4416 802.5495 928.0433 6 897.4370 832.5853 962.6337 #グラフ化 st_df %>% ggplot()+ geom_point(aes(x=X,y=Y),col="black",alpha=0.5)+ geom_point(data=st_df[st_df$school=="15",], aes(x=X,y=Y,col=school))+ geom_line(data=data.frame(X_new,pred15_95), aes(x=X_new,y=mean), linetype=2,col="red")+ geom_ribbon(data=data.frame(X_new,pred15_95), aes(x=X_new,ymin=pred15_95$`2.5%`,ymax=pred15_95$`97.5%`), alpha=0.2,fill="red")

いい感じで予測ができているようですね!
まとめ
今回は複雑な関係性にあるデータを、階層ベイズを用いて解析しました。
階層ベイズは予測もできますが、データ解釈の幅が広がるのが大きなメリットでしょう。前回のように超事前分布に特定の分布を指定すれば、前提とする仮定を組み込むこともできます。
自由なモデリングができるのが、線形モデルや線形混合モデルではできないところなので、是非活用していきたいです!
NGモデル
この記事を書くにあたってつまったところがあるので、参考までに紹介しておきます。
stanでサンプリングした時のことです。パラメーターの95%信用区間を表示させてみると...
a0 b0 sig_ap mean 21.56403 -8525520147 43.632704 2.5% -32.05218 -177384237128 1.593957 97.5% 70.32450 85548233926 189.857798 sig_bp sig_a sig_b sig_st mean 66885460435 125.07212 8.276447 29.02534 2.5% 1610507486 87.31994 5.653232 27.11701 97.5% 433077085660 178.51167 12.034586 30.93676
んん!?b0とsig_bpの桁が明らかにおかしい....。データセットを作り直してみたり、seed値をかえてみたりで、3時間ほど格闘した末に犯人を見つけました。stanファイルのmodelブロックの中が...
for(k in 1:K){ a[k] ~ normal(ap[pref[k]],sig_a); b[k] ~ normal(ap[pref[k]],sig_b); }
そうです。傾きb[k]のところがbpではなく、apになってます。
皆さんも収束がおかしい場合は、stanファイルを確認してみることをお勧めします。
※本記事は筆者が個人的に学んだことをまとめた記事なります。数学の記法や詳細な理論、筆者の勘違い等で誤りがあった際はご指摘頂けると幸いです。
参考
こちらの内容をアレンジして記事を書きました。これほどわかりやすくベイズモデリングを学べる書籍はほとんどないでしょう。

StanとRでベイズ統計モデリング (Wonderful R)
- 作者: 松浦健太郎,石田基広
- 出版社/メーカー: 共立出版
- 発売日: 2016/10/25
- メディア: 単行本
- この商品を含むブログ (10件) を見る
有名なみどりぼんです。 一般化線形モデルから、混合モデル、階層ベイズまでの繋がりを理解するのは、この本が一番だと思います。

データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)
- 作者: 久保拓弥
- 出版社/メーカー: 岩波書店
- 発売日: 2012/05/19
- メディア: 単行本
- 購入: 16人 クリック: 163回
- この商品を含むブログ (29件) を見る