回帰直線の求め方~最尤法、最小二乗法、期待損失~

今回は回帰分析で用いられる回帰直線について、よく知られている最小二乗法、最尤法に加えて、最近学んだ期待損失なるものを使って、求めていきたいと思います！

今回のお題

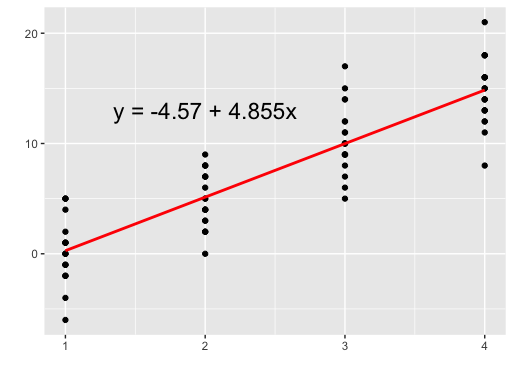
今回は以下のようなデータセットを使って、回帰直線を求めていきます。

 y1 <- round(rnorm(20,0,3))
 y2 <- round(rnorm(20,5,3))
 y3 <- round(rnorm(20,10,3))
 y4 <- round(rnorm(20,15,3))
 x <-  rep(seq(1,4),rep(20,4))
 df <- data.frame("x" = x,
                  "y" = c(y1,y2,y3,y4))
anslm <- lm(y~x,data = df)
Call:
lm(formula = y ~ x, data = df)

Coefficients:
(Intercept)            x  
     -4.575        4.855

f:id:h-wadsworth02:20181229185216p:plain:w400

最小二乗法

medi-data.hatenablog.com

まずは、有名な最小二乗法からやっていきます。最小二乗法とは、全ての点から回帰直線に引いた線の長さがもっとも短くなるように、回帰直線を求める方法になります。
グラフで表すと

f:id:h-wadsworth02:20181229185314p:plain

赤線の平均の長さを平均平方二乗誤差(Root Mean Square Error)といって、式で表すと

$\large RMSE = \sqrt{\dfrac{\sum_{i=1}^{n}(y_{i} - f(x_{i})^{2})}{N}}$

これを最小化する $f(x)$ が回帰直線になります。Rで実行すると

rmse <- function(para,y,x){
   a <- para[1]
   b <- para[2]
   (y - (a + b*x))^2 %>% 
     mean() %>% 
     sqrt()
 }
 df %$% 
   optim(c(1,1),mse,y=y,x=x)$par
[1] -4.575116  4.855185

うまくいきました！

最尤法

medi-data.hatenablog.com

続いて最尤法を使って求めてみます。今回は、全ての点が平均f(x)、分散 $\sigma^{2}$ の正規分布に従っていることを前提とします。グラフで見るとこんな感じです。 f:id:h-wadsworth02:20181229185543j:plain

この全てのxについての確率密度を掛け合わせた値（尤度）を最大化する方法が、最尤法になります。また、対数をとった対数尤度を最大化するのが一般的なので、これを式で表すと
$\log {\prod_{i = 1}^{n}\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(y_{i}-f(x_{i})^{2} }{ 2\sigma^{2}}\right\}} \\ = \sum_{i = 1}^{n}\log {\dfrac{1}{\sqrt{2\pi}\sigma}\exp\left\{-\dfrac{(y_{i}-f(x_{i})^{2} }{ 2\sigma^{2}}\right\}}\\ =-\dfrac{n}{2}\log (2\pi)-\dfrac{n}{2}\log (\sigma^{2})-\dfrac{1}{2\sigma^{2}}\sum_{i=1}^{n}(y_{i}-f(x_{i}))^{2}$

第一項は定数なので省略して、この対数尤度を最大化します！

>#上述の式通りに第二項以降を計算する関数を作成
log_like <- function(para,x,y){
   a <- para[1]
   b <- para[2]
   sigma <- para[3]
   ((-length(x)/2)*log(sigma^2))-((1/(2*sigma^2))*sum((y - (a + b*x))^2))
 }
#optimは最小化の関数なので、引数を与えて最大化させる
> optim(c(1,1,1),log_like,x = df$x , y=df$y,control =  list(fnscale=-1))$par
[1] -4.572675  4.854089  2.789027

おお出ました！標準偏差シグマも最初にデータを作成した時に3を設定したので、ほぼ同じ値になってます。

この最尤法の良いところは、最小二乗法と違って目的変数yがどんな分布であっても回帰分析ができることです！

期待損失

最後はあまり聞きなれない期待損失を使って求めてみます。期待損失とは、損失関数の期待値を最小にすることで求めることができます。式で表すと

$\large E(L) = \int\int \left\{y - f(x)\right\}^{2}p(x,y)dxdy$

なんだかすごそうな式ですね....。まず $\left\{y - f(x)\right\}^{2}$ の意味は、先ほどからよく出てくる二乗誤差ですね。そして、よくわからないのが $p(x,y)$ です。

これは同時確率を表していて、値xであるかつ値yである確率になります。それを全てのxとyについて積分、つまり足し合わせた値を最小にしろということになります。

ちなみに今回は $p(x,y)$ の分布が分からないので、ベイズの定理を使って

$\large p(x,y) = p(y\,|\,x)p(x)$

として求めました。（この辺にお詳しい方良い方法があれば教えて頂きたいです...）

実際にやってみましょう！

#値がxになる確率
px <- 1/4
#xがある値をとった際に、yがある値になる確率
 p_y_x <- function(h,i){nrow(filter(df,y==h,x ==i))/10}
#例：xが1だった場合にyの値が0になる確率は15%
p_y_x(0,1)
[1] 0.15

>#ベイズの定理から同時確率を求める
#同時確率とその時のx,yの値を格納するためのベクトル
pxy <- c()
x <- c()
y <- c()
for(i in unique(df$x)){
  for(h in unique(filter(df , x==i)$y)){
    pxy <- c(pxy,p_y_x(h,i)*px)
    x <- c(x,i)
    y <- c(y,h)
  }
}
> head(data.frame(x,y,pxy))
  x  y      pxy
1 1 -2 0.001875
2 1 -1 0.001875
3 1  5 0.001875
4 1  0 0.001875
5 1  1 0.002500
6 1 -4 0.000625

> #期待損失を定義
loss <- function(para,x,y,pxy){
   a <- para[1]
   b <- para[2]
  
   sum((y-(a+b*x))^2*pxy)
 }
>#最小化する
> optim(c(1,1),loss,x = x,y = y,pxy = pxy)$par
[1] -4.575116  4.855185

おお！うまく推定できました！同時確率を散布図にプロットしてみると、

f:id:h-wadsworth02:20181229190019p:plain

同時確率は元から分かっているので、確率が低い時に損失が大きくなるようにf(x)を決めていると言えますね！

ですが、この期待損失を使った求め方は、私も理解しきれていないので、どなたかご教授くださいm( )m

まとめ

今回は回帰分析のための3つの方法をまとめてみました。特に期待損失を使ったやり方は馴染みがなかったので、もし詳しい方がいればコメントください！

最後までお読み頂きありがとうございました！

参考

パターン認識と機械学習上

作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
出版社/メーカー: 丸善出版
発売日: 2012/04/05
メディア: 単行本（ソフトカバー）
購入: 6人クリック: 33回
この商品を含むブログ (20件) を見る

今回のRソースコード

library(ggplot2)
library(dplyr)
library(magrittr)
#データセット
set.seed(123)
y1 <- round(rnorm(20,0,3))
y2 <- round(rnorm(20,5,3))
y3 <- round(rnorm(20,10,3))
y4 <- round(rnorm(20,15,3))
x <-  rep(seq(1,4),rep(20,4))
df <- data.frame("x" = x,
                 "y" = c(y1,y2,y3,y4))

anslm <- lm(y~x,data = df)
#グラフ化
df %>% 
  ggplot(aes(x,y))+
  geom_point()+
  xlab("")+
  ylab("")+
  stat_smooth(method = "lm",se = F,col = "red")+
  annotate("text",
           label = paste0("y = ",round(anslm$coefficients[[1]],2)," + ",anslm$coefficients[[2]],"x"),
           x = 2,y=13,size = 6)

fx <- function(x){anslm$coefficients[[1]]+anslm$coefficients[[2]]*x}

#最小二乗法
df %>% 
  ggplot(aes(x,y))+
  geom_point()+
  xlab("")+
  ylab("")+
  stat_smooth(method = "lm",se = F,lwd = 0.5,col = "black")+
  geom_segment(aes(x=1,y=fx(1),
                   xend =1,yend=y1[1]),col = "red")+
  geom_segment(aes(x=2,y=fx(2),
                   xend =2,yend=y2[4]),col = "red")+
  geom_segment(aes(x=3,y=fx(3),
                   xend =3,yend=y3[5]),col = "red")

#RMSEを計算
rmse <- function(para,y,x){
  a <- para[1]
  b <- para[2]
  (y - (a + b*x))^2 %>% 
    mean() %>% 
    sqrt()
}
#最小化
df %$% 
  optim(c(1,1),mse,y=y,x=x)$par


#尤度
#対数尤度関数
log_like <- function(para,x,y){
  a <- para[1]
  b <- para[2]
  sigma <- para[3]
  ((-length(x)/2)*log(sigma^2))-((1/(2*sigma^2))*sum((y - (a + b*x))^2))
}
#対数尤度を最大化
optim(c(1,1,1),log_like,x = df$x , y=df$y,control =  list(fnscale=-1))$par

#期待損失の最小化
px <- 1/4
p_y_x <- function(h,i){nrow(filter(df,y==h,x ==i))/20}
pxy <- c()
x <- c()
y <- c()
for(i in unique(df$x)){
  for(h in unique(filter(df , x==i)$y)){
    pxy <- c(pxy,p_y_x(h,i)*px)
    x <- c(x,i)
    y <- c(y,h)
  }
}

loss <- function(para,x,y,pxy){
  a <- para[1]
  b <- para[2]
 
  sum((y-(a+b*x))^2*pxy)
}
optim(c(1,1),loss,x = x,y = y,pxy = pxy)$par

#同時確率をグラフ化
ggplot()+
xlab("")+
ylab("")+
stat_smooth(data = df,aes(x,y),method = "lm",se = F,col = "red")+
geom_text(aes(x=x, y=y, label=sprintf("%.2f",pxy*100)))