
確率分布とは?
確率分布とは、相対的な物事の起こりやすさを表したものになります。
森にはいろいろな大きさのうさぎがいます。その中で、うさぎの大きさと遭遇のしやすさをグラフにしました。小さいうさぎや、大きいうさぎと比べて、平均的なうさぎは2倍ぐらいは遭遇しやすいです。このように確率分布は、物事の起こりやすさを相対的に表します。
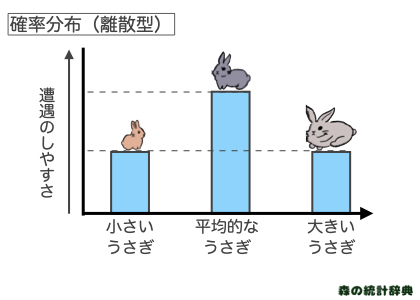
上の例のように、小さいうさぎ、平均的なうさぎ、大きいうさぎなどのカテゴリーになっている変数の確率分布を離散型確率分布と呼びます。
うさぎの大きさがカテゴリーではなく、20cm、21cm、21.1cm、、、と連続量になっている確率分布を連続型確率分布と呼びます。
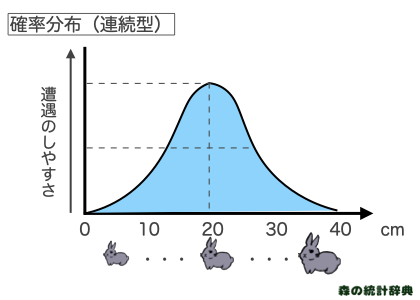
連続型でも解釈は同じで、相対的な起こりやすさを高さで表現します。 高さが連続的につながります。(詳しくは後述)
確率変数とは?
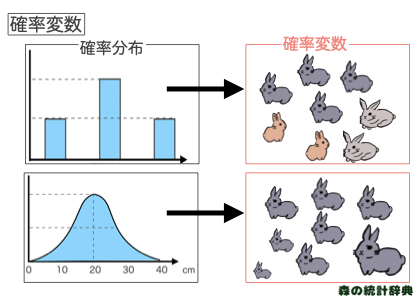
物事の起こりやすさを相対的に表したものが、確率分布でした。 その物事のことを確率変数と呼びます。
小さいうさぎ、平均的なうさぎ、大きいうさぎが、1つ目の確率分布の確率変数になりますし、うさぎの大きさ20cm、21cm、、が2つ目の確率分布の確率変数になります。
統計学では、確率変数は確率分布に従って得られると考えます。ややこしいですね。
例えば、平均的なうさぎと遭遇するという事象は、小さいうさぎと遭遇する事象に比べて、2倍ぐらい得られやすいです。
確率分布の特徴
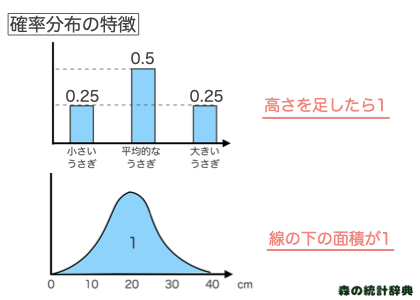
離散型確率分布の場合、確率分布のそれぞれの高さを足すと1になります。離散型確率分布では、確率分布の高さ=確率と解釈できます。
一方で連続型確率分布の場合は、確率分布の下の面積が1になります。(言い換えると、-∞から∞までを積分すると1になる。) 連続型では、確率分布の高さは、確率ではなく相対的な起こりやすさであることに注意してください。
連続型確率分布で高さが確率にならない理由は、ぴったりある値になる確率が分からないからです。
うさぎの大きさを精確に測定したとすると、20.146....cmのようになり、ぴったり20cmのうさぎと遭遇する確率は0になります。 しかし、-∞cm〜∞cmの大きさ範囲のうさぎと遭遇する確率は1ですよね。 (-∞cmなんてものは現実では考えられませんが、、)連続型確率分布の場合は、"○○〜○○cmのうさぎと遭遇する確率"のように、幅を決めることで確率を求めることができます。
まとめます
確率分布とは
- 相対的な物事の起こりやすさを表したもの
- 確率分布のそれぞれの高さを足すと1になる。(離散型確率分布)
- 確率分布の下の面積が1になる。(連続型確率分布)
確率変数とは
- 確率分布に従って得られる物事のこと
おすすめ参考書など
統計検定2級レベルまでを学ぶためのおすすめ参考書です。
※本記事は筆者が個人的に学んだこと感じたことをまとめた記事になります。所属する組織の意見・見解とは無関係です。


