有意水準と検出力をグラフィカルにシミュレーションで理解する

統計検定をする上でよく用いられるのは有意水準ですが、同時に検出力も考慮しなければなりません。

今回は有意水準と検出力についてまとめてみます。

有意水準、検出力とは？

第一種過誤（αエラー）、第二種過誤（βエラー）などとも呼ばれますが、簡単に言ってしまうと差がない時に差があるとする確率を有意水準（αなのであわてんぼうの過誤）、差がある時に差がないとする確率（βなのでぼんやりものの過誤）となります。

検出力は１ーβで表され、差がある時に差があるとする確率を表しています。

実際にやってみる

今回は対応のないt検定（等分散を仮定する場合とそうでない場合）の検定力をシミュレーションしていきます。

やり方としては、二標本を標本間の差を0~5に変化させてランダムサンプリングして、それぞれの検定結果をベクトルに格納します。

さらにその試行を1000回行なって、ベクトルをマトリックスに格納します。

最後にp値が0.05以下になった割合を求めて検出力を出します。

>#試行回数を1000回とする
> n <- 1000
>#p値を格納するための入れもの
> p1_values_mat <- matrix(ncol=6,nrow = n)
> p2_values_mat <- matrix(ncol=6,nrow = n)
> 
> for(j in 1:n){
   #p値を格納するための入れもの
   p1_values <- NULL
   p2_values <- NULL
   
   for(i in seq(0,5)){
     #二標本を標本間の差を0~5に変化させてランダムサンプリング
     a <- rnorm(10,10,6)
     b <- rnorm(10,10+i,2)
    
     p1 <- t.test(a,b,var.equal = F)$p.value
     p2 <- t.test(a,b,var.equal = T)$p.value
     
     p1_values[i+1]<- p1
     p2_values[i+1]<- p2
   }
   p1_values_mat[j,] <- p1_values
   p2_values_mat[j,] <- p2_values
 }
> #列にサンプル間の差0~5、行に試行回数としたp値の入ったマトリックス
> head(p1_values_mat,3)
          [,1]      [,2]         [,3]
[1,] 0.5860021 0.0153340 9.047196e-04
[2,] 0.5605508 0.1079923 4.545686e-04
[3,] 0.2163160 0.3866507 9.427683e-05
             [,4]         [,5]         [,6]
[1,] 3.948381e-07 4.133024e-12 7.640828e-09
[2,] 9.038200e-05 6.892034e-10 2.744553e-09
[3,] 5.919671e-05 1.266114e-12 6.375607e-08

> #有意差があった個数を試行回数の1000で割る
> p1_power <- apply(p1_values_mat <0.05,2,sum)/n
> p2_power <- apply(p2_values_mat <0.05,2,sum)/n
> 
> 
> #グラフ化
> plot(seq(0,5),p1_power,type ="b",col = "red",xlab ="",ylab="Power",ylim = c(0,1))
> points(seq(0,5),p2_power,type ="b",col = "blue")
> legend(x="topleft",legend = c("var.equal =F","var.equal =T"),
+        col =c("red","blue"),lty = 1)
> text(4,0.1,"N=10",cex=2)

>それぞれの検出力
> p1_power#等分散を仮定しない
[1] 0.056 0.083 0.154 0.284 0.400 0.648
> p2_power#等分散を仮定する
[1] 0.066 0.095 0.170 0.314 0.438 0.683

検出力は80%を基準にすることが多いのですが、サンプル数が10だと、差が5でも検出力が60~70%ぐらいであることが分かります。

また、今回は分散が異なるサンプルにしました。等分散を仮定するt検定では、検出力は高くなりますが、若干αエラーが大きいようです。（差が0の時も7%ぐらいの確率で差があるとしている）

等分散性の検定をしてから、どちらのt検定を行うかを決める方法もありますが、基本的には等分散を仮定しないt検定を使うことが最近は推奨されています！

次にサンプルサイズを変化させて、同じことを行なってみます。

> p1_power50
[1] 0.052 0.182 0.601 0.917 0.992 1.000
> p2_power50
[1] 0.053 0.183 0.604 0.918 0.992 1.000

> p1_power100
[1] 0.039 0.312 0.861 0.995 1.000 1.000
> p2_power100
[1] 0.039 0.316 0.862 0.995 1.000 1.000

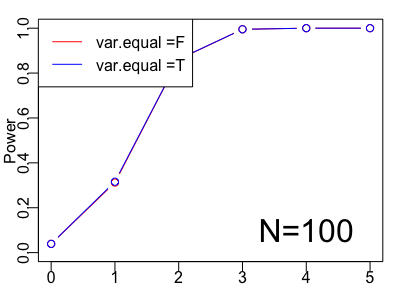
サンプルサイズが大きくなるとαエラーも小さくなり、サンプル間での差が小さくても検出力が高いことが分かります。

まとめ

今回はt検定の検出力をシミュレーションによって、確かめてみました。検出力は、サンプル間の差の大きさと、サンプル数、有意水準によって決まると言えそうです。

実は検出力を求める関数もあるのですが、このやり方を知っているとどんな検定の検出力も求めることができるので、知っておいて損はないですね！

参考

コードを書きながら読んでいくと、とても理解が深まります！

シミュレーションで理解する回帰分析 (Rで学ぶデータサイエンス 20)