事象の因果関係を見抜くためには、無作為介入が理想的ですが、世の中の多くはすでに存在するデータから因果関係が推論されます。
そんな既に観察されたデータ(観察データ)は、集計してみると関連性が見えてくることがありますが、短絡的に結果を解釈するととても危険です。
例えば、喫煙習慣と健康の関連を観察データから調べてみると、なんと喫煙習慣のある人の方が健康であるという結果が導き出されることもあります。
今回は、そんな危険性に立ち向かうための下準備として、観察データを解析する際に必ず確認すべき偏り(バイアス)について紹介していきます。
因果推論の基本的な考えはこちらです。
バイアスとは何か?
バイアスとは偏りという意味ですが、因果推論におけるバイアスとはなんでしょうか?
簡単な例を挙げてみます。スマホ広告とある商品の売り上げをデータから解析した時、スマホに広告が表示されているほど、その商品が売れていることがわかりました。しかし、その商品は若い人ほどよく買うものであった場合、若い人ほどスマホをみていることが想定されることから、スマホ広告と商品の売り上げにはなんの関係がなくても、一見関係があるように見えてしまいます。

このようにデータに偏りがあった場合(スマホの広告は若い人ほどよく表示されているなど)、本来は関係性がないところに因果関係を見出してしまたり、あるいは全く逆の因果関係を結論づけてしまったりします。
観察データから因果関係を推測する場合には、データに偏りがないことをしっかりと確認する必要があります。
それでは、観察データにはどのようなバイアスがあるのでしょうか?
交絡バイアス(confounding bias)
まずは一番わかりやすい交絡バイアスです。交絡バイアスは交絡因子によって引き起こされるバイアスです。交絡因子とは、推測したい要因にも結果にも作用する因子のことで、先ほどの例のように年齢はスマホ広告にも商品購買にも影響していることから、年齢という交絡因子によって交絡バイアスが生じています。

さらに、もう少し複雑な交絡バイアスについても考えてみます。例えば端末の性能が良いほどスマホがサクサク動き、より多くの広告が表示される、良い端末を持っているのは年収が高めの人で、その商品は高級嗜好品であったため年収が高い人ほど買いやすい、といった場合も交絡バイアスが引き起こされます。
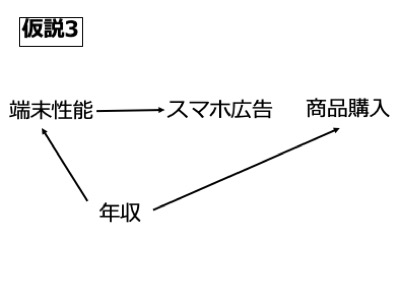
少しこじつけな感じもありますが、ここで言いたいのは、要因と結果の両方に作用しなくても、交絡因子となり得るということです。ここでは、端末機能はスマホ広告には影響していますが、商品購買には影響せず、年収は商品購買には影響していますが、スマホ広告には影響していません。しかし、関係のないスマホ広告と商品購買の間には、交絡バイアスによって見せかけの関係性が生じています。
これが交絡バイアスです。
選択バイアス(selection bias)
次はお店の新サービスと顧客満足度のアンケート調査結果から因果関係を推測してみましょう。これはよく用いられる調査方法だと思いますが、ここでもバイアスが生じる可能性があります。
例えば、今までと何も変わらないサービスに対して意見を求められても答えにくいですが、新サービスを受けた人ほどアンケートは答えやすいということはありえそうです。また、サービスに満足したため、気分がよくなってアンケートに答えるということもありそうです。
するとどうでしょうか?集めたアンケートは、実は新サービスを受けて満足した人の割合が必然的に多くなり、新サービスと顧客満足度との間に見せかけの関係が生まれてしまいます。

これが選択バイアスです。交絡因子と違うところは、特定の層のデータを選択した時のみバイアスを引き起こすところにあります。今回の例だとアンケートに答えた人のデータのみを選択したことで、バイアスが引き起こされています。アンケート結果に回答をしていない人のデータもあれば、新サービスと満足度との見せかけの関係性は出来ないわけです。(今回の場合は不可能ですが...)
これは最初に紹介したタバコを吸っている人ほど健康であるという関係が生まれるメカニズムでもあります。例えば調査をした人が高齢の人の集団であった場合、タバコによって害を受けやすい人はすでに亡くなっている可能性が高いです。また、健康状態が良い人ほど長生きするのは当たり前ですよね。
つまり、調査参加者は高齢になるまでタバコを吸い続けることができるほど健康であり、健康な喫煙者の割合が多くなる事で、タバコを吸うほど健康であるという全く逆の関連が生まれてしまうのです。(ちなみにこれをHealthy wokers effectと言います。)
バイアスの見つけ方
バイアスによって見せかけの関連性が引き起こされることはわかりましたが、バイアスはどのように見つければ良いのでしょうか?なんとかしてバイアスどもを発見したいところです。
その方法とは、自分たちの知識や経験を総動員することです。え?と思われた方はすみません。実はバイアスの見つけ方には決定的な方法なく、今までの知識と経験から、要因や結果に影響しそうな因子を特定するしかないのです。
しかし、因子間の関連をわかりやすくするツールはあります。それが先ほどから書いている矢印で結ばれた図、名前を有効巡回グラフ、またの名をDAGs(directed acyclic graphs)と言います。
DAGsの書き方のルールはいたって簡単で、変数の関係性を推測される因果関係の向きに合わせて矢印で繋ぐだけです。そして、二変数以上から影響を受けていない場合は交絡バイアスを引き起こす因子となる可能性があり、二変数以上から影響を受けている場合は選択バイアスを引き起こす因子となります。そして、DAGsの中では、変数間の流れが繋がった時に見せかけの関係性が生じます。
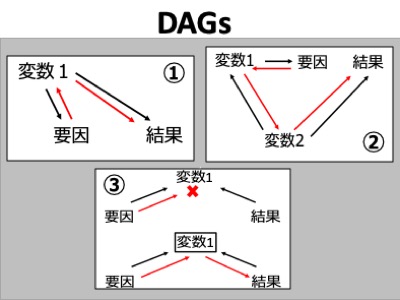
基本的なDAGsを上の図にまとめてみました。まず①ですが、これは年齢がスマホ広告と商品購入の交絡因子になるパターンと同じです。交絡因子は変数間に流れを作ります。どういうことかというと、変数1が交絡因子となることで、要因→変数1→結果と繋がり、交絡バイアスが生じます。②のパターンは年収と端末機能のパターンです。こちらも要因→変数1→変数2→結果と繋がるため、交絡バイアスが生じます。
③は選択バイアスのパターンです。変数1は要因と結果の両方から影響を受けています。この変数1のような変数をcollider(日本語では衝突器もしくは合流点)と呼びます。名前はどうでも良いのですが、大事なことはcolliderは何もしなければ上の図のように流れはできず、バイアスは引き起こしません。
しかし、このcolliderはアンケートに答えた人のデータしかないなど、条件を制限されることで選択バイアスとなります。DAGsでは条件付けをした変数という意味で、四角で変数を囲います。
これらのように、交絡バイアスや選択バイアスによってDAGsの流れができることを、バックドアパス(Back door pass)が開くと言います。このパスがが開いているかどうかで、データのバイアスを見つけることができるのです。
さて、このDAGsは一見面倒に思えます。実際私も初めてこれをみた時は全く必要性がわかりませんでした。
しかし!
観察データからバイアスを排除する方法については、回帰分析や層別化など様々な方法がありますが、その調整すべき変数を特定するためにも変数間の関係性を見極めなければ、致命的な誤解釈を招くことになります。例えば、colliderを誤って調整してしまった場合には、選択バイアスを引き起こします。
複雑なこの世界において、DAGsはとても強力なツールとなるのです。
具体的な交絡因子などの排除法はまた次回まとめていきます。
まとめ
因果推論において、データのバイアスはとても重要な要素です。世の中の因果関係というのは、とてもとても複雑で、出来るだけ真実に近い関係性を見出すには、全てのデータを疑うぐらいの思慮深さが必要そうですね。
じゃあどうやって、交絡因子と戦うの?という内容については次回まとめていきます。
※本記事は筆者が個人的に学んだことをまとめた記事なります。数学の記法や詳細な理論、筆者の勘違い等で誤りがあった際はご指摘頂けると幸いです。
参考
有効巡回グラフについては以下の書籍にも書いてあります。理論的な背景までしっかりとまとまっていますので、詳しい理論が知りたい方にはオススメです。

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)
- 作者: 星野崇宏
- 出版社/メーカー: 岩波書店
- 発売日: 2009/07/29
- メディア: 単行本
- 購入: 29人 クリック: 285回
- この商品を含むブログ (26件) を見る
ハバード大学が無料で公開している因果推論に関するテキストです。RやPythonのコードもあり、これが無料で読めるとは本当にすごいです。本記事の内容もこちらを参考にしています。
https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/
因果推論に関して、おそらく日本で一分かりやすく、しかも丁寧に解説されているブログです。大変参考にさせて頂いてます。