マルチレベル分析の基礎〜結果の解釈と応用編〜 - 医療職からデータサイエンティストへ

前回は、テストの点数と勉強時間との関連を学校レベルと個人レベルに分けて解析するマルチレベル分析の基礎をまとめました。

今回は、より現実の背景を反映させてさらに解釈の幅を広げていきます！ Rを実践する場合は前回のデータセットをそのまま使うので、こちらの記事を参考にデータを作成してください。

www.medi-08-data-06.work

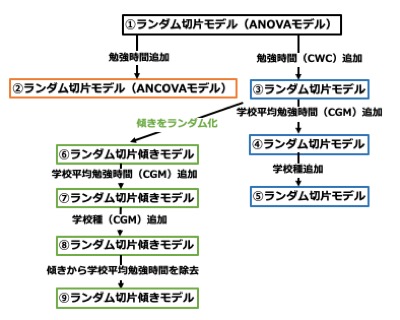
ランダム切片傾きモデルとは？

さて、前回のランダム切片モデルでは、7つの学校全てで傾きが等しい、つまり勉強時間とテストの点数との関係が同じであると仮定しました。

f:id:h-wadsworth02:20190211182521j:plain

しかし、現実では勉強時間と点数の関係は学校ごとで異なることが考えられます。例えば、平均的にテストの点数が高い学校は、伸びしろが少ないため傾きが小さかったり....

その背景をモデルに反映させて、学校ごとで切片も傾きも異なるとする方法をランダム切片傾きモデルと呼びます。

線形混合モデル

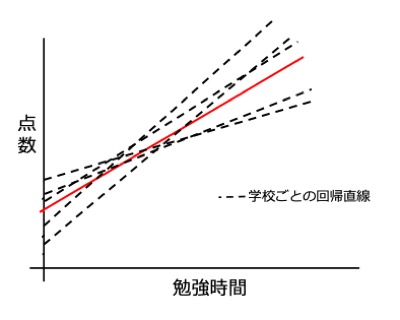
これを使うと、交互作用の影響、例えば学校の勉強時間平均点や学校種などの学校レベル変数が、個人の勉強時間と点数の関連に与える影響なども検討することができるようになります！

ランダム切片傾きモデルの実践

実際にランダム切片傾きモデルをモデリングしていきましょう。ここでは、新たに以下の疑問を考えます。

学校よって勉強時間と点数の関連は異なるのか
テストの学校平均は、個人の勉強時間と点数の関連に影響するか
学校の種類（公立、私立）は、個人の勉強時間と点数の関連に影響するか

まずは一つ目の疑問です。これを議論するために傾きにもランダム効果を導入し、その傾きの分散が有意であれば学校によって個人の勉強時間と点数の関連が異なると言えます。

式は、

$Y_{st} = a_{sc} +b_{sc}*(X_{st}-\bar{X_{sc}}) + \epsilon\\ a_{sc} = a0 + \epsilon_{a}\\ b_{sc} = b0 + \epsilon_{b}$

$\epsilon \sim Normal(0\,, \sigma^{2})\\ \epsilon_{a} \sim Normal (0 \,, \sigma_{asc}^{2})\\ \epsilon_{b} \sim Normal (0 \,, \sigma_{bsc}^{2})$

$Y_{st}\,:\,生徒の点数\\ X_{st}\,:\,生徒の勉強時間\\ \bar{X_{sc}}\,:\,学校ごとの平均勉強時間\\ a_{sc}\,:\,学校ごとの切片\\ b_{sc}\,:\,学校ごとの傾き\\ \sigma^{2}\,:\,誤差の分散(学校内分散)\\ a0\,:\,切片平均\\ \sigma_{asc}^{2}\,:\,a_{sc}の分散(学校間切片分散)\\ b0\,:\, 傾き平均（勉強時間の点数への影響）\\ \sigma_{bsc}^{2}\,:\,b_{sc}の分散(学校間傾き分散)$

となります。個人レベルで勉強時間と点数の関連をみたいので勉強時間はCWC（集団平均中心化）を行なっています。

これを求めてみると

$\sigma^{2}\,:\,10943\\ a0\,:\,1617\\ \sigma_{asc}^{2}\,:\,100693\\ b0\,:\, 14\\ \sigma_{bsc}^{2}\,:\, 100$

となります。傾き平均が14、傾き分散が98.6なので

個人でみると平均的に勉強時間が1時間長いと点数が14点高くなるが、その関係は学校によって異なり、14±10(100の平方根)ぐらいの幅がある

という解釈になります。学校によって勉強時間と点数の関連は異なると言えそうです。

Rでは以下のように実行します。

st_df2 %>% 
  lme4::lmer(data=.,Y~X_cwc+(1+X_cwc|school),REML = F) %>% 
  summary()

Linear mixed model fit by maximum likelihood [lmerMod]
Formula: Y ~ X_cwc + (1 + X_cwc | school)
   Data: .

     AIC      BIC   logLik deviance df.resid 
  1388.7   1404.9   -688.3   1376.7      104 

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.36089 -0.66215 -0.08028  0.71928  2.46437 

Random effects:
 Groups   Name        Variance Std.Dev. Corr
 school   (Intercept) 100693.5 317.32       
          X_cwc           98.6   9.93   0.83
 Residual              10943.4 104.61       
Number of obs: 110, groups:  school, 7

Fixed effects:
            Estimate Std. Error t value
(Intercept)  1617.67     120.61  13.412
X_cwc          14.68       4.11   3.572

Correlation of Fixed Effects:
      (Intr)
X_cwc 0.760

交互作用の考え方

解析を進めます。ここでは、ランダム切片モデルと同じように学校レベルの変数（勉強時間の学校平均と学校種）を傾きにも加えます。

するとこのモデルの解釈としては、学校レベルの変数が個人レベルの傾きに与える影響と解釈でき、学校レベルの変数と個人レベルの変数の交互作用になります。

まずは勉強時間の学校平均を加えたモデルを作ってみましょう。学校平均はCGM（全体平均中心化）を行なっておきます。（全体平均中心化を行う理由について記事下で補足しました）

$Y_{st} = a_{sc} +b_{sc}*(X_{st}-\bar{X_{sc}}) + \epsilon \\ a_{sc} = a0 + ab_{1} * (\bar{X_{sc}} - \bar{X_{st}})+\epsilon_{a}\\ b_{sc} = b0 + b_{1} * (\bar{X_{sc}} - \bar{X_{st}})+\epsilon_{b}$

$\epsilon \sim Normal(0\,, \sigma^{2})\\ \epsilon_{a} \sim Normal (0 \,, \sigma_{asc}^{2})\\ \epsilon_{b} \sim Normal (0 \,, \sigma_{bsc}^{2})$

$Y_{st}\,:\,生徒の点数\\ X_{st}\,:\,生徒の勉強時間\\ \bar{X_{sc}}\,:\,学校ごとの平均勉強時間\\ \bar{X}_{st}\,:\,勉強時間の全体平均\\ a_{sc}\,:\,学校ごとの切片\\ b_{sc}\,:\,学校ごとの傾き\\ \sigma^{2}\,:\,誤差の分散(学校内分散)\\ a0\,:\,切片平均\\ ab_{1}\,:\,学校レベルでの勉強時間の点数への影響\\ \sigma_{asc}^{2}\,:\,a_{sc}の分散(学校間切片分散)\\ b0\,:\, 傾き平均（勉強時間の点数への影響）\\ b_{1}\,:\,学校平均が個人の傾きに与える影響（交互作用）\\ \sigma_{bsc}^{2}\,:\,b_{sc}の分散(学校間傾き分散)$

だいぶパラメーターが増えてきましたが、一つづつゆっくり見ていけば理解できるかと思います。

これを求めると

$\sigma^{2}\,:\,10934\\ a0\,:\,1595\\ ab_{1}\,:\, 26\\ \sigma_{asc}^{2}\,:\, 11400\\ b0\,:\, 14\\ b_{1}\,:\,0.7(SE=0.2)\\ \sigma_{bsc}^{2}\,:\,27$

さて、 $b_{1}$ をみてみると傾き0.7、標準誤差0.2で有意な傾きとなっています。つまり、学校平均が1時間長い学校にいる生徒は、1時間勉強時間が長くなると点数が14+0.7=14.7点高くなると言えます。

先ほど学校によって勉強時間と点数の関連が10点ほど異なっていると解析されましたが、それは学校の平均勉強時間が影響していたようです。その証拠に傾きのバラツキである $\sigma_{bsc}^{2}$ が100から27まで小さくなっています。

Rでは以下のように実行します。

#交互作用項は:で表す
st_df3 %>% 
  lme4::lmer(data=.,Y~X_cwc+X_sc_cgm+X_cwc:X_sc_cgm+(1+X_cwc|school),REML = F) %>% 
  summary()

Linear mixed model fit by maximum likelihood  ['lmerMod']
Formula: Y ~ X_cwc + X_sc_cgm + X_cwc:X_sc_cgm + (1 + X_cwc | school)
   Data: .

     AIC      BIC   logLik deviance df.resid 
  1377.4   1399.0   -680.7   1361.4      102 

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-2.36309 -0.63390 -0.09406  0.74578  2.35041 

Random effects:
 Groups   Name        Variance Std.Dev. Corr
 school   (Intercept) 11400.45 106.773      
          X_cwc          27.32   5.227  0.13
 Residual             10934.69 104.569      
Number of obs: 110, groups:  school, 7

Fixed effects:
                Estimate Std. Error t value
(Intercept)    1595.0125    42.4096  37.610
X_cwc            14.1995     2.5730   5.519
X_sc_cgm         25.6515     3.6352   7.056
X_cwc:X_sc_cgm    0.7142     0.2161   3.306

Correlation of Fixed Effects:
            (Intr) X_cwc  X_sc_c
X_cwc        0.101              
X_sc_cgm    -0.083 -0.008       
X_cwc:X_sc_ -0.008 -0.062  0.102

続いて、学校種が個人の勉強時間と点数に与える影響（学校種と点数の交互作用）も加えてみましょう。学校種は公立（0）、私立（1）のニ値ですが、これも全体平均中心化を行います。

$Y_{st} = a_{sc} +b_{sc}*(X_{st}-\bar{X_{sc}}) + \epsilon \\ a_{sc} = a0 + ab_{1} * (\bar{X_{sc}} - \bar{X_{st}})+ab_{2} * (SCtype-\bar{SCtype})+\epsilon_{a}\\ b_{sc} = b0 + b_{1} * (\bar{X_{sc}} - \bar{X_{st}})+b_{2} * (SCtype-\bar{SCtype})+\epsilon_{b}$

$\epsilon \sim Normal(0\,, \sigma^{2})\\ \epsilon_{a} \sim Normal (0 \,, \sigma_{asc}^{2})\\ \epsilon_{b} \sim Normal (0 \,, \sigma_{bsc}^{2})$

$Y_{st}\,:\,生徒の点数\\ X_{st}\,:\,生徒の勉強時間\\ \bar{X_{sc}}\,:\,学校ごとの平均勉強時間\\ \bar{X}_{st}\,:\,勉強時間の全体平均\\ SCtype\,:\,学校種（公立:0,私立:1）\\ \bar{SCtype}\,:\,学校種の全体平均\\ a_{sc}\,:\,学校ごとの切片\\ b_{sc}\,:\,学校ごとの傾き\\ \sigma^{2}\,:\,誤差の分散(学校内分散)\\ a0\,:\,切片平均\\ ab_{1}\,:\,学校レベルでの勉強時間の点数への影響\\ ab_{2}\,:\,学校種の勉強時間の点数への影響\\ \sigma_{asc}^{2}\,:\,a_{sc}の分散(学校間切片分散)\\ b0\,:\, 傾き平均（勉強時間の点数への影響）\\ b_{1}\,:\,学校平均が個人の傾きに与える影響（交互作用）\\ b_{2}\,:\,学校種が個人の傾きに与える影響（交互作用）\\ \sigma_{bsc}^{2}\,:\,b_{sc}の分散(学校間傾き分散)$

これを求めると

$\sigma^{2}\,:\,10842\\ a0\,:\,1587\\ ab_{1}\,:\,23\\ ab_{2}\,:\, 73\\ \sigma_{asc}^{2}\,:\,10950\\ b0\,:\, 14\\ b_{1}\,:\,-0.3(SE=0.5)\\ b_{2}\,:\,27(SE=13)\\ \sigma_{bsc}^{2}\,:\, 22$

$b_{2}$ は27点になりました。これは、公立に比べて私立にいる生徒が1時間勉強時間が長くなると点数が17+27=44点高くなるということを表します。しかし、標準誤差も13点と大きいため、この関係は完全に成り立つ訳ではなさそうでうす。

逆に $b_{1}$ は-0.3ですが有意な傾きではなくなりました。

傾き分散をみてみると4.6点（22の平方根）となっていて一番小さくなっています。つまり、学校間での傾きの違いは、完全に有意ではないにしろ学校種の影響が大きそうだと推測できます。

Rの実行

#sctypeの中心化
st_df3 %>% 
  mutate(sctype_cgm = sctype-mean(sctype))->st_df4

#実行
st_df4 %>% 
  lme4::lmer(data=.,Y~X_cwc+X_sc_cgm+sctype_cgm+(X_cwc:sctype_cgm)+(X_cwc:X_sc_cgm)+(1+X_cwc|school),REML = F) %>% 
  summary()

Linear mixed model fit by maximum likelihood  ['lmerMod']
Formula: 
Y ~ X_cwc * X_sc_cgm + X_cwc * sctype_cgm + (1 + X_cwc | school)
   Data: .

     AIC      BIC   logLik deviance df.resid 
  1378.3   1405.3   -679.2   1358.3      100 

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-2.4104 -0.6227 -0.1070  0.7558  2.3087 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 school   (Intercept) 10950.10 104.643       
          X_cwc          21.83   4.672  -0.52
 Residual             10842.79 104.129       
Number of obs: 110, groups:  school, 7

Fixed effects:
                  Estimate Std. Error t value
(Intercept)      1587.0886    47.3350  33.529
X_cwc              13.5177     2.4240   5.577
X_sc_cgm           22.7491     8.6134   2.641
sctype_cgm         73.1461   202.7909   0.361
X_cwc:X_sc_cgm     -0.2631     0.5312  -0.495
X_cwc:sctype_cgm   25.6401    13.2397   1.937

Correlation of Fixed Effects:
            (Intr) X_cwc  X_sc_c sctyp_ X_:X__
X_cwc       -0.435                            
X_sc_cgm     0.403 -0.182                     
sctype_cgm  -0.476  0.215 -0.910              
X_cwc:X_sc_ -0.153  0.180 -0.350  0.320       
X_cwc:scty_  0.171 -0.214  0.302 -0.333 -0.927

先ほどのモデルから傾きへの影響は学校種による違いが大きいことが分かりました。そこで、最後に学校平均を学校レベルの傾きから抜いてみましょう。

$\epsilon \sim Normal(0\,, \sigma^{2})\\ \epsilon_{a} \sim Normal (0 \,, \sigma_{asc}^{2})\\ \epsilon_{b} \sim Normal (0 \,, \sigma_{bsc}^{2})$

$Y_{st}\,:\,生徒の点数\\ X_{st}\,:\,生徒の勉強時間\\ \bar{X_{sc}}\,:\,学校ごとの平均勉強時間\\ \bar{X}_{st}\,:\,勉強時間の全体平均\\ SCtype\,:\,学校種（公立:0,私立:1）\\ \bar{SCtype}\,:\,学校種の全体平均\\ a_{sc}\,:\,学校ごとの切片\\ b_{sc}\,:\,学校ごとの傾き\\ \sigma^{2}\,:\,誤差の分散(学校内分散)\\ a0\,:\,切片平均\\ ab_{1}\,:\,学校レベルでの勉強時間の点数への影響\\ ab_{2}\,:\,学校種の勉強時間の点数への影響\\ \sigma_{asc}^{2}\,:\,a_{sc}の分散(学校間切片分散)\\ b0\,:\, 傾き平均（勉強時間の点数への影響）\\ b_{2}\,:\,学校種が個人の傾きに与える影響（交互作用）\\ \sigma_{bsc}^{2}\,:\,b_{sc}の分散(学校間傾き分散)$

これを求めると

$\sigma^{2}\,:\,10839\\ a0\,:\,1584\\ ab_{1}\,:\,23\\ ab_{2}\,:\, 93 \\ \sigma_{asc}^{2}\,:\, 1584\\ b0\,:\, 14\\ b_{2}\,:\,19(SE=4.9) \\ \sigma_{bsc}^{2}\,:\,20$

$b_{2}$ が傾き19、標準誤差4.9で有意な傾きとなりました。ここから、勉強時間学校平均によって説明されていた傾きの分散がなくなったため、学校種の影響が明確になったと言えそうです。傾き分散 $\sigma_{bsc}$ も4.5点(20の平方根)と今までで一番小さくなりました。

Rの実行

st_df4 %>% 
  lme4::lmer(data=.,Y~X_cwc+X_sc_cgm+sctype_cgm+(X_cwc:X_sc_cgm)+(1+X_cwc|school),REML = F) %>% 
  summary()

Linear mixed model fit by maximum likelihood  ['lmerMod']
Formula: 
Y ~ X_cwc + X_sc_cgm + X_cwc * sctype_cgm + (1 + X_cwc | school)
   Data: .

     AIC      BIC   logLik deviance df.resid 
  1376.5   1400.8   -679.3   1358.5      101 

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-2.4010 -0.6278 -0.1124  0.7503  2.3070 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 school   (Intercept) 10988.76 104.827       
          X_cwc          20.48   4.525  -0.41
 Residual             10838.79 104.110       
Number of obs: 110, groups:  school, 7

Fixed effects:
                 Estimate Std. Error t value
(Intercept)      1584.645     47.085  33.655
X_cwc              13.633      2.337   5.833
X_sc_cgm           21.813      8.309   2.625
sctype_cgm         93.709    196.894   0.476
X_cwc:sctype_cgm   19.477      4.888   3.984

Correlation of Fixed Effects:
            (Intr) X_cwc  X_sc_c sctyp_
X_cwc       -0.324                     
X_sc_cgm     0.389 -0.101              
sctype_cgm  -0.465  0.130 -0.904       
X_cwc:scty_  0.059 -0.126 -0.051 -0.074

モデルのまとめ

ここで今までのモデルの関係性とそのパラメーターを比較してみましょう。

線形混合モデル

Param	1	2	3	4	5	6	7	8	9
$\sigma^{2}$	28116	16318	16278	16297	16315	10943	10934	10842	10838
$\sigma_{asc}^{2}$	98742	33510	99957	10723	10247	100693	11400	10950	10988
$\sigma_{bsc}^{2}$	-	-	-	-	-	99	27	22	20
$a0$	1618	1172	1617	1596	87	1618	1595	1587	1584
$ab_{1}$	-	-	-	26(SE=3.7)	23 (SE=8.6)	-	26 (SE=3.7)	23 (SE=8.6)	21 (SE=8.3)
$ab_{2}$	-	-	-	-	83 (SE=201.8)	-	-	73 (SE=202.8)	94 (SE=196.9)
$b0$	-	13 (SE=1.4)	12(SE=1.4)	12(SE=1.4)	12 (SE=1.4)	15 (SE=4)	14 (SE=2.6)	14 (SE=2.4)	14 (SE=2.3)
$b_{1}$	-	-	-	-	-	-	0.7(SE=0.2)	-0.3 (SE= 0.5)	-
$b_{2}$	-	-	-	-	-	-	-	26 (SE=13.2)	19.5 (SE=4.9)

上の表から個人の点数バラツキを示す $\sigma$ はモデル9が一番小さく、当てはまりが良いことがわかります。このモデル9とこれまでの解析から以下のような解釈ができます。

個人の勉強時間が1時間長いと点数は平均的に $b0 = 14$ 点高くなる。しかし、学校種によって傾きが異なり、私立の学校に属する生徒は勉強時間が1時間長いと点数は平均的に $b0+b_{2} = 14+19.5 = 33.5$ 点高くなる。また、学校間で比べた時には同じ勉強時間でも点数が異なる。例えばA学校に属する生徒に比べ、A学校より勉強時間学校平均が1時間長いB学校に属する生徒の点数は、平均的に $ab_{1}=21$ 点高くなる。

このようにマルチレベル分析では、集団レベルと個人レベルの両方でモデルを解釈することができます。今回は個人レベルの変数が勉強時間のみであったため、個人レベルの傾き推定値が14点前後で変化がありませんでした。ここに個人レベルの変数（性別等）を加えるとより深いモデリングとなり、例えば性別の影響を調整しても勉強時間と点数に関連はあるのか？といった解釈もできます。

まとめ

今回は、傾きにもランダム性を想定した線形混合モデルの中のランダム切片傾きモデルを扱いました。

今回のように現象の解釈には機械学習よりも統計モデリングの方が適しています。マルチレベル分析は目的変数や説明変数の設定法によって解釈の仕方が大きく変わるので、目的に合わせたモデリングができると良いですね！

---補足：学校レベルの説明変数を全体平均中心化する理由---

全体平均中心化は、全ての変数から同じ値を引くので変数間の関連は変わりません。ではなぜCGMが推奨されているのでしょう？それは、今回のようなランダム切片傾きモデルの場合は、個人レベルと集団レベルの変数の交互作用が登場します。もし、CGMを行わない場合は交互作用項と個人レベルの変数（今回は勉強時間）の相関が高くなり、多重共線性が生じるためです。

例えばモデル7の場合は以下のようなモデルでした。()

$Y_{st} = a_{sc} +b_{sc}*X_{cwc} + \epsilon \\ a_{sc} = a0 + ab_{1} * X_{sc_{cgm}}+\epsilon_{a}\\ b_{sc} = b0 + b_{1} * X_{sc_{cgm}} +\epsilon_{b}$

この式を一つにしてみると

$Y_{st} = (a0 + ab_{1} * X_{sc_{cgm}}+\epsilon_{a})+(b0 + b_{1} * X_{sc_{cgm}} +\epsilon_{b}) * X_{cwc} + \epsilon \\ =a0 + ab_{1} * X_{sc_{cgm}}+ b0 * X_{cwc}+ b_{1} * X_{sc_{cgm}} * X_{cwc}+(\epsilon_{a}+\epsilon_{b}*X_{cwc}+ \epsilon)$

となってこれは、3つの変数 $X_{sc_{cgm}},X_{cwc},X_{sc_{cgm}} * X_{cwc}$ の重回帰分析と等しくなります。この時 $X_{sc_{cgm}}$ を中心化しない場合（ $X_{sc}$ とする)は、 $X_{cwc}$ と $X_{cwc} * X_{sc}$ の間で高い相関関係になり多重共線性が生じてしまいます。これが、集団レベルの変数を全体平均中心化する理由になります。